本文主要是介绍系数矩阵的行压缩存储(CSR/CRS), 列压缩存储CCS,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
转载地址:http://blog.csdn.net/bigpiglet_zju/article/details/20791881
稀疏矩阵(Sparse Matrix)由于有很多0,为了节省空间,一般压缩存储。通常只需要保存非零元素及其位置即可。
下面介绍Compressed Row Storage(CRS)格式或者称为 Compressed sparse row(CSR)格式,由名称可见,该格式是把行的信息压缩存储了,只显式保留每行第一个非零元素的位置,具体在例子中可以看到。
假设有稀疏矩阵A,我们需要创建三个数组,一个浮点型数组val,另外两个为整型数组(col_ind, row_ptr)。
val数组,大小为矩阵A的非零元素的个数,保存矩阵A的非零元素(按从上往下,从左往右的行遍历方式访问元素)。
col_ind数组,和val数组一样,大小为矩阵A的非零元素的个数,保存val数组中元素的列索引。其数学表示为:
row_ptr数组,大小为矩阵A的行数,保存矩阵A的每行第一个非零元素在val中的索引。其数学表示为:
按照惯例,一般定义row_ptr(n+1) = nnz + 1,而nnz是A中非零元素的个数。
该方法可以节省很多空间,只需要2nnz + n + 1个存储单元,而不是n的平方个单元。
//ps:这的n好像指的是:方阵的行/列
看一个例子:
矩阵A定义为
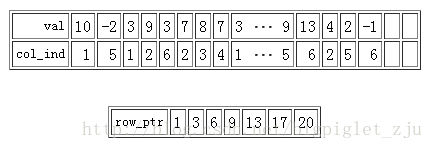
其CSR格式由三个数组定义为:
注意其中row_ptr数组的最后一个元素为20(19+1),因为矩阵A的非零元素为19。
Compressed Column Storage
Analogous to CRS, there is compressed column storage (CCS), which is also called the Harwell-Boeing sparse matrix format [139]. The CCS format is identical to the CRS format except that the columns of ![]() are stored (traversed) instead of the rows. In other words, the CCS format is the CRS format for
are stored (traversed) instead of the rows. In other words, the CCS format is the CRS format for ![]() .
.
The CCS format is specified by the ![]() arrays {val, row_ind, col_ptr}, where row_ind stores the row indices of each nonzero, and col_ptr stores the index of the elements in val which start a column of
arrays {val, row_ind, col_ptr}, where row_ind stores the row indices of each nonzero, and col_ptr stores the index of the elements in val which start a column of ![]() . The CCS format for the matrix
. The CCS format for the matrix ![]() in (10.1) is given by
in (10.1) is given by
| val | 10 | 3 | 3 | 9 | 7 | 8 | 4 | 8 | 8 | 2 | 3 | 13 | -1 | ||
| row_ind | 1 | 2 | 4 | 2 | 3 | 5 | 6 | 3 | 4 | 6 | 2 | 5 | 6 |
| col_ptr | 1 | 4 | 8 | 10 | 13 | 17 | 20 |
参考:
1. Compressed Row Storage
http://web.eecs.utk.edu/~dongarra/etemplates/node373.html
2. Compressed Column Storage
http://www.netlib.org/utk/people/JackDongarra/etemplates/node374.html
3. Sparse Matrix Compression Formats
http://www.cs.colostate.edu/~mroberts/toolbox/c++/sparseMatrix/sparse_matrix_compression.html
这篇关于系数矩阵的行压缩存储(CSR/CRS), 列压缩存储CCS的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!