本文主要是介绍【点云处理之论文狂读前沿版1】——Rethinking Network Design and Local Geometry in Point Cloud: A Simple Residual MLP,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
重新审视点云处理中的网络设计和局部几何结构——一个简单的残差MLP框架
- 1.摘要
- 2.引言
- 2.相关工作
- 3.方法
- 3.1 Revisiting point-based methods
- 3.2 PointMLP的框架结构
- 3.3 Geometric Affine Module
- 3.4 计算复杂度和Elite版
- 4.实验
- 4.1 Shape classification on ModelNet
- 4.2 Shape classification on ScanObjectNN
- 4.3 消融实验
- 4.4 Part segmentation
- 5.结论
- 6. 附录
- 6.1 PointMLP detail
- 6.2 Experiment setting detail
- 6.3 More detialed ablation studies
- 6.4 PointMLP depth
- 论文写作亮点
1.摘要
- 点云的局部几何结构可能并不是点云处理的关键。
- 提出了一个基于纯残差的MLP网络——PointMLP。
- 网络不考虑点云的局部信息,结构简单,推理速度更快,性能更好。
- 搭配一个轻量版的几何放射模块(geometric affine module),效果更佳。
- 代码地址:https://github.com/ma-xu/pointMLP-pytorch
2.引言
- 点云的特性:无序性、不规则性、稀疏性、敏感性
- 点云的应用:分类、语义分割、目标检测
- 之前对于点云的局部几何结构提取已经做的够好了,我们应该反过头来看看局部几何结构到底有没有必要考虑,网络上有没有什么可以改变的?
- 本文只用基于残差的MLP网络,其他啥也不用。
- 如果再加上local geometric affine module,自适应地对特征进行变换,那就更好啦。
- 我们提出的PointMLP又简单,效果又好,不信你看下图。


2.相关工作
点云分析
- Voxels & image
- Original point cloud
局部几何结构
- convolution-based methods (PointConv/2019, PAConv/2021)
- graph-based methods (DGCNN/2019, 3D-GCN/2021)
- attention-based methods(PCT, Point Transformer)
适用于点云的深度网络框架
就在最近,由于简洁MLP结构的高效和可扩展性,受到了很多地关注,因此,我们不再盲目跟风。
3.方法
feed-forward residual MLP network + geometric affine module
3.1 Revisiting point-based methods
给定一组点云 P = { p i ∣ i = 1 , ⋯ , N } ∈ R N × 3 \mathcal{P}=\left\{p_{i} \mid i=1, \cdots, N\right\} \in \mathbb{R}^{N \times 3} P={pi∣i=1,⋯,N}∈RN×3, N N N 表示点云的数量, ( x , y , z ) (x, y, z) (x,y,z)表示笛卡尔坐标系下的坐标。
简单介绍下PointNet++
简单介绍下RSCNN
简单介绍下Point Transformer
3.2 PointMLP的框架结构

整个结构用数学语言表示为:
g i = Φ pos ( A ( Φ pre ( f i , j ) , ∣ j = 1 , ⋯ , K ) ) g_{i}=\Phi_{\text {pos }}\left(\mathcal{A}\left(\Phi_{\text {pre }}\left(f_{i, j}\right), \mid j=1, \cdots, K\right)\right) gi=Φpos (A(Φpre (fi,j),∣j=1,⋯,K))
其中 Φ pre ( ⋅ ) \Phi_{\text {pre }}(\cdot) Φpre (⋅)和 Φ pos ( ⋅ ) \Phi_{\text {pos }}(\cdot) Φpos (⋅)是residual point MLP blocks:
- Φ pre ( ⋅ ) \Phi_{\text {pre }}(\cdot) Φpre (⋅)用于从局部区域学习共享权值
- Φ pos ( ⋅ ) \Phi_{\text {pos }}(\cdot) Φpos (⋅)用于提取深度聚合特征
具体而言,残差块里包含了许多一样的MLP组合(MLP ( x ) + x (x)+x (x)+x):MLP(FC)+normalization+ activation layers(重复两次)
A ( ⋅ ) \mathcal{A}(\cdot) A(⋅) 表示max-pooling
上式只表示一个阶段,可以重复 s s s次。
PointMLP有着如下优点:
- MLP结构使得处理点云时具有序列不变性。
- 残差的引入可以使得网络构造的更深。
- 没有复杂的特征提取器,主要的就是feed-forward MLP
在没有提前声明的情况下, s = 4 s=4 s=4,2个 Φ pre ( ⋅ ) \Phi_{\text {pre }}(\cdot) Φpre (⋅),2个 Φ pos ( ⋅ ) \Phi_{\text {pos }}(\cdot) Φpos (⋅)。选择k-nearest neighbors算法提取邻居, K = 24 K=24 K=24。
3.3 Geometric Affine Module
由于点云的局部区域就具有稀疏和不规则性,只使用间的MLP网络的性能并不好。不同局部区域的多个几何结构可能需要不同的提取设备,但共享的残留MLP难以实现这一点。
令 { f i , j } j = 1 , ⋯ , k ∈ \left\{f_{i, j}\right\}_{j=1, \cdots, k} \in {fi,j}j=1,⋯,k∈ R k × d \mathbb{R}^{k \times d} Rk×d表示 f i ∈ R d f_{i} \in \mathbb{R}^{d} fi∈Rd 的邻居,有 k k k个点,每个邻居点 f i , j f_{i, j} fi,j 是一个 d d d维向量。将局部相邻的点变换为:
{ f i , j } = α ⊙ { f i , j } − f i σ + ϵ + β , σ = 1 k × n × d ∑ i = 1 n ∑ j = 1 k ( f i , j − f i ) 2 , \left\{f_{i, j}\right\}=\alpha \odot \frac{\left\{f_{i, j}\right\}-f_{i}}{\sigma+\epsilon}+\beta, \quad \sigma=\sqrt{\frac{1}{k \times n \times d} \sum_{i=1}^{n} \sum_{j=1}^{k}\left(f_{i, j}-f_{i}\right)^{2}}, {fi,j}=α⊙σ+ϵ{fi,j}−fi+β,σ=k×n×d1i=1∑nj=1∑k(fi,j−fi)2,
其中 α ∈ R d \alpha \in \mathbb{R}^{d} α∈Rd, β ∈ R d \beta \in \mathbb{R}^{d} β∈Rd是可学习的参数, ⊙ \odot ⊙表示两个矩阵元素间相乘, ϵ = \epsilon= ϵ= 1 e − 5 1 e^{-5} 1e−5是一个为了数值稳定性的数。 σ \sigma σ 是系数,描述了所有局部和通道的特征差异,并保留了原始的几何特征。
3.4 计算复杂度和Elite版
全连接层参数很多,复杂度也很高,提出了bottleneck结构。我们选择将中间FC层的通道数减少 r r r倍,并增加通道数作为原始特征映射。
在PointMLP-elite中, r = 4 r=4 r=4
4.实验
4.1 Shape classification on ModelNet
ModelNet40:40个类别,9843个训练模型,2468个测试模型。
Metric:class-average accuracy (mAcc)和overall accuracy (OA)
训练了300个epochs
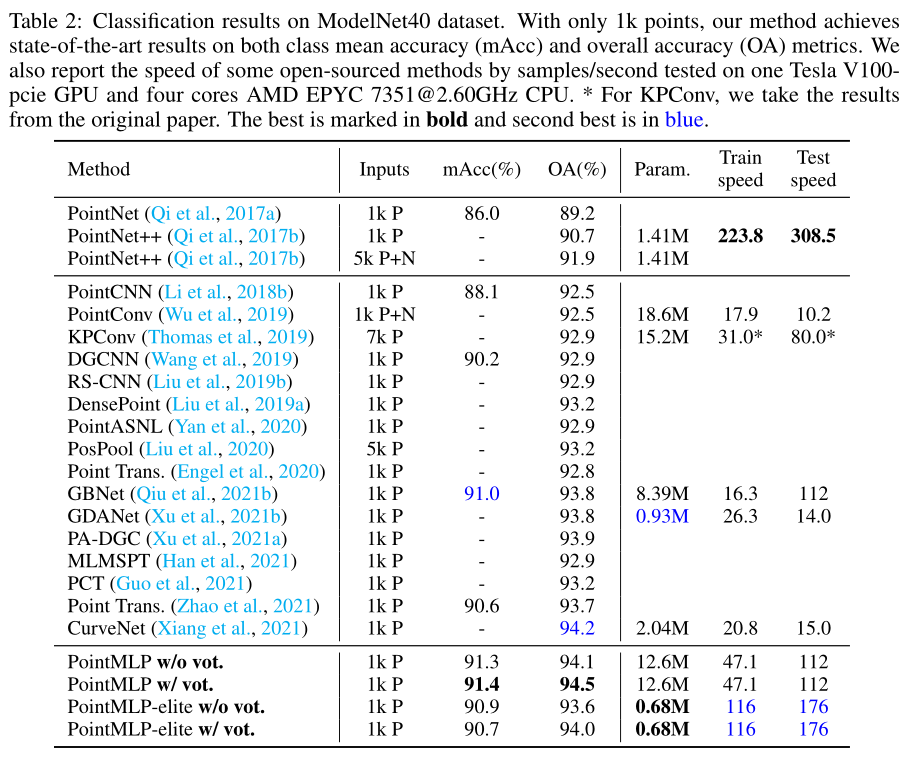
模型的复杂度不能直接反应效能。
4.2 Shape classification on ScanObjectNN
ScanObjectNN:真实世界中的重建模型,它包含15000个对象,这些对象分为15个类,在现实世界中有2902个唯一的对象实例。数据集中存在噪声、遮挡,选择最难的PB_T50_RS。
e p o c h s = 200 , b a t c h = 32 epochs=200, batch=32 epochs=200,batch=32,训练了四次,并将标准差记录在下表中。
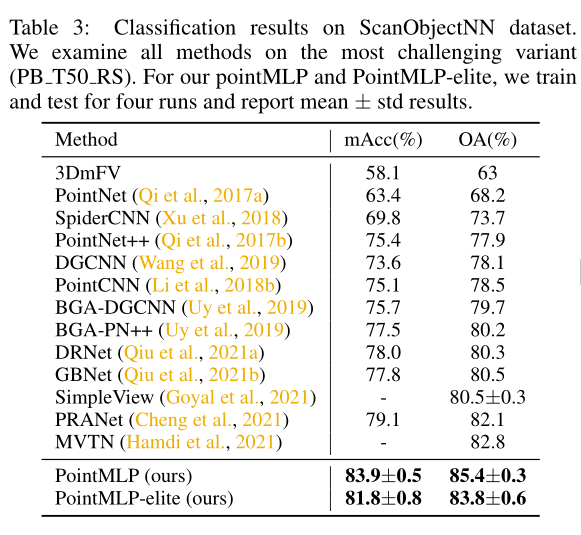
类别整体精度和平均精度很相近,证明方法很鲁棒。
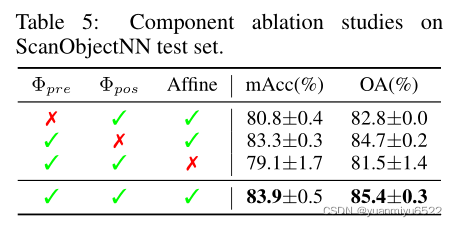
4.3 消融实验
网络深度
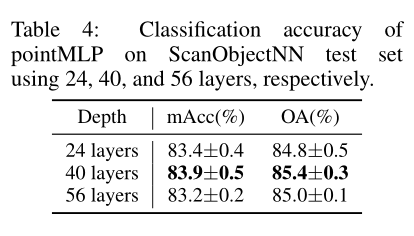
- 层数越多,效果不一定越好,但是标准差会变小
- 无论哪种深度,效果都比现在最优的效果好
Geometric Affine Module
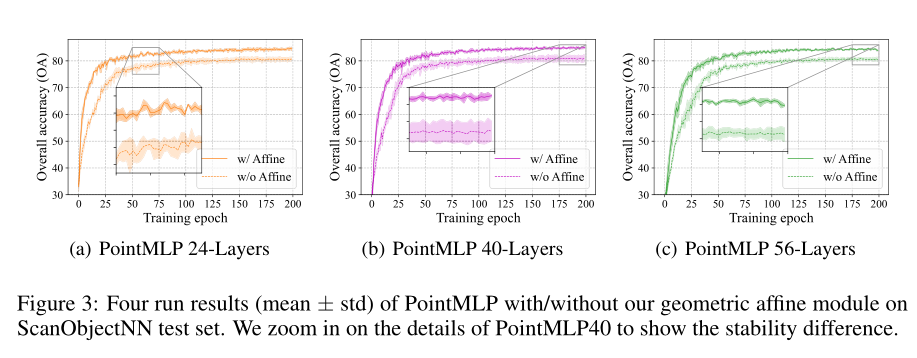
- the geometric affine module将局部输入特征映射为normal分布,更容易训练
- the geometric affine module通过局部质心和方差的通道距离对局部几何信息进行隐式编码,弥补了几何信息的不足。
- 结果更鲁棒。
成份消融实验
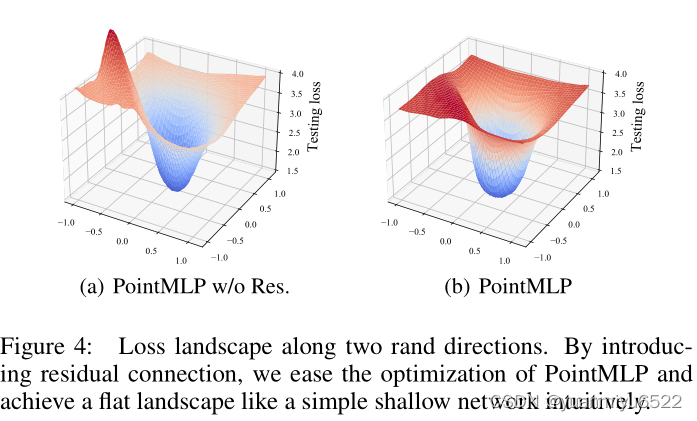
Loss landscape
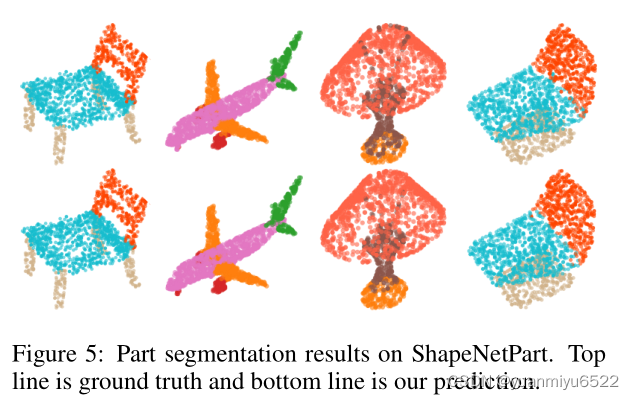
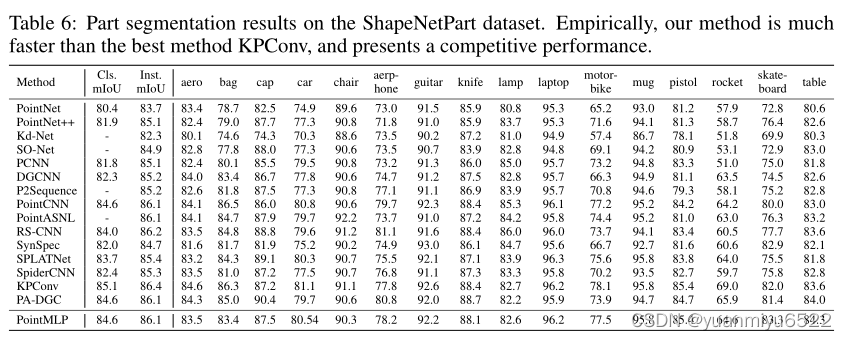
4.4 Part segmentation
ShapeNetPart:16个类别,16,881个形状,每个物体的部分为2-6个。
5.结论
- residual MLPs
- geometric affine module
- PointMLP-elite
6. 附录
6.1 PointMLP detail

PointMLP 和 PointMLP-elite有着以下的区别:
- 减少了residual point MLP blocks的数量
- Embedding的维度从64减少到32
- 通过引入bottleneck结构,参数减少了4倍
6.2 Experiment setting detail
ModelNet40
PyTorch + Tesla V100 GPU
epochs =300
batchsize = 32
synchronous SGD
Nesterov momentum = 0.9
weight decay = 0.0002
initial learning rate = 0.1
input point = 1024
ScanObjectNN
epochs =200
其他参数同上
ShapeNetPart
input point = 2048
range = [0.67, 1.5]
其他参数同PointNet一样
6.3 More detialed ablation studies
Skip connection
试着在PointNet++上加了两个skip connection,在ModelNet40上的分类精度变为92.7%。
Pre-MLP block vs. Pos-MLP block
去掉Pos-MLP block的话效果会变得不好,表明
- Pos-MLP block还是很重要的
- 增加Pre-MLP block的数量没有必要
Geometric Affine Module Applications
将Geometric Affine Module用到PointNet++上,在ModelNet40上的分类精度提高到了93.3%。
将Geometric Affine Module用到DGCNN上的效果反而变差了。
6.4 PointMLP depth
网络深度计算公式:
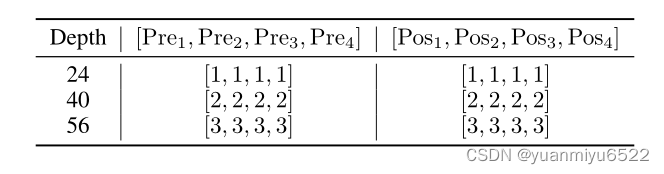
L = 1 + ∑ i = 1 4 ( 1 + 2 × Pre i + 2 × Pos i ) + 3 L=1+\sum_{i=1}^{4}\left(1+2 \times \operatorname{Pre}_{i}+2 \times \operatorname{Pos}_{i}\right)+3 L=1+i=1∑4(1+2×Prei+2×Posi)+3
Pre i \operatorname{Pre}_{i} Prei表示 Φ pre \Phi_{\text {pre }} Φpre 的重复数量, Pos i \operatorname{Pos}_{i} Posi表示 Φ pos \Phi_{\text {pos }} Φpos 的重复数量,不算Batch Normalization和activation functions,每个块里有两个MLP层,最终的网络深度配置如下图所示。
论文写作亮点
- unfavorable latency 不利的因素
- Lately 最近
- endow 赋予… v.
- gratifying 令人满足的 adj.
- saturate 简单的、紧凑的 adj.
- eschew 避免 v.
- regime 体系 n.
- seamlessly 无限接近地 adv.
- flesh out 使…丰满,充实 v.
- Unless explicitly stated
- outbeat 胜过 v.
这篇关于【点云处理之论文狂读前沿版1】——Rethinking Network Design and Local Geometry in Point Cloud: A Simple Residual MLP的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






