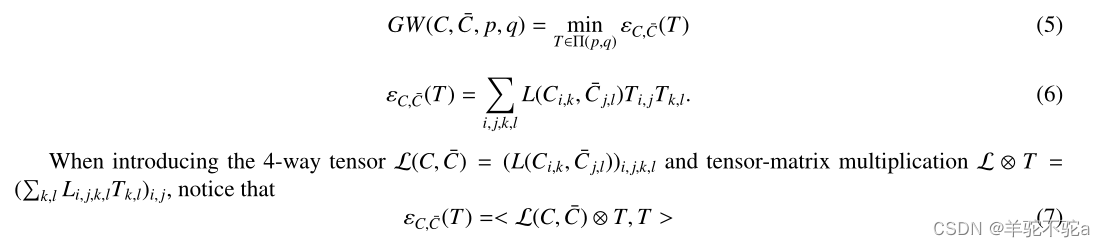【最优传输论文十九】2020 AAAI - Gromov-wasserstein factorization models for graph clustering

本文主要是介绍【最优传输论文十九】2020 AAAI - Gromov-wasserstein factorization models for graph clustering，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

1. motivation

作为机器学习的一种重要方法，因式分解模型明确地探索了高维观测的内在结构，已被广泛应用于数据聚类、降维、推荐系统等学习任务。特别是，因式分解模型将高维观测分解成特定标准下的一组原子，并相应地获得它们的潜在表示。对于每个观测值，其潜在表示对应于与原子相关的系数。

然而，大多数现有的分解模型，如主成分分析(PCA)、非负矩阵分解(NMF) 和字典学习，都是为具有相同维度的矢量化样本而设计的。它们不适用于结构数据，例如图和点云。在图聚类任务中，观察到的图通常具有不同数量的节点，并且它们的节点之间的对应关系通常是未知的，即图是未对齐的。这些未对齐的图不能直接表示为向量。尽管近年来在图神经网络的帮助下提出了许多图嵌入方法，它们通常需要节点属性和标签等附加信息，这些信息在实践中可能不可用。此外，由于没有明确的因式分解机制，这些方法无法找到可以重构观察到的图的原子，因此，由它们导出的图嵌入不如由因式分解模型导出的潜在表示具有可解释性。因此，迫切需要建立一种适用于结构数据的灵活的因子分解模型。

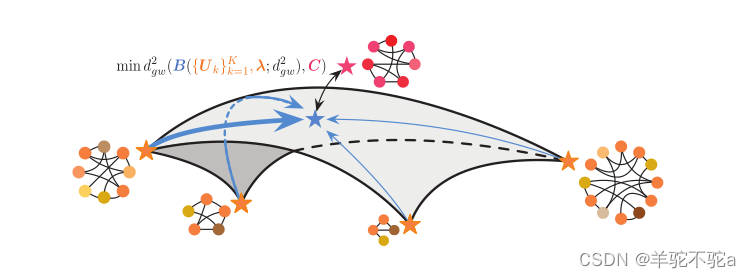
为了克服上述挑战，本文提出了一种基于Gromov-Wasserstein (GW)差异的Gromov-Wasserstein因式分解(GWF)模型。如图1所示，对于每个观测到的图(即红色恒星)，GWF模型基于一组原子(即对应于四个图的橙色恒星)重建它。重建(即蓝星)是原子的GW质心，使其与观测图的差异最小化。原子的重量(即具有不同宽度的蓝色箭头)表示观察到的图的嵌入。学习GW质心可以重建原子图，而GW差异提供了一个伪度量来测量它们的重建误差。本文设计了一个有效的近似算法来学习原子和图嵌入(原子的权重)，展开GW差异和质心的循环计算，并基于包络定理简化反向传播。近似算法可以基于近点算法(PPA) 或Bregman乘法器交替方向法(BADMM) 来实现。

GWF模型显式地将图分解为一组原子。原子为所有的观测所共有，而它们的重量则因人而异。这种模式有几个优点。首先，它具有很高的灵活性。观察到的图、原子和GW质心可以有不同的大小，它们的排列是通过它们之间的GW差所对应的最优输运来实现的。其次，该模型与现有模型兼容，可以基于反向传播学习，可以作为有监督学习中的结构正则器。在数据方面，无论图是否带有节点属性，该模型都是适用的。第三，GWF模型得到的图嵌入更易于解释——它们直接反映了原子的重要性。本文首次尝试建立了图的显式分解机制，扩展了传统的GW差异下的分解模型。实验结果表明，GWF模型在图聚类任务中取得了令人鼓舞的效果。

图1:Gromov-Wasserstein分解模型的说明。每个星形表示一个图形。对于每个图，黑色曲线表示它的边缘，不同颜色的点是它的节点，具有不同的属性。

2. Model

将一个图表示为它的邻接矩阵 $C\in \mathbb{R}^{N\times N}$ ，它的元素是非负的。当图具有d维节点属性时，将其节点属性表示为矩阵 $F\in \mathbb{R}^{N\times D}$ 。进一步，对于图，将其节点的经验分布表示为 $\mu \in\Delta ^{N-1}$ ，其中 $\Delta ^{N-1}=\left \{ x=\left [ x_{n} \right ]\in\mathbb{R}^{N}|x_{n}\geq 0,and \sum_{k}x_{k}=1 \right \}$ 表示一个(N−1)-单纯形。假设经验分布是均匀的,也就是说, $\mu =\frac{1}{N}1_{N}$ 。给一组观测值 $\left \{ C_{i}\in [0,\propto )^{N_{i}\times N_{i}},\mu _{i}\in \Delta ^{N_{i}-1} \right \}_{i=1}^{I}$ ,我们的目标是设计一个K原子分解模型 $U_{1:K}=\left \{ U_{k}=\left [ u_{ij}^{k}\in [0,\propto )^{N_{k}\times N_{k}} \right ] \right \}_{k=1}^{K}$ ,代表每个观察Ci作为嵌入向量 $\lambda _{i}=\left [ \lambda _{ik} \right ]\in \mathbb{R}^{K}$ ,这样的元素 $\lambda _{ik}$ 可以解释为第K个原子的第i个观察值的意义。假设每个λi也在一个(K−1)-单纯形中，即当i = 1,...,I时， $\lambda _{i} \in\Delta ^{K-1}$ ，通常对于不同的 $C_{i}$ 和 $C_{j}$ ，它们的节点是不对齐的， $N_{i}\neq N_{j}$ 。

2.1 Revisiting factorization models

许多现有的因式分解模型假设每个向量化数据 $y\in \mathbb{R}^{N}$ 可以表示为K个原子的加权和，即 $y=\sum _{k}\lambda _{k}a_{k}=A\lambda$ ，其中 $A=\left [ a_{k}\in \mathbb{R}^{N\times N} \right ]$ 包含k个原子， $\lambda =\lambda _{k}\in \mathbb{R}^{K}$ 是y的潜在表示。给定一组观测值 $\left \{ y_{i} \right \}_{i=1}^{I}$ ，学习分解模型的一个简单方法是解决以下优化问题:

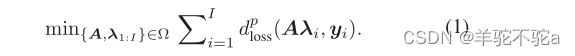
其中，Ω表示对A和 $\lambda _{1:I}$ 的约束。dloss(·，·)定义了yi与其估计值Aλi之间的距离，作为损失函数，p表示dloss的阶数。这个优化问题可以专门化为许多经典模型:在没有任何约束的情况下，PCA 将dloss设置为欧氏距离，p = 2;稳健PCA 将dloss设为L1范数，p = 1;NMF将Ω集合为非负矩阵集合;Wasserstein字典学习将dloss设置为Wasserstein距离，Ω设置为具有规范化列的非负矩阵的集合。

更进一步，当 $\lambda \in\Delta ^{K-1}$ 时，线性分解模型λ对应于学习欧几里德空间中原子的质心，可以重写为

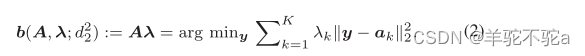
其中，y表示优化问题的变量，其最优解为λ(即yi在(1)中的估计)。将欧几里德度量推广到其他度量，得到了非线性因子分解模型，即 $b(A,\lambda ;d_{b}^{q}):=min_{y}\sum_{k=1}^{K}\lambda _{k}d_{b}^{q}(y,a_{k})$ ，其中db(·，·)是用来计算质心的度量，q是阶数。例如，当k = 1,...,K时， $a_{k} \in\Delta ^{N-1}$ , db为Wasserstein度量， $b(A,\lambda ;d_{b}^{q})$ 对应于Wasserstein分解模型。综上所述，许多现有的因式分解模型处于以下框架:

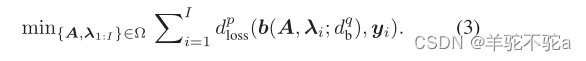
2.2 Gromov-Wasserstein分解

如前所述，当观测数据为图时，即将向量 $y _{1:I}$ 和(3)中的原子A分别替换为图 $C _{1:I}$ 和它们的原子 $U _{1:K}$ 时，经典的度量就不适用了。在这种情况下，将(3)中的dloss和db设为GW差值，记为dgw，得到提出的GWF模型。GW差异是Gromov-Wasserstein距离在度量空间上的延伸:

定义(Gromov-Wasserstein距离)设 $(X,d_{X},u_{X})$ 和 $(Y,d_{Y},u_{Y})$ 是两个度量度量空间，其中(X, dX)是紧度量空间，uX是X上的Borel概率测度((Y, dY, uY)以相同的方式定义)。对于p∈[1，∞]，定义p阶Gromov-Wasserstein距离 $d_{gw}(u_{X},u_{Y})$ 为

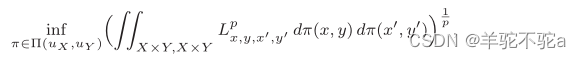
$L_{x,y,x',y'}=\left | d_{X}(x,x')-d_{Y}(y,y') \right |$ 是损失函数，Π(uX, uY)是X× Y上以uX和uY为边际的所有概率测度的集合。由于Gromov-Wasserstein的条件很严格，不适合广泛的机器学习任务，所以peyr等人将Gromov-Wasserstein距离放宽为Gromov-Wasserstein差异。它包括用不相似度量代替dx和dY，即它们不一定是正的，满足三角不等式，并更灵活地定义L，如均方误差(MSE)或kl散度。

因此，它在结构数据(如图表)上定义了一个灵活的伪度量和点云。特别地，给定两个图 $\left \{ C_{s}=\left [ c_{ij}^{s} \right ]\in \mathbb{R}^{N_{s}\times N_{s}},C_{t}=\left [ c_{i'j'}^{t} \right ]\in \mathbb{R}^{N_{t}\times N_{t}} \right \}$ 和它们的经验实体分布 $\left \{ \mu _{s}\in \mathbb{R}^{N_{s}},\mu _{t}\in \mathbb{R}^{N_{t}} \right \}$ ，它们之间的二阶gw差异，记为 $d_{gw}(C_{s},C_{t})$ ，定义为

$\Pi (\mu _{s},\mu _{t})=\left \{ T\geq 0|T1_{N_{t}}=\mu _{s}, T^{T}1_{N_{s}}=\mu _{t}\right \}$ 。

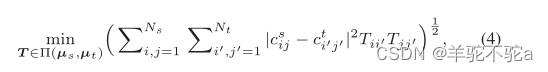
最优T表示Cs节点与Ct节点之间的最优传输。将(4)重写为

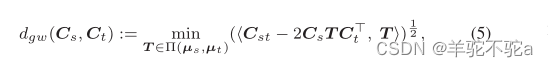
<.,.>表示矩阵的内积， $C_{st}=\left ( C_{s}\odot C_{s} \right )\mu _{s}1_{N_{t}}^{T}+1_{N_{s}}\mu _{t}^{T}\left ( C_{t}\odot C_{t} \right )^{T}$ ， $\odot$ 表示矩阵的哈达玛积。GW差异的计算对应于一个最优运输问题。这个问题可以通过基于熵正则化的方法或近点算法迭代地解决。

给定K个图 $\left \{ U_{k} \right \}_{k=1}^{K}$ ，它们的权值 $\lambda =\left [ \lambda _{k} \right ]\in \bigtriangleup ^{K-1}$ ，根据式(5)中的GW差异，可以很自然地定义它们的二阶质心:

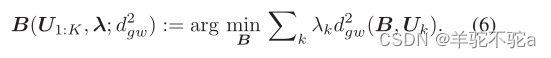
根据定义，我们可以发现GW质心的计算涉及迭代求解K个最优输运问题。

将 $d_{gw}$ 代入式(3)，设p = q = 2，可得到提出的Gromov-Wasserstein分解模型:

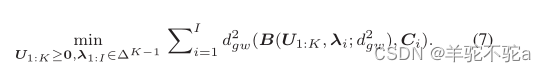
在该模型中，每个图Ci由原子的GW质心U1:K来估计。与原子相关的权重构成嵌入向量λi。原子和嵌入都学会了最小化观察图与基于GW重心的估计之间的GW差异。如上所述，要求每个原子的元素是非负的，并使每个嵌入在(K−1)-单纯形中。

如图1所示，这个GWF模型应用几个原子来构造一组图，其中每个图是原子的重心。每个观测图由集合中最相似的图重构，重构图对应的嵌入向量λi表示不同原子的显著性。

观察到的图的嵌入可以用作许多下游任务的特征，例如图聚类。GWF模型非常灵活——原子和观察到的图可以有不同的大小。所提出的GWF模型在学习阶段不依赖于任何附带信息，如图的标签。此外，由于使用了显式因子分解机制，该模型比许多现有方法具有更好的可解释性。

3. Learning Algorithm

3.1 Reformulation of the problem

学习GWF模型具有挑战性，因为(7)是一个高度非线性的约束优化问题。由式(5,6)可知，GW差异和GW质心的计算分别对应两个优化问题，因此式(7)中的GWF模型是多个不同变量优化任务的复杂组合。面对这样一个难题，重新表述了它，简化了它的计算。

目标变量的再参数化。为了将(7)重新表述为无约束问题，我们进一步将参数U1:K和λ1:I再次进行参数化

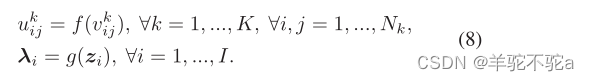
其中 $V_{1:K}=\left \{ V_{k}=\left [ v_{ij}^{k}\in \mathbb{R}^{N_{k}\times N_{k}} \right ] \right \}_{k=1}^{K}$ 和 $z_{1:I}=\left \{ z_{i}=\left [ z_{ik} \right ]\in \mathbb{R}^{K}\right \}$ 是新的无约束参数，f(·)= ReLU(·)和g(·)= Softmax(·)是将新参数映射到原问题可行域的两个函数。使用ReLU(·)来追踪边缘稀疏的原子。因此，使用zi作为图Ci的嵌入。

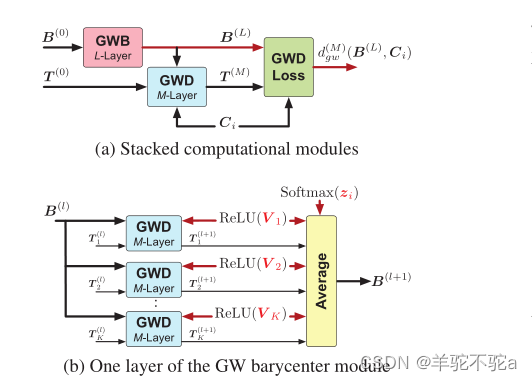
展开循环。对于每个Ci，其(7)中目标函数的前馈计算对应两个步骤:i)迭代求解K个最优输运问题，以估计一个GW质心;ii)再求解一个最优输运问题，得出GW质心与Ci之间的GW差异。每一步都包含最优传输矩阵的循环计算。我们将环路展开为堆叠模块，如图2(a)所示。具体来说，我们设计了一个M层的Gromov-Wasserstein差异(GWD)模块来实现GW差异的近似。在此基础上，进一步提出了一种具有L层的GW质心(GWB)模块，以获得GW质心的近似。图2(b)展示了GWB模块的一层。

在此基础上，将式(7)重新表述为

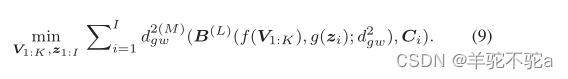
图2:(a)用于学习GWF模型的堆叠模块。(b) GWB模块一层。图中红色箭头表示前馈计算和反向传播的路径，黑色箭头表示前馈计算的路径。GWD对应算法1和算法2,GWB对应算法3,GWD损失对应(12)。

3.2 Implementations of the modules

GWD模块是算法的主干。在本文中提出了两种实现该模块的方案。

第一个是近点算法（PPA）。给定{Cs， μs}和{Ct， μt}， PPA迭代求解(5)。在每次迭代中，它解决了以下问题:

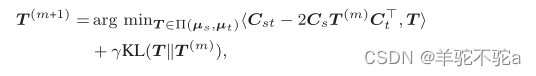
其中KL(T ||T (m))计算最优传输矩阵与其先前估计之间的KL散度。通过一步Sinkhorn Knopp更新近似地解决了这个问题。经过M次迭代，得到了最优传输矩阵的M步逼近。因此，给出了算法1中基于ppa的GWD模块的方案。该方法基于(Xu et al . 2019)中的工作，将(peyr， Cuturi, and Solomon 2016)中的熵正则化器替换为KL散度。 PPA在稳定性和收敛性方面都优于熵GW方法。

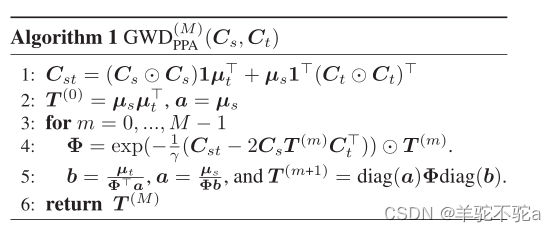
除了基于ppa的GWD模块外，我们还提出了一种基于Bregman乘法器交替方向法(BADMM)的GWD模块。具体地说，引入一个辅助变量S，将(5)重写为

在 $\Pi (\mu _{s},\cdot )=\left \{ T\geq 0|T1_{M}=\mu _{s} \right \}$ 和 $\Pi (\cdot ,\mu _{t})=\left \{ T\geq 0|T^{T}1_{N}=\mu _{t} \right \}$ 。我们进一步引入对偶变量Z，并通过以下三步求解问题（10）。

算法2给出了基于badmm的GWD模块的方案。

BADMM算法最初是为计算Wasserstein距离而设计的。据我们所知，本文是第一次尝试应用BADMM来计算GW差异。

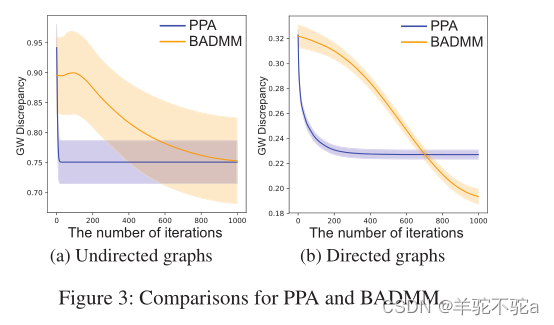
我们在合成图上测试了这两个GWD模块，发现它们适用于不同的场景。特别地，我们分别合成了100对无向图和100对有向图。每个图有100个节点。有向图是基于BarabásiAlbert (BA)模型生成的。对于每个有向图，我们将它的邻接矩阵加到它的转置上，从而得到一个无向图。对于每一对图，使用GWD模块计算两图之间的GW差异，然后计算每一步GW差异的平均值和标准差。基于ppa的模块和基于badmm的模块的比较如图3(a)和3(b)所示。对于无向图和有向图，基于ppa的模块比基于badmm的模块收敛到稳定的最优传输矩阵所需的步骤更少。然而，基于badmm的模块在应用于有向图时可以实现较小的GW差异。换句话说，我们需要根据观察图的结构和计算复杂度的实际约束来选择不同的GWD模块。

GWB模块是在GWD模块的基础上实现的。如算法3所示，给定初始GW质心B(0)及其经验分布μb，得到了GW质心的l阶近似和质心与原子之间的最优输运矩阵。通过交替优化来计算GW质心:1)更新原子与质心之间的最优输运;2)相应地更新重心。图2b显示了GWB模块的一个步骤(即算法3中的2-4行)，其中T (l) k是GWB模块第l步估计的最优运输。通过调用具有M个内部迭代的gwd模块来更新它，并且输出表示为T (l+1) k。

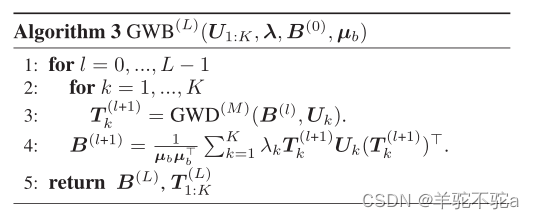
3.3 基于包络定理的反向传播

给定上述模块，可以计算 $d_{gw}^{2(M)}(B^{(L)}(f(V_{1:K})),g(z_{i});d_{gw}^{2},C_{i})$ ，并应用反向传播来更新变量V1:K和z1:L。在这里，利用包络定理来简化反向传播的计算。根据当前参数计算了每个最优传输矩阵，即用于计算GW质心的 $T_{1:K}^{(L)}$ 以及GW质心与观测图之间的 $T^{(M)}$ 。因此，目标函数为

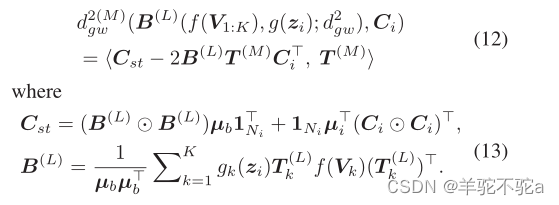
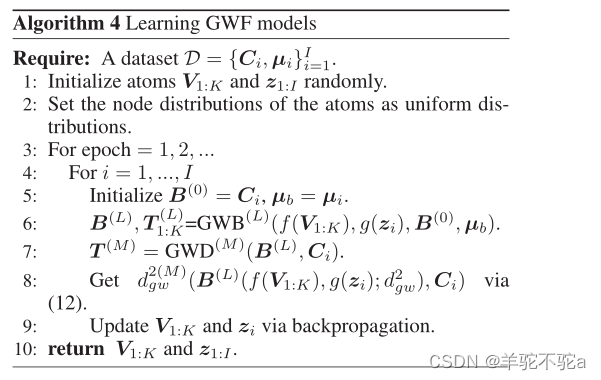
基于上述包络定理，计算了具有固定最优传输矩阵的(12)的梯度。在应用反向传播时，可以忽略最优传输矩阵的梯度，从而大大提高了算法的效率。综上所述，通过算法4学习GWF模型。

3.4 Extensions

给定更多的附加信息，我们可以将GWF模型扩展到更复杂的场景。

用标签学习。一些图被标记时，可以通过添加标签相关损失来实现GWF模型的半监督学习:

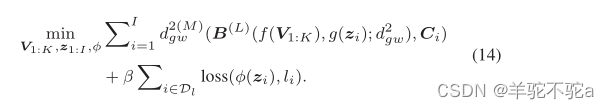
其中loss(φ(zi)， li)表示与标签相关的损失，其中li是第i个图的标签，φ(·)是将嵌入zi映射到标签空间的可学习函数。损耗的典型选择是交叉熵(MLP(zi))， li)。

使用节点属性学习。 每个图的节点经常都与向量化特征相关联。在这种情况下，观测值为{Ci， μi, Fi}Ii=1，其中Fi∈RNi×D表示节点的特征。据此，GWF模型的原子变为{U1:K, H1:K}，其中Uk∈[0，∞)Nk×Nk为第K个原子的邻接矩阵，Hk∈RNk×D为其节点的特征。

为了学习这个GWF模型，可以用(V ayer et al . 2019a)中融合的Gromov-Wasserstein (FGW)差异来代替GW差异:对于两个图{Cs， μs, Fs}和{Ct， μt, Ft}，它们的FGW差异为

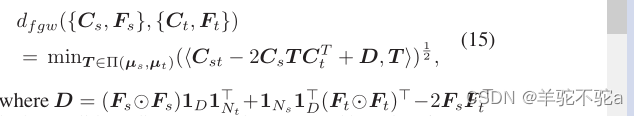
D为基于特征计算的欧氏距离矩阵。可以通过GWD模块近似FGW差异-只需将算法1(或算法2)中的第一行替换为 $C_{st}=\left ( C_{s}\odot C_{s} \right )1\mu _{t}^{T}+\mu _{s}1^{T}\left ( C_{t}\odot C_{t} \right )^{T}+D$ 与(12)相似，损失函数变为

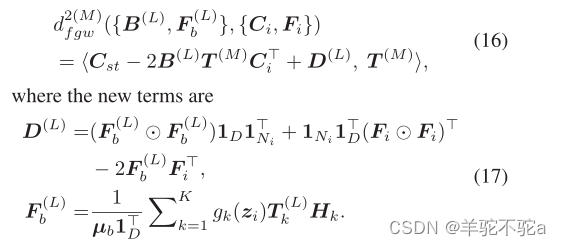
4. Related Work

4.1 GW discrepancy and its applications

伪度量结构的数据图表,GW差异已经应用于很多问题,例如,注册的3D点云,调整蛋白质网络的不同种类和匹配不同语言的词汇集合。对于具有节点属性的图，(V ayer et al . 2019a)的工作提出了FGW差异，将图结构之间的GW差异与节点属性之间的Wasserstein差异结合起来。在(peyr， Cuturi, and Solomon 2016)中提出了GW重心，实现了多图的插值。近年来，人们将GW差异作为学习机器学习模型的目标函数。(Bunne et al . 2019)中的工作通过最小化其样本之间的GW差异，在不可比拟的空间中训练耦合生成模型。(Xu et al . 2019)中的工作基于GW差异学习未对齐成对图的节点嵌入。现有的大部分工作都是通过Sinkhorn迭代计算GW差异，对于有N个节点的图，每次迭代的复杂度为O(N 3)。较高的计算复杂度限制了GW差异的应用。近年来，人们提出了许多GW差异的变体，例如递归GW差异和切片GW差异。尽管这些工作在许多任务中取得了令人鼓舞的结果，但它们都没有像我们一样考虑构建GromovWasserstein分解模型。

4.2 Graph clustering methods

图聚类对于许多实际应用都很重要，例如分子建模和社交网络分析。图划分是在一个图中寻找节点簇，而图聚类的目的是为不同的图寻找簇。这个问题的关键是嵌入未对齐的图。已经提出了许多方法来解决这个问题，其中大多数可以归类为基于核的方法，例如Weisfeiler-Lehman核。原则上，这些方法根据图的拓扑结构迭代地聚合节点特征。最近，这种策略在图卷积网络(GCNs)的帮助下变得可学习。已经提出了许多基于gcn的嵌入图的方法，例如大规模嵌入方法和分层嵌入方法。然而，这些方法依赖于节点的标签和属性，通常不适用于无监督学习。此外，由于它们的深度和高度非线性过程，它们所获得的嵌入往往具有较低的可解释性。除上述方法外，另一种策略——根据图的两两(融合)GW差异学习图的距离矩阵，并相应地应用谱聚类。该策略在无法获得节点侧信息的情况下也是可行的，但其计算复杂度很高。与上述方法相比，GWF模型提供了另一种策略，以可扩展和理论支持的方式嵌入图，并使嵌入在分解模型框架中可解释。

这篇关于【最优传输论文十九】2020 AAAI - Gromov-wasserstein factorization models for graph clustering的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！