Transformer中的Self-Attention和Multi-Head Attention

本文主要是介绍Transformer中的Self-Attention和Multi-Head Attention，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

2017 Google 在Computation and Language发表

当时主要针对于自然语言处理（之前的RNN模型记忆长度有限且无法并行化，只有计算完ti时刻后的数据才能计算ti+1时刻的数据，但Transformer都可以做到）

文章提出Self-Attention概念，在此基础上提出Multi-Head Atterntion

下面借鉴霹雳吧啦博主的视频进行学习：

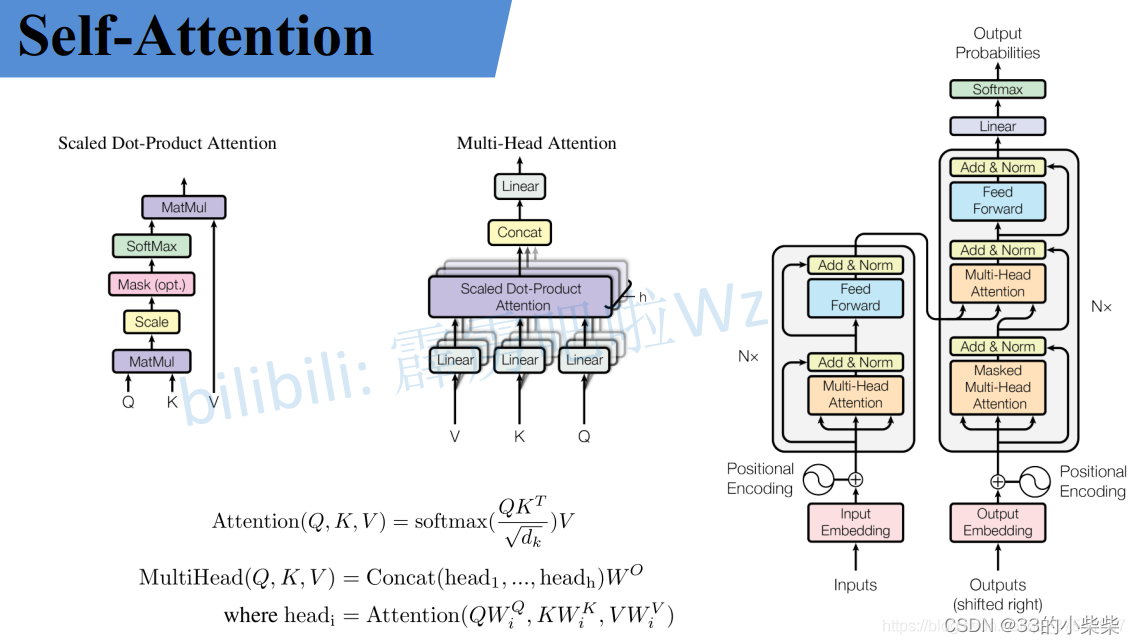
Self-Attention

假设输入的序列长度为2，输入就两个节点x1，x2，然后通过Input Embedding也就是图中的f(x)将输入映射到a1,a2。紧接着分别将a1，a2分别通过三个变换矩阵Wq，Wk，Wv（这三个参数是可训练的，是共享的）得到对应的 $q^{i},k^{i},v^{i}$ (直接使用全连接层实现)。

其中：

q代表query，后续会去和每一个k进行匹配

k代表key，后续会被每个q匹配

v代表从a中提取得到的信息

后续q和k匹配的过程可以理解成计算两者的相关性，相关性越大对应v的权重也越大。

假设 $a_{1}=(1,1),a_{2}=(1,0),W^{q}=\begin{pmatrix} 1,&1 \\ 0,&1 \end{pmatrix}$

那么 $q^{1}=(1,1)\begin{pmatrix} 1, &1 \\ 0, & 1 \end{pmatrix}=(1,2), q^{2}=(1,0)\begin{pmatrix} 1, &1 \\ 0, & 1 \end{pmatrix}=(1,1)$

因为Transformer是并行化的，可以直接写成：

$\begin{pmatrix} q^{1}\\ q^{2} \end{pmatrix}=\begin{pmatrix} 1, &1 \\ 1, &0 \end{pmatrix}\begin{pmatrix} 1, &1 \\ 0, &1 \end{pmatrix}=\begin{pmatrix} 1, &2 \\ 1, &1 \end{pmatrix}$

同理可以得到 $\begin{pmatrix} k^{1}\\ k^{2} \end{pmatrix}$ 和 $\begin{pmatrix} v^{1}\\ v^{2} \end{pmatrix}$ ，那么求得的 $\begin{pmatrix} q^{1}\\ q^{2} \end{pmatrix}$ 就是原论文中的Q， $\begin{pmatrix} k^{1}\\ k^{2} \end{pmatrix}$ 是K， $\begin{pmatrix} v^{1}\\ v^{2} \end{pmatrix}$ 是V。接着 $q^{1}$ 和每个k进行match，点乘操作，接着除以 $\sqrt{d}$ 得到对应的 $\alpha$ ，其中d代表向量 $k^{i}$ 的长度，除以 $\sqrt{d}$ 的原因是在论文中的解释“进行点乘后数值很大，导致通过softmax后梯度变得很小”，所以通过 $\sqrt{d}$ 进行缩放。

$\alpha _{1,1}=\frac{q^{1}\cdot k^{1}}{\sqrt{d}}=\frac{1*1+2*0}{\sqrt{2}}=0.71\\ \alpha _{1,2}=\frac{q^{1}\cdot k^{2}}{\sqrt{d}}=\frac{1*0+2*1}{\sqrt{2}}=1.41$

同理 $q^{2}$ 去匹配所有的k能得到 $\alpha _{2,i}$ ,统一写成乘法矩阵形式：

$\begin{pmatrix} \alpha _{1,1} & \alpha _{1,2} \\ \alpha _{2,1} & \alpha _{2,2} \end{pmatrix}=\frac{\begin{pmatrix} q^{1}\\ q^{2} \end{pmatrix}\begin{pmatrix} k^{1}\\ k^{2} \end{pmatrix}^{T}}{\sqrt{d}}$

接着对每一行即 $(\alpha _{1,1},\alpha _{1,2}),(\alpha _{2,1},\alpha _{2,2})$ 分别进行softmax处理得到 $(\widehat{\alpha} _{1,1},\widehat{\alpha} _{1,2}),(\widehat{\alpha} _{2,1},\widehat{\alpha} _{2,2})$ ,这里的 $\widehat{\alpha }$ 相当于计算得到针对每个v的权重。到这里完成了Attention(Q,K,V)公式中的 $softmax(\frac{QK^{T}}{\sqrt{d_{k}}})$ 部分。

上面已经计算得到 $\alpha$ ，即针对每个v的权重，接着进行加权得到最终结果

$b_{1}=\widehat{\alpha }_{1,1}\times v^{1}+\widehat{\alpha }_{1,2}\times v^{2}=(0.33,0.67)\\ b_{2}=\widehat{\alpha }_{2,1}\times v^{1}+\widehat{\alpha }_{2,2}\times v^{2}=(0.50,0.50)$

统一写成矩阵乘法形式：

$\begin{pmatrix} b_{1}\\ b_{2} \end{pmatrix}=\begin{pmatrix} \widehat{\alpha }_{1,1} & \widehat{\alpha }_{1,2}\\ \widehat{\alpha }_{2,1}& \widehat{\alpha }_{2,2} \end{pmatrix}\begin{pmatrix} v^{1}\\ v^{2} \end{pmatrix}$

Self-Attention的内容就结束了，总结下来就是论文中一个公式：

$Attention(Q,K,V)=softmax(\frac{QK^{T}}{\sqrt{d_{k}}})V$

Multi-Head Attention

多头注意力机制能联合来自不同head部分学习到的信息。

首先还是和Self-Attention模块一样将 $a_{i}$ 分别通过 $W^{q},W^{k},W^{v}$ 得到对应的 $q^{i},k^{i},v^{i}$ ,然后再根据使用的head的数目h进一步把得到的 $q^{i},k^{i},v^{i}$ 均分成h份。比如下图中假设的h=2然后 $q^{1}$ 拆分成 $q^{1,1},q^{1,2}$ ,那么 $q^{1,1}$ 就属于head1， $q^{1,2}$ 属于head2。

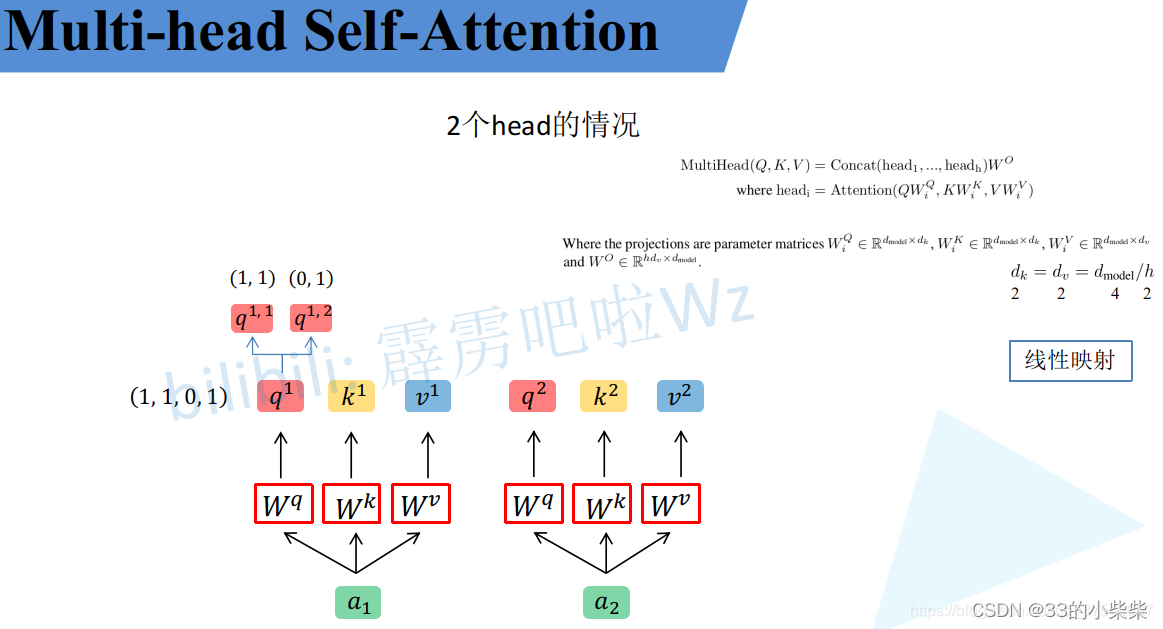
论文中写的通过 $W_{i}^{Q},W_{i}^{K},W_{i}^{V}$ 映射得到每个head的 $Q_{i},K_{i},V_{i}$ :

$head_{i}=Attention(QW_{i}^{Q},KW_{i}^{K},VW_{i}^{V})$

其实简单的均分也可以将 $W_{i}^{Q},W_{i}^{K},W_{i}^{V}$ 设置成对应值来实现均分，比如下图中的Q通过 $W_{1}^{Q}$ 就能得到均分后的 $Q_{1}$ 。

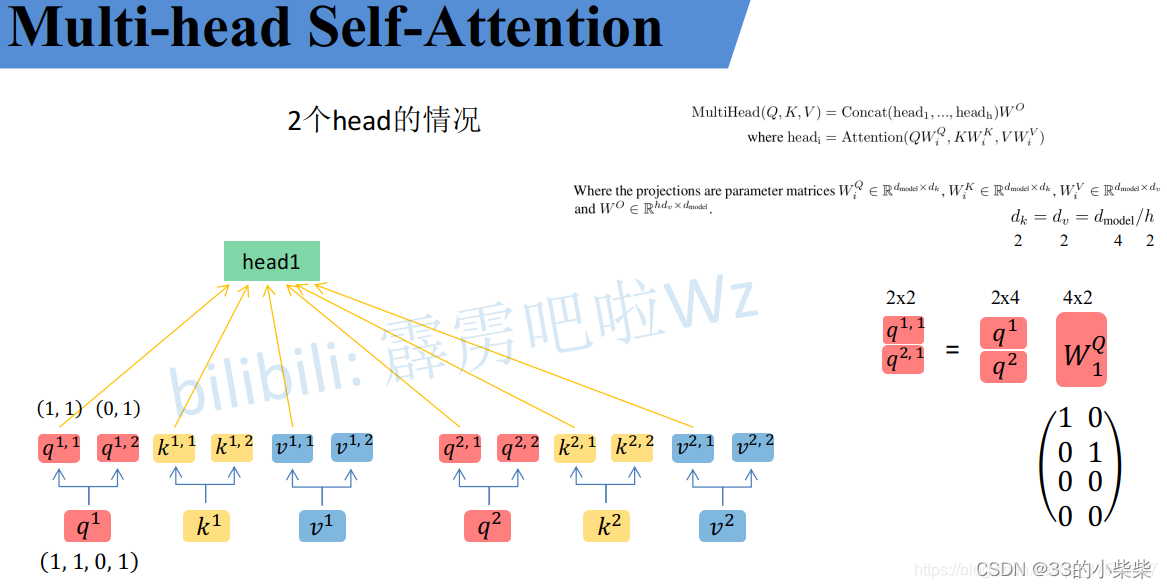
通过上述方法就能得到每个headi对应的 $Q_{i},K_{i},V_{i}$ 参数，接下来针对每个head使用Self-Atttention中相同的方法即可得到对应的结果。

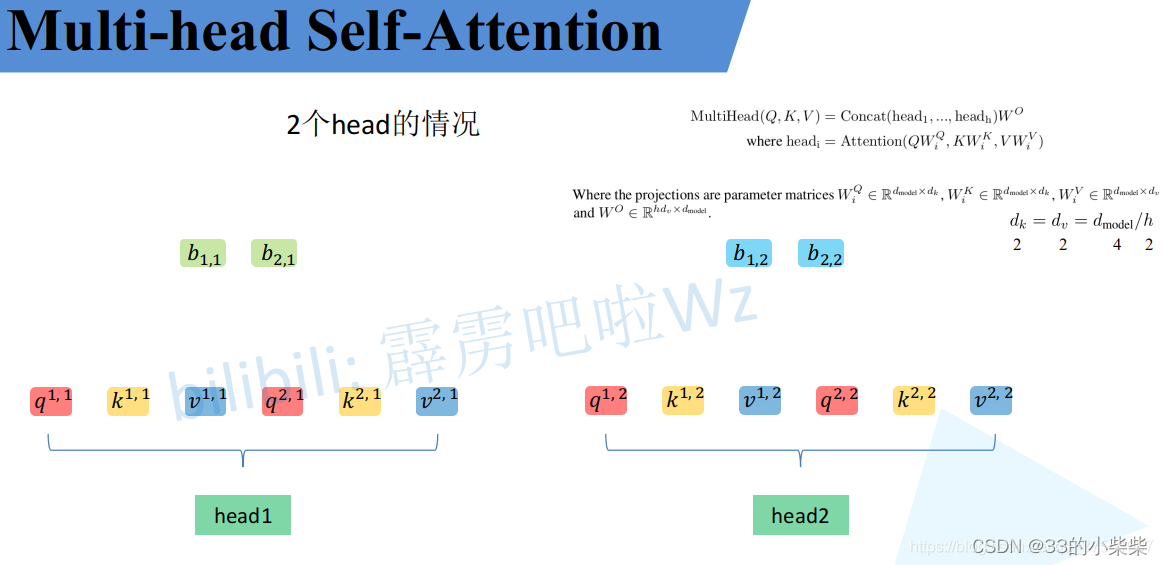
$Attention(Q_{i},K_{i},V_{i})=softmax(\frac{Q_{i}K_{i}^{T}}{\sqrt{d_{k}}})V_{i}$

接着将每个head得到的结果进行concat拼接，比如下图中b1,1(head1得到的b1)和b1,2(head2得到的b1)拼接在一起，b2,1(head得到的b2)和b2,2(head得到的b2)拼接在一起。

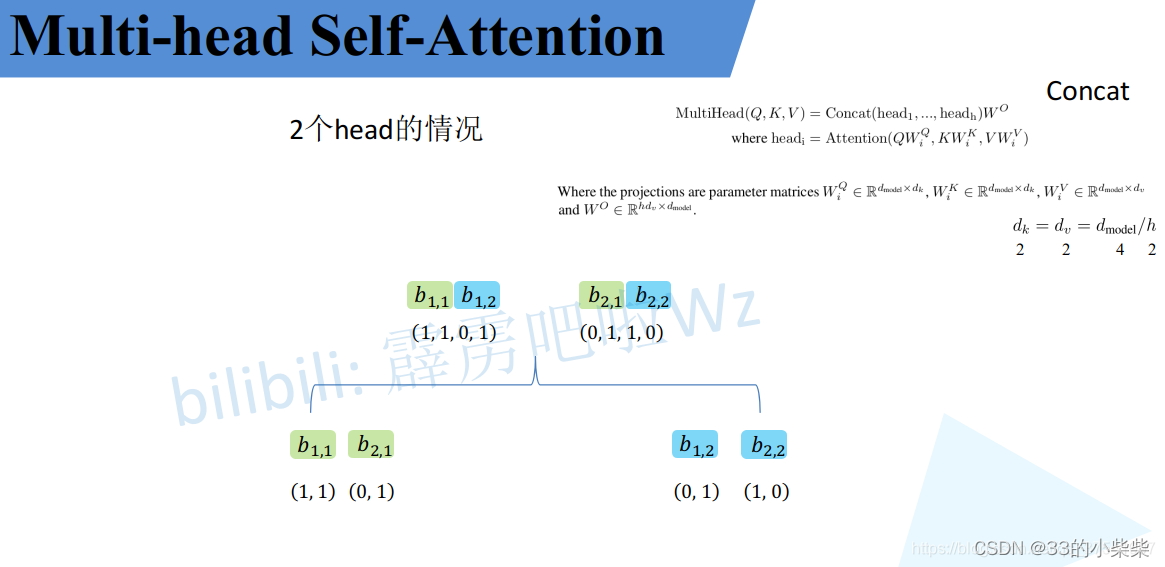
接着将拼接后的结果通过 $W^{O}$ (可学习的参数)进行融合，如下图，融合后得到最终的结果b1，b2

到这，总结下来就是论文中的两个公式：

$MultiHead(Q,K,V)=Concat(head_{1},...,heah_{h})W^{O}\\ where head_{i}=Attention(QW_{i}^{Q},KW_{i}^{K},VW_{i}^{V})$

import torch
from fvcore.nn import FlopCountAnalysisdef main():#Self-Attentiona1 = torch.nn.MultiheadAttention(embed_dim=512, num_heads=1)a1.proj = torch.nn.Identity() #removr Wo#Multi-Head Attentiona2 = torch.nn.MultiheadAttention(embed_dim=512, num_heads=8)#[batch_szie,num_tokens,total_embed_dim]t = torch.rand(32, 1024, 512)flops1 = FlopCountAnalysis(a1, t)print("Self-Attention FLOPs:", flops1.total())flops2 = FlopCountAnalysis(a2, t)print("Multi-Head Attention FLOPs:",flops2.total())if __name__ == '__main__':main()

Self-Attention FLOPs: 60129542144
Multi-Head Attention FLOPs: 68719476736

其实两者FLOPs的差异只是在最后的 $W^{O}$ 上，如果把Multi-Head Attentio的 $W^{O}$ 也删除(即把a2的proj也设置成Identity)，可以看出两者FLOPs是一样的：

Self-Attention FLOPs: 60129542144
Multi-Head Attention FLOPs: 60129542144

Positional Encoding

刚才计算是没有考虑到位置信息的。假设在Self-Attention模块中，输入a1,a2,a3得到b1,b2,b3。对于a1而言，a2和a3离它都是一样近且没有先后顺序。假设将输入的顺序改为a1,a2,a3，对结果b1是没有任何影响的。下面是Pytorch的实验，首先使用nn.MultiheadAttention创建一个Self-Attention模块（num_heads=1）,注意这里在正向传播过程中直接传入QKV，接着创建两个顺序不同的QKV变量t1和t2（主要是将q2,k2,v2和q3,k3,v3的顺序换了下），分别将这两个变量输入Self-Attention模块进行正向传播。

import torch
import torch.nn as nnm = nn.MultiheadAttention(embed_dim=2, num_heads=1)t1 = [[[1., 2.], #q1,k1,v1[2., 3.], #q2,k2,v2[3., 4.]]] #q3,k3,v3t2 = [[[1., 2.], #q1,k1,v1[3., 4.], #q3,k3,v3[2., 3.]]] #q2,k2,v2q, k, v  = torch.as_tensor(t1), torch.as_tensor(t1), torch.as_tensor(t1)
print("result:\n", m(q, k, v))q, k, v = torch.as_tensor(t2), torch.as_tensor(t2), torch.as_tensor(t2)
print("result2:\n", m(q, k , v))

即使调换了qkv顺序，但对b1是没有影响的。

为了引入位置信息，原论文引入了位置编码positional encoding。如下图所示，位置编码是直接加在输入的a={a1,...,an}中的，即pe={pe1,...,pen}和a={a1,...,an}拥有相同维度大小。关于位置编码在原论文有提出两种方案，一种是原论文中使用的固定编码，即论文中给出的sine and cosine funtions方法，按照该方法可计算出位置编码；另一种是可训练的位置编码。ViT论文中使用的是可训练的位置编码。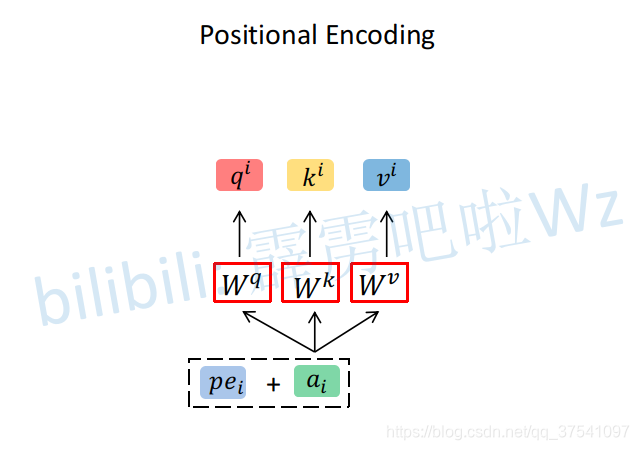 positional encoding