本文主要是介绍(2021,AFT,MHA,RWKV 基础,线性内存复杂度)无注意力的 Transformer,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
An Attention Free Transformer
公和众和号:EDPJ(进 Q 交流群:922230617 或加 VX:CV_EDPJ 进 V 交流群)

目录
0. 摘要
2. 多头注意力(MHA)
3. 方法
3.1 无注意力 Transformer
3.2 AFT 变体:局部性、权重共享和参数化
5. 实验
0. 摘要
我们引入了 Attention Free Transformer(AFT),一种高效的 Transformer变体【1】,消除了点积自注意力的需求。在 AFT 层中,键和值首先与一组学习到的位置偏置(position biases)结合,其结果与查询按元素方式相乘。这种新的操作具有线性内存复杂度,相对于上下文大小和特征维度,使其兼容大输入和大模型规模。我们还引入了 AFT-local 和 AFT-conv,这两个模型变体利用了局部性和空间权重共享的思想,并保持全局连接性(global connectivity)。我们在两个自回归建模任务(CIFAR-10 和 Enwik8)以及一个图像识别任务(ImageNet-1K 分类)上进行了广泛的实验。结果显示,AFT 在所有基准测试中都表现出具有竞争力的性能,同时提供了出色的效率。

2. 多头注意力(MHA)
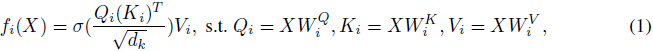
(2023|EMNLP,RWKV,Transformer,RNN,AFT,时间依赖 Softmax,线性复杂度)
3. 方法
3.1 无注意力 Transformer
我们现在定义无注意力 Transformer(AFT),它是多头注意力(MHA)的替代插件,不需要改变 Transformer 的其他架构方面。给定输入 X,AFT 首先将其线性变换为 Q = XW^Q, K = XW^K 和 V = XW^V,然后执行以下操作:
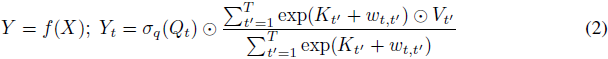
其中,⊙ 是按元素的乘积;σ_q 是应用于查询的非线性函数,默认是 sigmoid;w ∈ R^(TxT) 是学习到的成对位置偏置(见图 2 的说明)。

用语言解释,对于每个目标位置 t,AFT 执行一个加权平均值的计算,其结果与查询按元素相乘。特别地,加权值仅由键和一组学习到的成对位置偏置组成。这提供了不需要计算和存储昂贵的注意力矩阵的直接优势,同时保持了查询和值之间的全局交互,就像 MHA 一样。 为了进一步理解 AFT 与 MHA 的关系,我们可以将公式 2 重新写为:
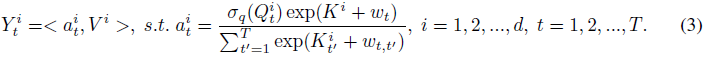
我们在此使用上标 i 来索引矩阵的特征维度;<⋅,⋅> 表示向量的点积。在这种重新排列的形式中,我们能够再次以注意力的形式表达 AFT。具体来说,对于每个位置,我们有一个注意力向量 a^i_t ∈ R^T 用于每个维度,由 Q,K,w 组成。换句话说,AFT 可以解释为对每个特征维度执行隐式注意力,其中注意力矩阵采取因式分解的形式。
3.2 AFT 变体:局部性、权重共享和参数化
AFT-full:我们将定义在公式 2 中的基本版本 AFT 称为 AFT-full。
AFT-local:在许多应用中,局部性是一个重要的归纳偏差,已被 CNN 和最近在 Transformer 中的工作所利用。此外,我们发现训练后的标准 Transformer 往往表现出广泛的局部注意力模式。具体来说,我们可视化了一个经过预训练的 ImagenetNet Vision Transformer (ViT),它由 12 层组成,每层有 6 个头。为了便于可视化,我们忽略了分类标记,并将每层的注意力张量重塑为 6 × 196 × 196 的形状(ViT 的特征图的空间大小为 14 × 14)。然后,我们从 ImageNet 验证集中抽样了 256 张图像。对于每一层和每一个头,我们计算平均相对 2d 注意力,在查询位置(query positions)和图像之间取平均。这产生了一组大小为 12 × 6 × 27 × 27 的注意力图。(12 是层数,6 是头数,27 × 27 是由 14 × 14 特征图生成的相对 2D 注意力的大小)
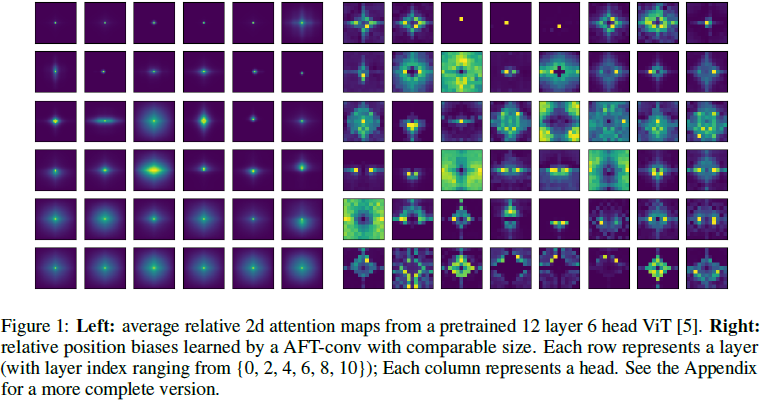
结果显示在图 1(左)中,我们展示了每 2 层的注意力(完整的可视化见附录)。我们看到,相对注意力图显示出强烈的局部模式(如锐度所示),尤其是在较低层。这激发了一种 AFT 的变体,称为 AFT-local,其中我们仅在局部应用一组学习到的相对位置偏差:
![]()
其中,s<T 是一个局部窗口大小。AFT-local 提供了进一步的计算节省,无论是在参数数量还是时间/空间复杂度方面。注意,与局部 Transformer(例如,[7])不同,AFT-local 无论窗口大小 s 都保持全局连接性(global connectivity)。在实验中,我们验证了这一设计选择的有效性。
AFT-simple:AFT-local 的一种极端形式是当 s = 0 时,即没有位置偏差被学习到。这产生了一种非常简单的 AFT 版本,其中我们有:
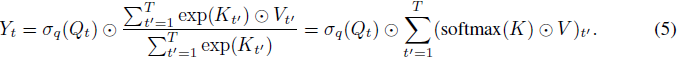
在这个版本中,语境简化(context reduction)进一步简化为逐元素操作和全局池化。AFT-simple 类似于线性注意力【11, 13, 14】,其公式为:Y_t =
![]()
然而,很容易看出,AFT-simple 完全摆脱了点积操作的需求,这使得其复杂度为 O(Td) 而不是O(Td^2)。
AFT-conv:我们还可以进一步扩展局部性的概念,以包含空间权重共享,即卷积。这种变体尤其与视觉任务相关,因为通常希望将预训练模型扩展到可变大小的输入。具体来说,我们让 w_(t,t') 的值仅依赖于 t 和 t' 的相对位置,对应于给定的空间网格(1d 或 2d)。类似于 CNN,我们还可以学习多组位置偏差(我们借用 “头” 的概念以便参考)。为了应对随着头数增加而增长的参数数量,我们采用了一种设计选择,即将 K 的维度与头数绑定。这使得 AFT-conv 可以依赖于深度可分离卷积、全局池化和逐元素操作来实现。
我们现在展示一个具有 1d 输入的 AFT-conv 的示例,2d 和 3d 输入可以类似地推导。我们将模型配置表示为 AFT-conv-h-s,其中 h 是头数,s 是 1d 局部窗口大小。我们现在有 w ∈ R^(h x s),Q, V ∈ R^(T x h x d/h),K ∈ R^(T x h)。对于每个头 (i = 1, 2, ..., h),我们有:
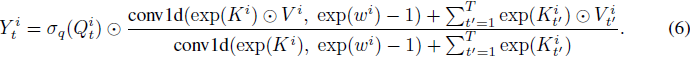
![]()
其中 conv1d(x, w) 是一种深度可分离(depth-wise separable)的一维卷积操作,其中卷积滤波器 w 在通道维度上共享。注意,公式 (6) 可以被解释为一个特定的卷积层,具有以下特点:1) 全局连接性,2) 非负卷积权重,3) 复杂的除法/乘法门控机制。实验表明,这三个方面对 AFT-conv 的性能贡献显著。
参数化。实验证明,适当地参数化位置偏置 w 非常重要。对于 AFT-full 和 AFT-local,我们采用 w 的因子化形式:
![]()
其中 d' 是一个小的嵌入维度(例如 128)。这种简单的因子化不仅极大地减少了参数数量( 2Td' 对比 T^2),而且在训练和测试中均显著提高了模型的性能。
对于 AFT-conv,因子化技巧不可适用。我们采用了一种简单的重新参数化方法,对于每个头 i,我们令
![]()
其中 γ,β ∈ R^h 是可学习的增益和偏置参数,初始值均为 0。
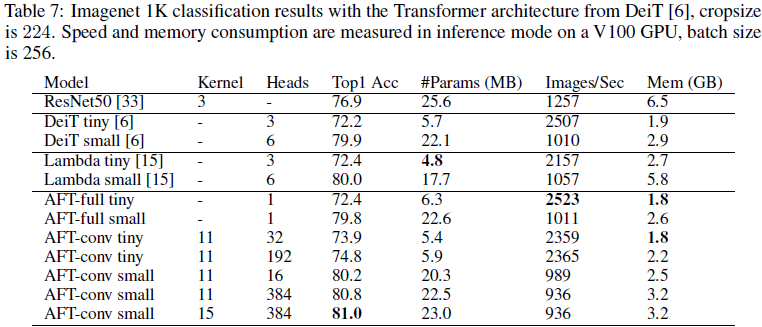
5. 实验
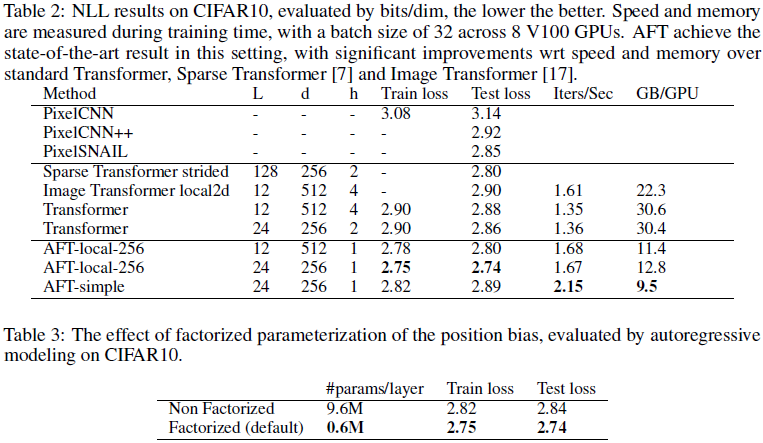
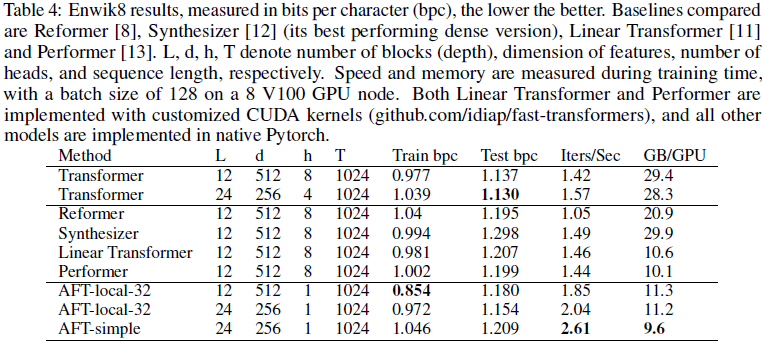



这篇关于(2021,AFT,MHA,RWKV 基础,线性内存复杂度)无注意力的 Transformer的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






