1035专题

代码随想录算法训练营四十三天|1143.最长公共子序列、1035.不相交的线、53.最大子序和、392.判断子序列

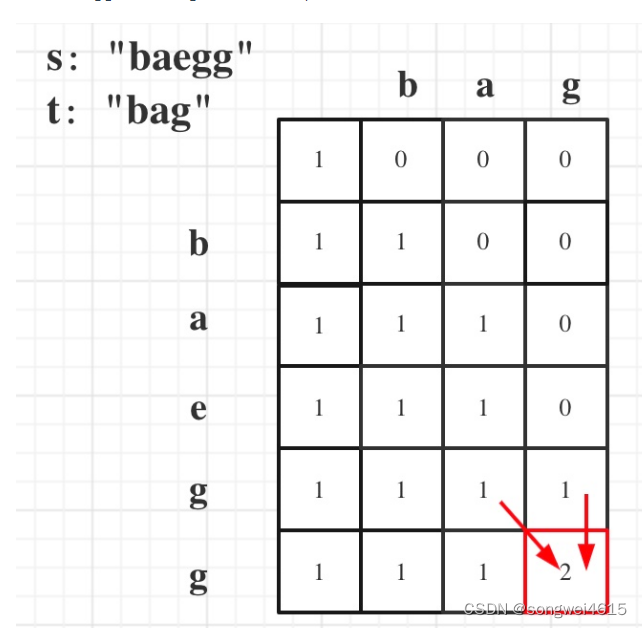
题目链接：1143. 最长公共子序列 - 力扣（LeetCode）思路：如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1; 如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列和 t

每日一题——Python实现PAT甲级1035 Password（举一反三+思想解读+逐步优化）

一个认为一切根源都是“自己不够强”的INTJ 个人主页：用哲学编程-CSDN博客专栏：每日一题——举一反三Python编程学习Python内置函数 Python-3.12.0文档解读目录我的写法代码逻辑分析：时间复杂度分析：空间复杂度分析：我要更强哲学和编程思想举一反三题目链接我的写法 N = int(input()) # 输入用户账

题目1035：找出直系亲属

题目描述：如果A，B是C的父母亲，则A，B是C的parent，C是A，B的child，如果A，B是C的（外）祖父，祖母，则A，B是C的grandparent，C是A，B的grandchild，如果A，B是C的（外）曾祖父，曾祖母，则A，B是C的great-grandparent，C是A，B的great-grandchild，之后再多一辈，则在关系上加一个great-。输入：

【算法刷题day53】Leetcode：1143. 最长公共子序列、1035. 不相交的线、53. 最大子数组和

文章目录 Leetcode 1143. 最长公共子序列解题思路代码总结 Leetcode 1035. 不相交的线解题思路代码总结 Leetcode 53. 最大子数组和解题思路代码总结草稿图网站 java的Deque Leetcode 1143. 最长公共子序列题目：1143. 最长公共子序列解析：[代码随想录解析](https://programmercarl.c

火车停留 wiki 1035

首先这题N和M都很小，可以往网络流方面想。怎么用网络流搞呢，其实就是按题目描述搞，cost显然就是费用，而每个站台同一时间只能停一辆车，以及总站台数的限制显然就是流量，想到这里基本上脑子里已经有一个大概的模型了。 1.肯定要拆点，因为涉及到时间，不拆点不能处理时间的前后关系。 2.拆点肯定是按火车拆，因为火车可以随意选择剩下的车站，以车站为点显然不方便。以上两点想到之后这

代码随想录算法训练营DAY51|C++动态规划Part12|1143.最长公共子序列、1035.不相交的线、53.最大子序列和

文章目录 1143.最长公共子序列思路CPP代码 1035.不相交的线53.最大子序列和思路CPP代码 1143.最长公共子序列力扣题目链接文章讲解：1143.最长公共子序列视频讲解：动态规划子序列问题经典题目 | LeetCode：1143.最长公共子序列本题其实就跟718.最长重复子数组类似，不要求连续了，但是还是要求相对顺序的。思路确定dp数组下标

九度1035 -树 - 找出直系亲属

这道题目一开始我还以为是并查集，后来发现比并查集简单的多，就是一个家谱树，然后找到两个节点之间的深度差。 #include<stdio.h>int data[30];void make_set(){for(int i=0;i<30;i++)data[i]=-1;}int find(int a,int b){int re=1;while(data[a]!=-1){if(data[a]==b

代码随想录算法训练营第五十三天| 1143.最长公共子序列，1035.不相交的线，53. 最大子序和动态规划

题目与题解 1143.最长公共子序列题目链接：1143.最长公共子序列代码随想录题解：1143.最长公共子序列视频讲解：动态规划子序列问题经典题目 | LeetCode：1143.最长公共子序列_哔哩哔哩_bilibili 解题思路：一开始试图用四层循环暴力法来做，就超时了。看完代码随想录之后的想法这里主要是dp定义跟前

1035. 不相交的线

1035. 不相交的线题目链接：1035. 不相交的线代码如下： //代码与思想与 1143. 最长公共子序列一摸一样class Solution {public:int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {dp[i][j]:长度为[0,i-1]的nums1与长度为[0,j-1]的nums2的最

POJ 1035 Spell checker 字符串

#include <iostream>using namespace std;string dic[10010];string che[60];int dc, cc, flag;void setFile () // 输入{dc = cc = 0;do{dc++;cin >> dic[dc];} while ( dc <= 10000 && dic[dc][0] != '

代码随想录算法训练营第五十三天|1143.最长公共子序列 1035.不相交的线 53. 最大子序和动态规划

1143.最长公共子序列体会一下本题和 718. 最长重复子数组的区别视频讲解：https://www.bilibili.com/video/BV1ye4y1L7CQ https://programmercarl.com/1143.%E6%9C%80%E9%95%BF%E5%85%AC%E5%85%B1%E5%AD%90%E5%BA%8F%E5%88%97.html 题目大意：给定两个字符

代码随想录算法训练营第53天 |1143.最长公共子序列、1035.不相交的线、53. 最大子序和

1143.最长公共子序列体会一下本题和 718. 最长重复子数组的区别视频讲解：动态规划子序列问题经典题目 | LeetCode：1143.最长公共子序列_哔哩哔哩_bilibili 代码随想录 1035.不相交的线其实本题和 1143.最长公共子序列是一模一样的，大家尝试自己做一做。视频讲解：动态规划之子序列问题，换汤不换药 | LeetCode：1035.

1035：等差数列末项计算--信息学一本通（c++）

NOIP信息学奥赛资料下载时间限制: 1000 ms 内存限制: 65536 KB 提交数: 13232 通过数: 10290 【题目描述】给出一个等差数列的前两项a1，a2，求第n项是多少。【输入】一行，包含三个整数a1，a2，n。−100≤a1,a2≤100，0<n≤1000。【输出】一个整数，即第n项的值。【输入样例】 1 4 100 【输出样例】 298 【来源】 N

题目 1035: [编程入门]自定义函数之字符类型统计

一、题目题目描述编写一函数，由实参传来一个字符串，统计此字符串中字母、数字、空格和其它字符的个数，在主函数中输入字符串以及输出上述结果。只要结果，别输出什么提示信息。输入格式一行字符串输出格式统计数据，4个数字，空格分开。样例输入 !@#$%^QWERT 1234567 样例输出 5 7 4 6 二、代码 package dotcpp3数组;import j

算法学习——LeetCode力扣动态规划篇9（1035. 不相交的线、53. 最大子数组和、392. 判断子序列、115. 不同的子序列）

算法学习——LeetCode力扣动态规划篇9 1035. 不相交的线 1035. 不相交的线 - 力扣（LeetCode）描述在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足： nums1[i] == nums2[j] 且绘制的直线不与任何其他连线（

一本通1035：等差数列末项计算

1035：等差数列末项计算时间限制: 1000 ms 内存限制: 65536 KB 提交数: 38450 通过数: 29092 【题目描述】给出一个等差数列的前两项a1，a2求第n项是多少。【输入】一行，包含三个整数a1，a2，n。−100≤a1,a2≤100，0<n≤1000。【输出】一个整数，即第n项的值。【输入样例】

代码随想录算法训练营第五十三天|动态规划|1143.最长公共子序列、1035.不相交的线、53. 最大子序和

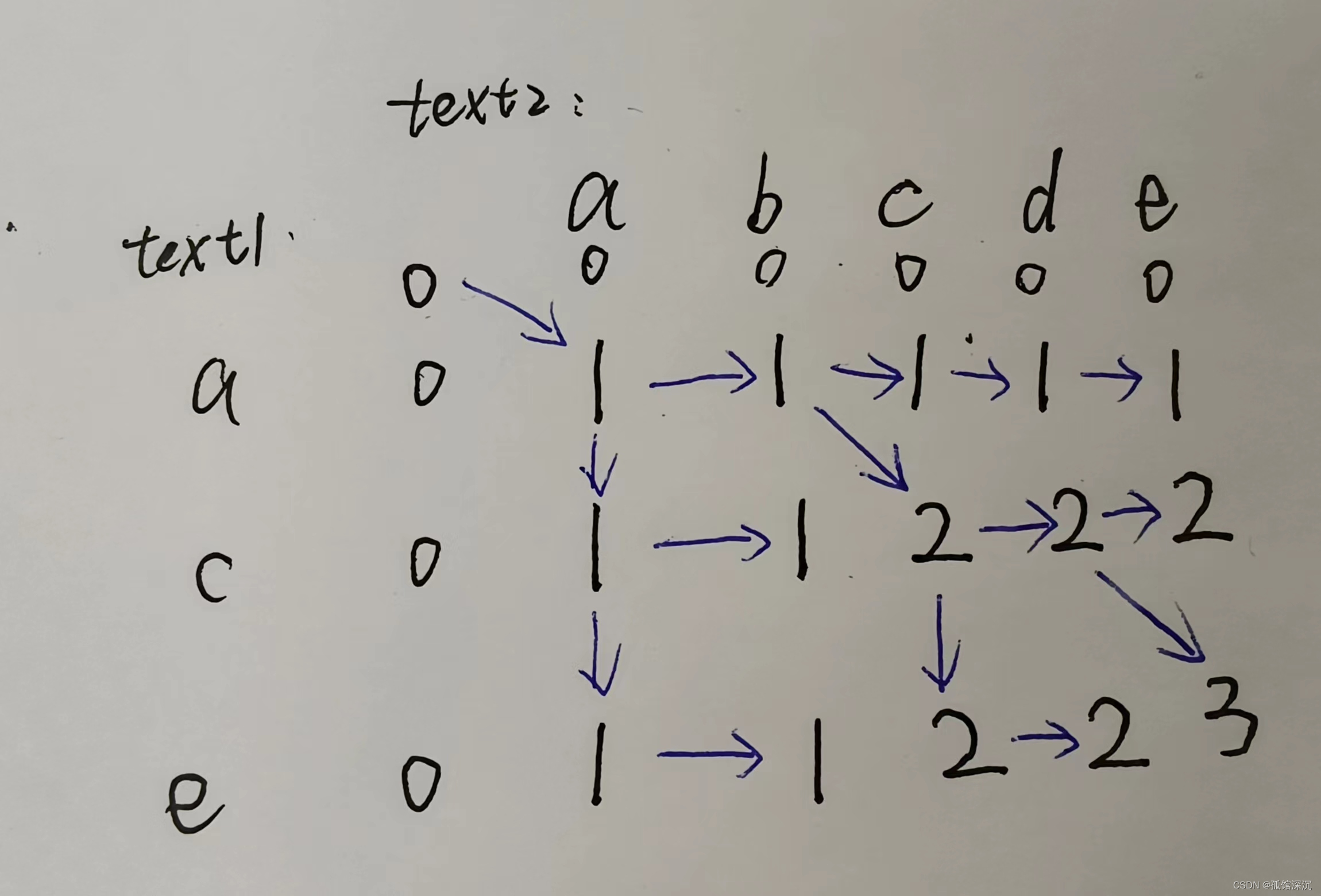
1143.最长公共子序列文章给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。例如，“ace” 是 “abcde” 的子序列，但 “aec” 不是 “abcde” 的子序列。两个字符串的「公共子序列」是这两

代码随想录算法训练营第五十三天｜1143.最长公共子序列 1035.不相交的线 53. 最大子序和

1143.最长公共子序列 https://leetcode.com/problems/longest-common-subsequence/ 思路： longest common subsequence 是动态规划中的经典问题。记住如果 str1[i] == str2[j] dp[i+1][j+1]= dp[i][j] + 1, 不等的话 dp[i+1][j+1] = max(dp[i]

代码随想录算法训练营第53天 | 1143.最长公共子序列，1035.不相交的线，53. 最大子序和

动态规划章节理论基础： https://programmercarl.com/%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80.html 1143.最长公共子序列题目链接：https://leetcode.cn/problems/longest-common-subsequence/descri

力扣● 1143.最长公共子序列 ● 1035.不相交的线 ● 53. 最大子序和动态规划

● 1143.最长公共子序列 1.dp数组含义。 dp[i][j]：数组1[0,i-1]范围的子数组和数组2[0,j-1]的子数组的公共子序列最长长度。注意这里不需要一定以A[i-1]/B[j-1]结尾，原因在下面有说明。动态规划求子序列的问题，一般都是dp的下标相对于数组的下标偏移1，dp[i][j]对应A[i-1]和B[j-1]。 2.递推公式。既然是公共子序列，如果A[i-1]

第五十三天| 1143.最长公共子序列、1035.不相交的线、53. 最大子序和

Leetcode 1143.最长公共子序列题目链接：1143 最长公共子序列题干：给定两个字符串 text1 和 text2，返回这两个字符串的最长公共子序列的长度。如果不存在公共子序列，返回 0 。一个字符串的子序列是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。例如，"ace" 是 "abcde

2021-12-30 1035. 不相交的线（动态规划）

注：题目：在两条独立的水平线上按给定的顺序写下 nums1 和 nums2 中的整数。现在，可以绘制一些连接两个数字 nums1[i] 和 nums2[j] 的直线，这些直线需要同时满足满足： nums1[i] == nums2[j]且绘制的直线不与任何其他连线（非水平线）相交。请注意，连线即使在端点也不能相交：每个数字只能属于一条连线。以这种方法绘制线条，并返回可以绘制的最大

1035 插入与归并

根据维基百科的定义：插入排序是迭代算法，逐一获得输入数据，逐步产生有序的输出序列。每步迭代中，算法从输入序列中取出一元素，将之插入有序序列中正确的位置。如此迭代直到全部元素有序。归并排序进行如下迭代操作：首先将原始序列看成 N 个只包含 1 个元素的有序子序列，然后每次迭代归并两个相邻的有序子序列，直到最后只剩下 1 个有序的序列。现给定原始序列和由某排序算法产生的中间序列，请你判断该

代码随想录算法训练营第四十六天|1143.最长公共子序列，1035.不相交的线，53. 最大子序和

系列文章目录代码随想录算法训练营第一天|数组理论基础，704. 二分查找，27. 移除元素代码随想录算法训练营第二天|977.有序数组的平方，209.长度最小的子数组，59.螺旋矩阵II 代码随想录算法训练营第三天|链表理论基础，203.移除链表元素，707.设计链表，206.反转链表代码随想录算法训练营第四天|24. 两两交换链表中的节点，19.删除链表的倒数第N个节点，面试题 02

Day 53 |● 1143.最长公共子序列 ● 1035.不相交的线 ● 53. 最大子序和

1143.最长公共子序列 class Solution {public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size()+1,vector<int>(text2.size()+1,0));int res = 0;for(int i = 1; i <=

代码随想录算法训练营day53 | 1143.最长公共子序列、1035.不相交的线、53. 最大子序和

1143.最长公共子序列 1、确定dp数组以及下标的含义长度为[0, i-1]的字符串text1与长度为[0, j-1]的字符串text2的最长公共子序列为dp[i][j] 2、确定递推公式主要就是两大情况： text1[i - 1] 与 text2[j - 1]相同，text1[i - 1] 与 text2[j - 1]不相同如果text1[i - 1] 与 text2[j -