本文主要是介绍力扣● 1143.最长公共子序列 ● 1035.不相交的线 ● 53. 最大子序和 动态规划,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
● 1143.最长公共子序列
1.dp数组含义。
dp[i][j]:数组1[0,i-1]范围的子数组和数组2[0,j-1]的子数组的公共子序列最长长度。注意这里不需要一定以A[i-1]/B[j-1]结尾,原因在下面有说明。
动态规划求子序列的问题,一般都是dp的下标相对于数组的下标偏移1,dp[i][j]对应A[i-1]和B[j-1]。
2.递推公式。
既然是公共子序列,如果A[i-1]==B[j-1] ,和● 300.最长递增子序列 一样,dp[i][j]应该在上一个公共子序列的基础上+1,那么上一个最长的公共子序列是哪一个,如果是dp[i][j]的定义是以A[i-1]/B[j-1]为结尾的子序列,那么要求上一个最长的公共子序列,dp[][]的两个下标有可能是[0,i-1]和[0,j-1]的任何一个值,所以这时两层循环里面还要有两层循环,肯定会超时。
所以按照dp[i][j]正确的定义,如果A[i-1]==B[j-1]的话,上一个最长的公共子序列就是dp[i-1][j-1]代表的,所以dp[i][j]=dp[i-1][j-1]+1。
如果不相等的话,不能直接跳过,比如abcde,ace,到了abc、ace的时候c!=e,那么dp[3][3]按照定义应该是2,等于dp[3][2]。把abc、ace倒过来,dp[3][3]又=dp[2][3]。A[i-1]和B[j-1]不相等,但是A[i-1]可能和B[j-1]之前的相等,B[j-1]可能和A[i-1]之前的相等,所以要取这两种情况的最大值。
so:
if(text1[i-1]==text2[j-1]){ //i-1/j-1可以加入,长度加1dp[i][j]=dp[i-1][j-1]+1;
}
else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);//2种情况3.初始化。同样是dp[i][j]代表数组1的前i个和数组2的前j个的比较情况,所以第一行第一列都初始化为0.
4.遍历顺序。同样是i、j从1开始。
5.打印。
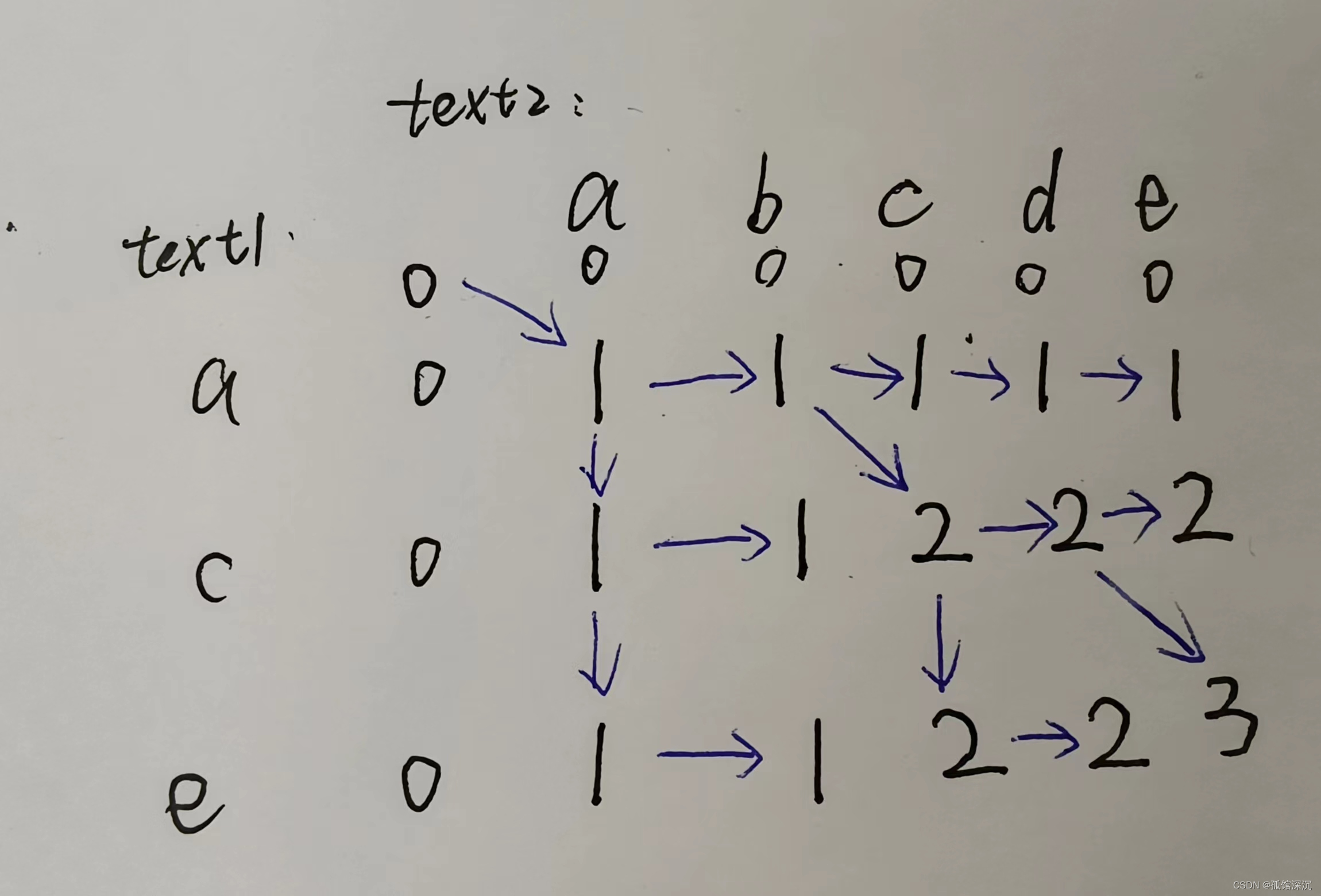
代码:
class Solution {
public:int longestCommonSubsequence(string text1, string text2) {int n1=text1.size();int n2=text2.size();vector<vector<int>> dp(n1+1,vector<int>(n2+1,0));for(int i=1;i<=n1;++i){for(int j=1;j<=n2;++j){if(text1[i-1]==text2[j-1]){ //i-1/j-1可以加入,长度加1dp[i][j]=dp[i-1][j-1]+1;}else dp[i][j]=max(dp[i-1][j],dp[i][j-1]);//2种情况}}return dp[n1][n2];}
};摘自动态规划子序列问题经典题目 | LeetCode:1143.最长公共子序列_哔哩哔哩_bilibili文无cc_评论:
之前的题目,dp代表的序列都是要以[i-1]/[i]结尾求递增序列的时候,即都要确定最后一个元素是谁。
● 300.最长递增子序列 因为要求序列有序,所以必须确定序列最后一个元素的值,才能比较新加入序列的元素是不是递增的。● 674. 最长连续递增序列 和 ● 718. 最长重复子数组 求相等序列的时候,如果求连续相等子序列,则还是要确定序列最后一个元素的值;但是本题求的是不必连续的相等子序列,就不需要知道序列最后一个元素的值,只要知道范围内相等的序列长度就行,新来的相等元素可以直接加在序列后面。
● 1035.不相交的线
上一题所要求的公共子序列,因为这个公共子序列指的是相对顺序不变,如果把这个子序列里面相等的元素A[i]和B[j]连接起来,要么是垂直,要么向一个方向偏斜,不会有相交的情况发生。所以可以绘制的最大连线数其实就是公共子序列的最大长度。
代码随想录:看到代码大家也可以发现其实就是求两个字符串的最长公共子序列,但如果没有做过1143.最长公共子序列,本题其实还有很有难度的。这是Carl为什么要先讲上题再讲本题,大家会发现一个正确的刷题顺序对算法学习是非常重要的!上题是源题,这题是应用,需要转换。
转换的能力很重要,否则看见差不多的题目还是做不出来,要学会举一反三。
● 53. 最大子序和 动态规划
这篇关于力扣● 1143.最长公共子序列 ● 1035.不相交的线 ● 53. 最大子序和 动态规划的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







