子序专题

代码随想录算法训练营四十三天|1143.最长公共子序列、1035.不相交的线、53.最大子序和、392.判断子序列

题目链接：1143. 最长公共子序列 - 力扣（LeetCode）思路：如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1; 如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列和 t

力扣52-最大子序和（java详细题解）

题目链接：https://leetcode.cn/problems/maximum-subarray/description/ 前情提要：因为本人最近都来刷贪心类的题目所以该题就默认用贪心方法来做。贪心方法：局部最优推出全局最优。如果一个题你觉得可以用局部最优推出全局最优，并且没有反例来反驳的话就可以用贪心来试试。题目思路：我们首先要找出局部最优。该题是求最大的子数组和。

【力扣LeetCode】53 最大子序和

题目描述（难度易）给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。示例: 输入: [-2,1,-3,4,-1,2,1,-5,4], 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。进阶: 如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。链接 https://leetcode-c

代码随想录算法训练营第29天（贪心）|455.分发饼干、376. 摆动序列、53. 最大子序和

455.分发饼干题目链接：455.分发饼干文档讲解：代码随想录状态：so easy 思路：对胃口和饼干大小排序，小胃口对应小饼干，不满足的话用下一块饼干试探。题解： public int findContentChildren(int[] g, int[] s) {Arrays.sort(g);Arrays.sort(s);int count = 0;int i

golang最大子序和

题面给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。示例: 输入: [-2,1,-3,4,-1,2,1,-5,4]输出: 6解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。分析比较老实的方法，计算所有可能的子序和，取最大值 O(M*N)问题本质在于若干个子序和可能需要被重置，即确定重写的时机这样只有O(N)若

day31贪心算法part01| 理论基础 455.分发饼干 376. 摆动序列 53. 最大子序和

**455.分发饼干 ** 视频讲解 | 力扣链接刚开始想到的，但是这样太暴力了，太笨了 class Solution {public:int findContentChildren(vector<int>& g, vector<int>& s) {// 胃口g 饼干尺寸sint result = 0;sort(s.begin(), s.end());sort(g.begin(), g.

【代码随想录】【算法训练营】【第32天】 [122]买卖股票的最佳时机II [376]摆动序列 [53]最大子序和

前言思路及算法思维，指路代码随想录。题目来自 LeetCode。 day 32，一个不上班的周六，坚持一了一点~ 题目详情 [122] 买卖股票的最佳时机II 题目描述 122 买卖股票的最佳时机II 解题思路前提：单链表 + 删除元素思路：单链表删除操作，返回新的头节点。重点：考虑是否使用虚拟头结点，如果不适用虚拟头结点，需要单独处理头节点为删除元素的情况，所以建议

【代码随想录】【算法训练营】【第31天】 [455]分发饼干 [376]摆动序列 [53]最大子序和

前言思路及算法思维，指路代码随想录。题目来自 LeetCode。 day 31，放假前的周五，总是令人激动的~ 题目详情 [455] 分发饼干题目描述 455 分发饼干解题思路前提：思路：贪心算法，小饼干优先满足较小胃口。重点：局部最优解，叠加整体最优解。代码实现 C语言排序后，小饼干优先小胃口 int cmp(void *p1, void *p2)

代码随想录算法训练营day31|455.分发饼干、376.摆动序列、53.最大子序和

分发饼干 455. 分发饼干 - 力扣（LeetCode）贪心算法，让每个饼干给到能够满足的孩子，所以需要对饼干尺寸和孩子的满足值先进行排序，然后针对每一个饼干的尺寸，挑选恰好能够满足的孩子（这里表述可能不准确，即从大到小，都选择能够满足的孩子，满足后结果返回值加1），这里选用while循环比较简单，具体代码如下。 class Solution {public:int findConte

代码随想录第三十一天打卡|455.分发饼干，376. 摆动序列， 53. 最大子序和，

455.分发饼干代码随想录 class Solution {public:int findContentChildren(vector<int>& g, vector<int>& s) {sort(g.begin(),g.end());sort(s.begin(),s.end());int left=0,res=0;for (int right=0;right<s.size();rig

leetcode(js) 53. 最大子序和

最大子序和给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。示例: 输入: [-2,1,-3,4,-1,2,1,-5,4], 输出: 6 解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。进阶: 如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。解题思路：直接遍历一遍，因为是连续的，所以只需要保持当

代码随想录-算法训练营day53【动态规划14：最长公共子序列、不相交的线、最大子序和(动态规划)】

代码随想录-035期-算法训练营【博客笔记汇总表】-CSDN博客第九章动态规划part14● 1143.最长公共子序列 ● 1035.不相交的线 ● 53. 最大子序和动态规划详细布置 1143.最长公共子序列体会一下本题和 718. 最长重复子数组的区别视频讲解：https://www.bilibili.com/video/BV1ye4y1L7CQhttps

【Leetcode 53】最大子序和

题目描述方法一：采用贪心法，判断每次和是否大于0 class Solution {public int maxSubArray(int[] nums) {int ans = nums[0];int sum = 0;for(int num: nums) {if(sum > 0) {sum += num;} else {sum = num;}ans = Math.max(ans, sum);}r

代码随想录算法训练营day34 | 455.分发饼干、376. 摆动序列、53. 最大子序和

理论基础贪心的本质是选择每一阶段的局部最优，从而达到全局最优。刷题或者面试的时候，手动模拟一下感觉可以局部最优推出整体最优，而且想不到反例，那么就试一试贪心。 455.分发饼干 result和j变化一致，可以去除一个 class Solution:def findContentChildren(self, g: List[int], s: List[int]) -> int:# 分配

代码随想录算法训练营第三十四天 | 理论基础、455.分发饼干、376、摆动序列、53.最大子序和

目录理论基础 455.分发饼干思路代码 376.摆动序列思路代码 53.最大子序和思路代码理论基础代码随想录 455.分发饼干代码随想录思路可以是大饼干优先满足大胃口，也可以是小饼干优先满足小胃口。代码 class Solution:def findContentChildren(se

代码随想录算法训练营第五十三天| 1143.最长公共子序列，1035.不相交的线，53. 最大子序和动态规划

题目与题解 1143.最长公共子序列题目链接：1143.最长公共子序列代码随想录题解：1143.最长公共子序列视频讲解：动态规划子序列问题经典题目 | LeetCode：1143.最长公共子序列_哔哩哔哩_bilibili 解题思路：一开始试图用四层循环暴力法来做，就超时了。看完代码随想录之后的想法这里主要是dp定义跟前

【 LeetCode 】53、最大子序和

53.1、题目描述给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。 53.2、代码实现 var maxSubArray = function (nums) {// 定义总和和最大值let sum = 0, max = nums[0];// 遍历数组for (let num of nums) {// 初始化时 num = -2 // 下一

Day 31 贪心算法理论基础 455.分发饼干 376. 摆动序列 53. 最大子序和

贪心算法理论基础贪心算法的本质：选择每一个阶段的局部最优，从而达到系统的整体最优；贪心的套路就是没有套路，最好的策略就是举反例，因为大多数时候并不要求严格证明，只需要得到普遍性结论即可；贪心算法一般分为如下四步：将问题分解为若干个子问题找出适合的贪心策略求解每一个子问题的最优解将局部最优解堆叠成全局最优解做题的时候，只要想清楚局部最优是什么推导出全局最优就够了。

代码随想录算法训练营第五十三天|1143.最长公共子序列 1035.不相交的线 53. 最大子序和动态规划

1143.最长公共子序列体会一下本题和 718. 最长重复子数组的区别视频讲解：https://www.bilibili.com/video/BV1ye4y1L7CQ https://programmercarl.com/1143.%E6%9C%80%E9%95%BF%E5%85%AC%E5%85%B1%E5%AD%90%E5%BA%8F%E5%88%97.html 题目大意：给定两个字符

LeetCode-53 最大子序和

题目描述：思路想法：我们可以从头开始遍历，仍然是数组模块的思想，把遍历指向的当前元素和已经形成的子数组分成两个模块A,B（注意：B模块初始为空）；我们只需要考虑：什么时候舍去B模块的这个大尾巴；在加入A模块时，新的B模块是否大于0；大于0就加入，否则不该加入A。并且B模块在此发生断裂，这时我们需要记住B模块存在过的最大值，然后，继续往后遍历。最后我们得到了很多个 B 模块的最大值，

代码随想录刷题day53｜最长公共子序列不相交的线最大子序和

文章目录 day53学习内容一、最长公共子序列1.1、动态规划五部曲1.1.1、确定dp数组（dp table）以及下标的含义1.1.2、确定递推公式1.1.3、 dp数组如何初始化1.1.4、确定遍历顺序1.1.5、输出结果 1.2、代码二、不相交的线2.1、动态规划五部曲2.1.1、确定dp数组（dp table）以及下标的含义2.1.2、确定递推公式2.1.3、 dp数组如何初始

代码随想录算法训练营第53天 |1143.最长公共子序列、1035.不相交的线、53. 最大子序和

1143.最长公共子序列体会一下本题和 718. 最长重复子数组的区别视频讲解：动态规划子序列问题经典题目 | LeetCode：1143.最长公共子序列_哔哩哔哩_bilibili 代码随想录 1035.不相交的线其实本题和 1143.最长公共子序列是一模一样的，大家尝试自己做一做。视频讲解：动态规划之子序列问题，换汤不换药 | LeetCode：1035.

最长重复子数组，最大子序和，最长公共子序列

三种类似动态规划对比 #include<bits/stdc++.h>using namespace std;class Solution{public:int againMax(vector<int>& num1,vector<int>& num2){vector<vector<int> > dp(num1.size()+1,vector<int>(num2.size()+1,0));//二

代码随想录算法训练营第三十一天|455.分发饼干，376. 摆动序列，53. 最大子序和

贪心算法贪心的本质是选择每一阶段的局部最优，从而达到全局最优。贪心算法没有模板。题目：455.分发饼干假设你是一位很棒的家长，想要给你的孩子们一些小饼干。但是，每个孩子最多只能给一块饼干。对每个孩子 i，都有一个胃口值 g[i]，这是能让孩子们满足胃口的饼干的最小尺寸；并且每块饼干 j，都有一个尺寸 s[j]。如果 s[j]= g[i]，我们可以将这个饼干 j 分配给孩子 i ，

代码随想录｜Day31｜贪心算法 part01｜● 455.分发饼干 ● 376. 摆动序列 ● 53. 最大子序和

455.分发饼干 class Solution: def findContentChildren(self, g: List[int], s: List[int]) -> int: # if not g or not s: 可以没有这句，因为后面index>=0已经涵盖了 # return 0 g.sort()

贪心算法|53.最大子序和

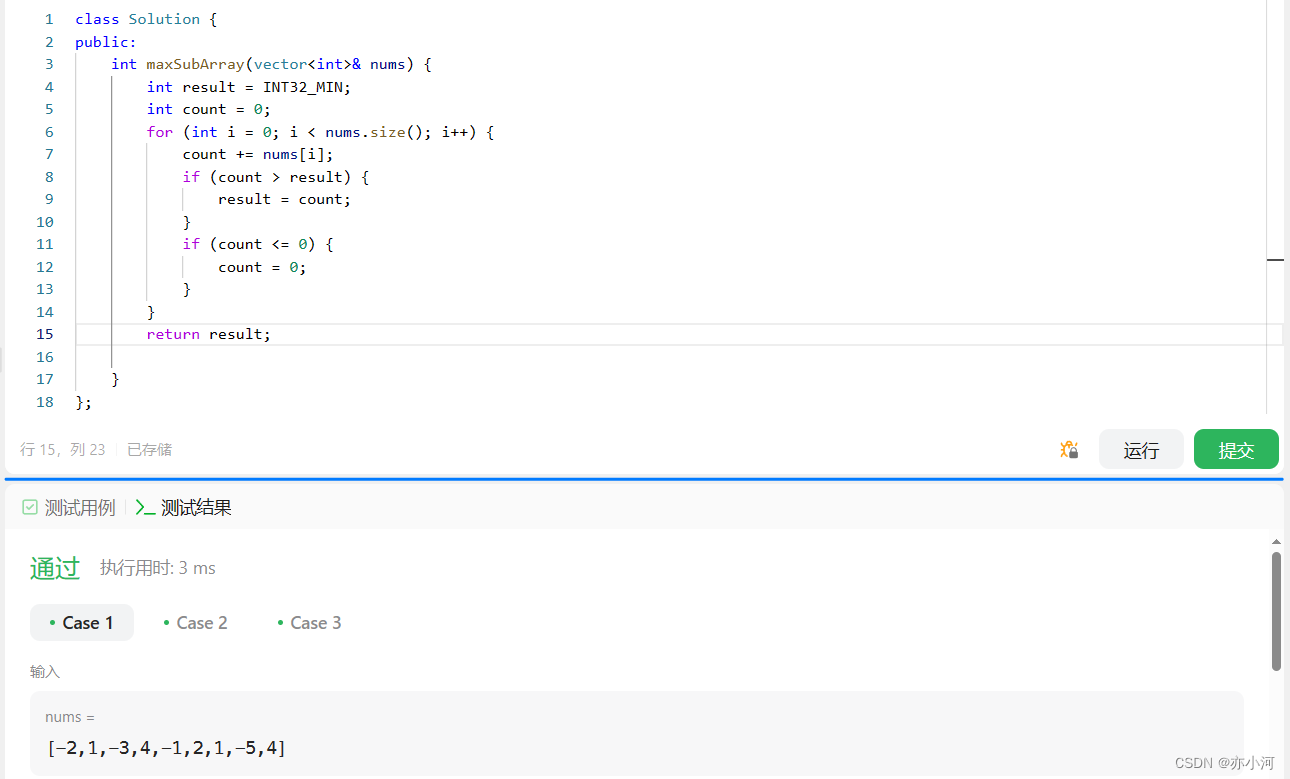
力扣题目链接 class Solution {public:int maxSubArray(vector<int>& nums) {int result = INT32_MIN;int count = 0;for (int i = 0; i < nums.size(); i++) {count += nums[i];if (count > result) {result = count;}if