黑树专题
HashMap 链表转红黑树的阈值为何为 8
与一个重要的统计学原理——泊松分布密切相关:该原理阐明了在单位时间(或面积、体积)内,随机事件的平均发生次数遵循泊松分布 为什么这因子设定为0.5呢? 在忽略方差的情况下,哈希表容量占比的期望值约为 0.5625,也就是说,平均每个桶内有 0.5 个元素,这便是源码中 λ = 0.5 值的由来。
二叉搜索树进阶之红黑树
前言: 在上文我们已经学习了AVL树的相关知识以及涉及的四种旋转的内容,但是AVL树追求平衡导致旋转操作过多,一些情况下影响性能,由此我们就来了解一下二叉搜索树的另外一个分支,红黑树。 (倘若对旋转知识不了解的可以先移步:http://t.csdnimg.cn/waigV) 红黑树的概念: 红黑树是一种二叉搜索树,通过对每个节点增加一个存储位表示节点的颜色,(红色或者黑色),再通过对任何一
什么是红黑树-面试中常问的数据结构
你有没有想过,为什么你的 Java HashMap 能够如此高效地处理数百万个键值对?或者你的 Linux 系统是如何在眨眼间就能管理成千上万的进程的?这些看似神奇的性能背后,隐藏着一个优雅而强大的数据结构 - 红黑树。 目录 什么是红黑树?红黑树的特性为什么需要红黑树?红黑树的结构红黑树的操作插入操作删除操作 红黑树的平衡性分析红黑树的应用场景红黑树 vs AVL树实现一个简单的红黑树红
数据结构十三:2 - 3树和红黑树
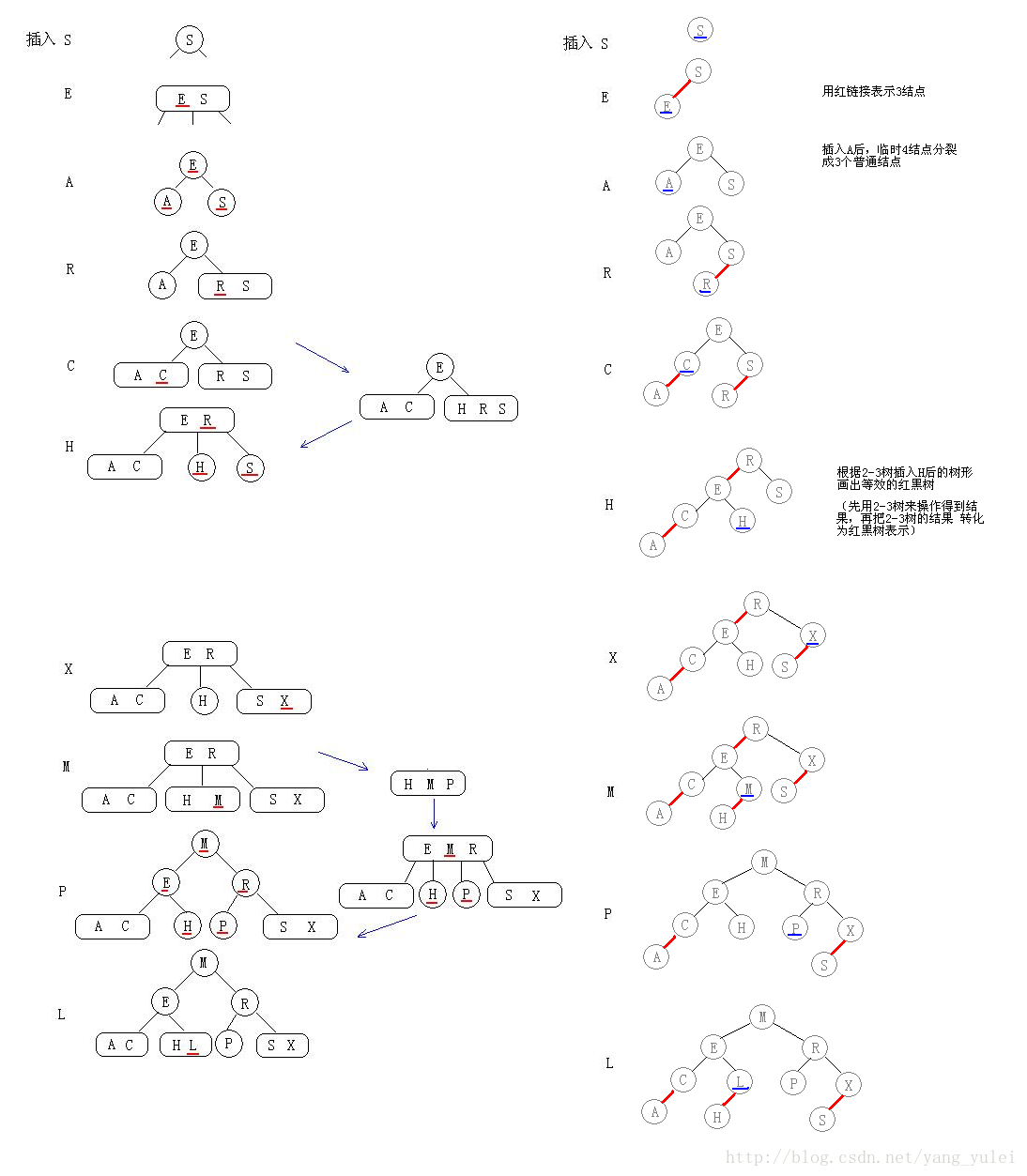
一开始就接触这五点,会让人云里雾里,不利于了解这个数据结构。因为这种先给定义在推导的方式并不适合学习。它没有介绍红黑树的来源,而只是给你生硬的定义。 而学习红黑树的最好学习资料就是大名鼎鼎的《算法4》,如下: Robert Sedgewick 罗伯特 塞奇威克 高德纳的学生。 Donald Knuth 高德纳 : 算法和程序设计技术的先驱者。 2 - 3树和红黑树具有等价
TreeMap源码剖析:自定义排序规则的红黑树map数据结构
文章目录 概述基本结构构造函数自定义排序实现维护红黑树性质小结 概述 Java中的TreeMap类实现了自定义排序规则的红黑树(Red-Black Tree)Map数据结构,它保证了键值对按照键的自然顺序或提供的比较器(Comparator)进行排序。TreeMap实现了NavigableMap接口的有序映射,它使用红黑树数据结构存储键值对。红黑树是一种自平衡的二叉查找树,它通过
哈希表的查找比红黑树更快吗?
这个主要取决于键的类型,因为哈希表需要考虑hash函数和operate==,而红黑树需要考虑operate<。这其中速度取决于hash函数与operate<的计算成本。一般情况下,两者的成本是相同的,因此哈希表查找会比红黑树查找要快。但是,要是考虑有序性操作,这个问题就没有意义了,因为哈希表无法高效的支持这些操作。
数据结构与算法笔记:基础篇 - 红黑树(上):为什么工程中都用红黑树这种二叉树?
概述 上两篇文章,我们依次讲解了树、二叉树、二叉查找树。二叉查找树是最常用的一种二叉树,它支持快速插入、删除、查找操作,各个操作的时间复杂度跟树的高度成正比,理想情况下,时间复杂度是 O ( l o g n ) O(logn) O(logn)。 不过,二叉查找树在频繁的动态更新过程中,可能会出现树的高度远大于 l o g 2 n log_2n log2n 的情况,从而导致哥哥操作的效率下
Leetcode3161. 物块放置查询(Go语言的红黑树 + 线段树)
题目截图 题目分析 每次1操作将会分裂成两块区间长度,以最近右端点记录左侧区间的长度即可 因此涉及到单点更新和区间查询 然后左右侧最近端点则使用redBlackTree,也就是python中的sortedlist ac code type seg []int// 把 i 处的值改成 valfunc (t seg) update(o, l, r, i, val int) {if l =
数据结构复习指导之红黑树
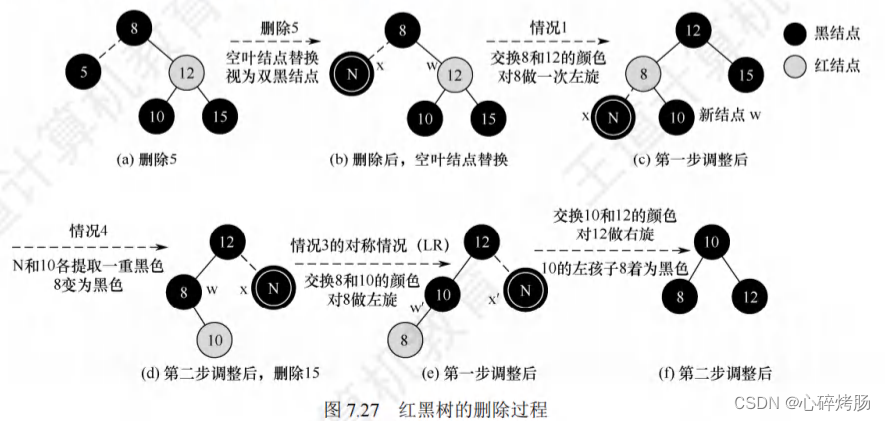
目录 红黑树 考纲内容 知识框架 复习提示 1.红黑树的定义 2.红黑树的插入 3.红黑树的删除 归纳总结 红黑树 考纲内容 (一)查找的基本概念 (二)顺序查找法 (三)分块查找法 (四)折半查找法 (五)树形查找 二叉搜索树;平衡二叉树;红黑树 (六)B树及其基本操作、B+树的基本概念 (七)散列(Hash)表 (八)查找算法的分析及应用
【C++】AVL树和红黑树模拟实现
AVL树和红黑树 1. 背景2. AVL树的概念3. AVL树节点的定义4. AVL树的插入5. AVL树的旋转5.1. 左单旋5.2. 右单旋5.3. 左右单旋5.4. 右左单旋5.5. 旋转总结 6. AVL树的验证7. AVL树的性能8. 红黑树的概念9. 红黑树的节点的定义10. 红黑树的插入10.1. 情况一10.2.情况二 11. 红黑树的验证12. 红黑树与AVL树的比较
从二叉排序树到平衡二叉树再到红黑树系列2
上篇博客主要讲述了二叉排序树的基本概念和插入删除操作,必须再次说明的是:在一棵高度为h的二叉排序树上,实现动态集合操作查询,插入和删除的运行时间均为O(h)。 可见二叉树的基本操作效率取决于树的形态,当然树的高度越低越好,显然树分布越均匀,高度越低。那么,问题来了?对于给定的关键字序列,如何构造一棵形态匀称的二叉排序树。这种匀称的二叉排序树就称为平衡二叉树。 平衡二叉树定义:平衡二叉树或
从二叉排序树到平衡二叉树再到红黑树系列1
最近想写一些关于红黑树的博客,既想写的全面,又直观,但是又不知道从哪里入手。斟酌再三,还是从最简单的二叉排序树开始写。 二叉排序树(Binary Sort Tree)又叫二叉查找树。它是一种特殊结构的二叉树。其或为空树,或具备下列性质: (1)若它的左子树不为空,则左子树上所有结点的值均小于它的根节点的值。 (2)若它的右子树不为空,则左子树上所有结点的值均大于它的根节点的值。 显然,它
HashMap之链表转红黑树(树化 )-treefyBin方法源码解读(所有涉及到的方法均有详细解读,欢迎指正)
PS:由于文档是我在本地编写好之后再复制过来的,有些文本格式没能完整的体现,故提供下述图片,供大家阅览,以便有更好的阅读体验:
B树和二叉排序树(如红黑树)、B树和B+树的区别
B树是为了提高磁盘或外部存储设备查找效率而产生的一种多路平衡查找树。 B+树为B树的变形结构,用于大多数数据库或文件系统的存储而设计。 B树相对于红黑树的区别 在大规模数据存储的时候,红黑树往往出现由于树的深度过大而造成磁盘IO读写过于频繁,进而导致效率低下的情况。为什么会出现这样的情况,我们知道要获取磁盘上数据,必须先通过磁盘移动臂移动到数据所在的柱面,然后找到指定盘面,接
带你手撕红黑树! c++实现 带源码
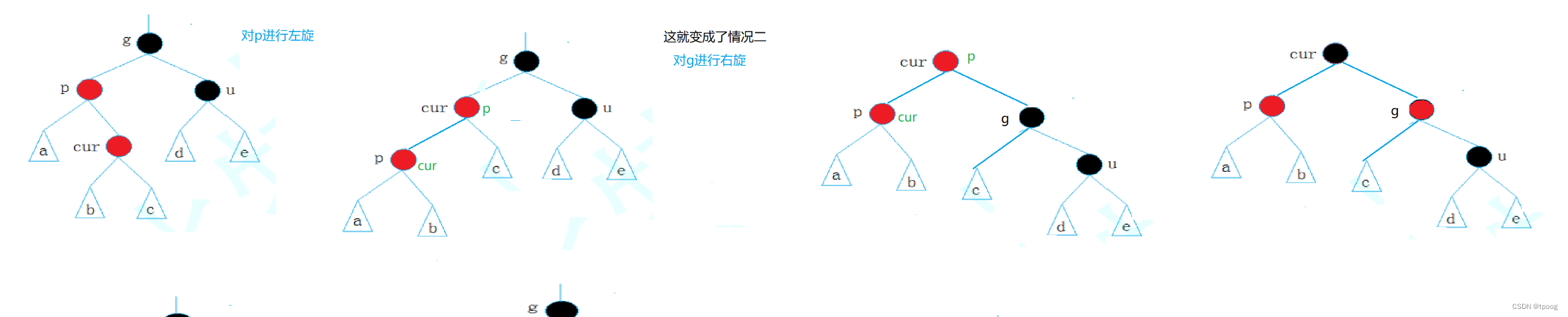
目录 一、概念 二、特性 三、接口实现 1、插入 情况一:p为黑,结束 情况二:p为红 1)叔叔存在且为红色 2)u不存在/u存在且为黑色 (1)p在左,u在右 (2)u在左,p在右 2、检查平衡 四、对红黑树的理解 五、原码 一、概念 红黑树:AVL树不好控制(严格平衡),所以推出了红黑树 不用高度控制平衡,用颜色 最长路径<= 最短路径*2 红黑树是近似平
[C++][数据结构]用红黑树封装map和set(包含红黑树迭代器)
引入 官方文档中,我们可以看到map和set都是用一个红黑树来实现的,那set不给出value、map给出了value,这两个不一样,是如何用一个红黑树来实现的呢? 基本结构 节点的定义 代码中,将pair换成了data template<class T>struct RBTreeNode`在这里插入代码片`{RBTreeNode<T>* _left;RBTreeNode<T>* _
数据结构之红黑树——BST的变种2
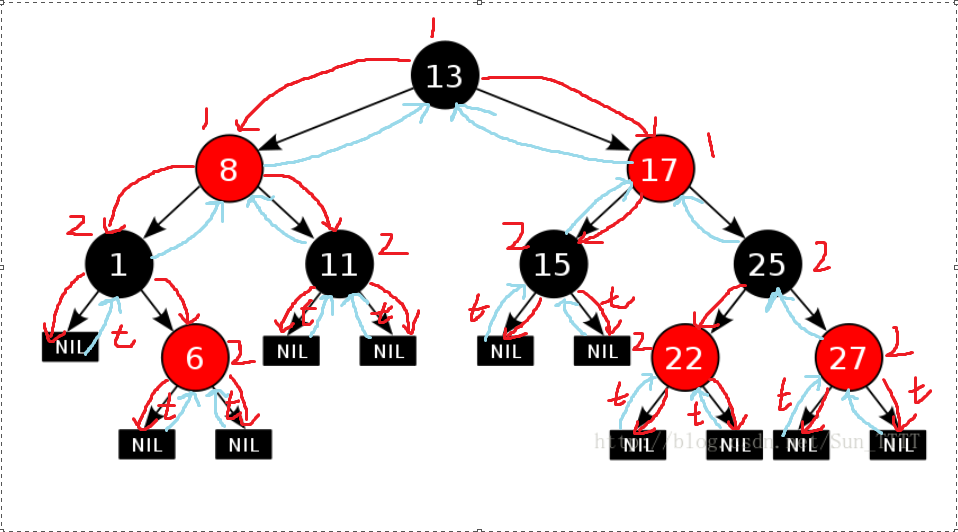
转自:http://hxraid.iteye.com/blog/611816 感谢原文作者的分享 红黑树的性质与定义 红黑树(red-black tree) 是一棵满足下述性质的二叉查找树: 1. 每一个结点要么是红色,要么是黑色。 2. 根结点是黑色的。 3. 所有叶子结点都是黑色的(实际上都是Null指针,下图用NIL表示)。叶子结点不包含任何关键字信
数据结构之红黑树——BST的变种
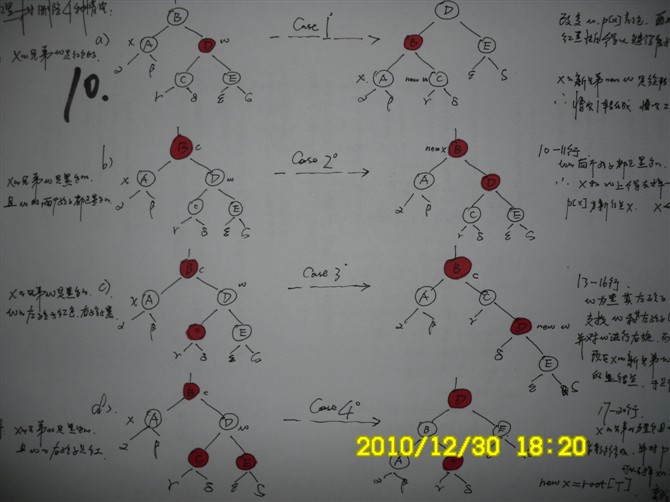
转自大神July的博客:点击打开链接 在此mark一下 教你透彻了解红黑树 作者:July、saturnman 2010年12月29日 本文参考:Google、算法导论、STL源码剖析、计算机程序设计艺术。 推荐阅读: Left-Leaning Red-Black Trees, Dagstuhl Workshop on Data Structures, Wad
面试问你红黑树,你都懂了吗
红黑树(Red Black Tree)是一种自平衡的二叉搜索树(Self-balancing Binary Search Tree)。以前也叫做平衡二叉 B 树(Symmetric Binary B-tree)。 预备知识 树的知识框架结构如下图所示: image 平衡二叉搜索树 平衡二叉搜索树(Balanced Binary Search Tree),英文简称 BBST
查找(一)史上最简单清晰的红黑树讲解
查找(一) 我们使用符号表这个词来描述一张抽象的表格,我们会将信息(值)存储在其中,然后按照指定的键来搜索并获取这些信息。键和值的具体意义取决于不同的应用。 符号表中可能会保存很多键和很多信息,因此实现一张高效的符号表也是一项很有挑战性的任务。 我们会用三种经典的数据类型来实现高效的符号表:二叉查找数、红黑树、散列表。 二分查找 我们
DS进阶:AVL树和红黑树
一、AVL树 1.1 AVL树的概念 二叉搜索树(BST)虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。因此,两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年发明了一种解决上述问题的方法:当向二叉搜索树中插入新结点后,如果能保证每个结点的左右子树高度之差的绝对值不
手撕红黑树(map和set底层结构)(2)
@[TOC]红黑树 一 红黑树概念 红黑树,是一种二叉搜索树,但在每个结点上增加一个存储位表示结点的颜色,可以是Red或Black。 通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。 简单来说红黑树通过了对颜色的控制进而对树的长度做出了限制,不再需要平衡因子。 红黑树性质 每个节点不是红色就是黑色根节点为黑色如果一个节点
排序二叉树,平衡二叉树和红黑树的概念以及相关的操作讲解
1. 排序二叉树 排序二叉树是一种特殊结构的二叉树,可以非常方便地对树中所有节点进行排序和检索。 排序二叉树要么是一棵空二叉树,要么是具有下列性质的二叉树: 若它的左子树不空,则左子树上所有节点的值均小于它的根节点的值;若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;它的左、右子树也分别为排序二叉树。 图 1 显示了一棵排序二叉树: 图 1. 排
【C++】用红黑树封装map和set
我们之前学的map和set在stl源码中都是用红黑树封装实现的,当然,我们也可以模拟来实现一下。在实现之前,我们也可以看一下stl源码是如何实现的。我们上篇博客写的红黑树里面只是一个pair对象,这对于set来说显然是不合适的,所以要想让一个红黑树的代码同时支持map和set,就用上模板就可以了 我们来看看stl源码中是如何实现的 前两个模板参数是两个类型,就是我们要在set或map中
数据结构-AVL树和红黑树的对比
1.红黑树并不追求“完全的平衡”,它只要求达到部分的平衡,降低了对旋转的要求,从而提高了性能。 2.红黑树能够以O(log2 n) 的时间复杂度进行搜索、插入、删除操作,由于它的设计,任何不平衡都会在三次旋转之内解决。 3.还有一些更好的,但实现起来更复杂的数据结构 能够做到一步旋转之内达到平衡,但红黑树能够给我们一个比较“便宜”的解决方案。红黑树的算法时间复杂度和AVL相同,但统计性能比AV










![[C++][数据结构]用红黑树封装map和set(包含红黑树迭代器)](https://img-blog.csdnimg.cn/direct/b2c44d9c1ea0444c9c8d5c1ca8e42b5b.png)