高等专题
【高等代数笔记】线性空间（一到四）
3. 线性空间 令 K n : = { ( a 1 , a 2 , . . . , a n ) ∣ a i ∈ K , i = 1 , 2 , . . . , n } \textbf{K}^{n}:=\{(a_{1},a_{2},...,a_{n})|a_{i}\in\textbf{K},i=1,2,...,n\} Kn:={(a1,a2,...,an)∣ai∈K,i=1,2,...,n
【高等代数笔记】（18）N阶行列式
2. N阶行列式 2.12 行列式按k行（列）展开 【拉普拉斯定理】 n n n阶矩阵 A = ( a i j ) \boldsymbol{A}=(a_{ij}) A=(aij)，取定第 i 1 , i 2 , . . . , i k i_{1},i_{2},...,i_{k} i1,i2,...,ik行（其中 i 1 < i 2 < . . . < i k i_{1}<i_{2}<.
高等代数精解【10】
文章目录 线性方程组概述增广矩阵基础一、增广矩阵的作用二、增广矩阵的实际应用例题 高斯消元法基础julia代码实现高斯消元法算法方阵高斯消元法非方阵的情况 Julia 中将整型矩阵转换为浮点型矩阵。方法 1：使用类型转换函数方法 2：使用 `convert` 函数方法 3：利用矩阵运算或函数方法 4：使用 `map` 函数 参考文献 线性方程组 概述 线性方程组是由一个或
《高等代数》行（列）和相等行列式
说明：此文章用于本人复习巩固，如果也能帮助到大家那就更加有意义了。 注：1）行（列）和相等行列式的求解方法是将其于行都加到第一行（列），然后再提取第一行 （列），使得第一行（列）变成“1”，再用第一行（列）将行列式化为三角形行列式。
《高等代数》范德蒙德行列式的应用
说明：此文章用于本人复习巩固，如果也能帮助到大家那就更加有意义了。 注：范德蒙德行列式的简单应用及其变形。 范德蒙德行列式的计算公式： 注：（1）用大下标减去小下标。 （2）i>j,不是i≥j 例一：（公式的简单应用） 例二：（缺失的范德蒙德行列式一） 注：1）可以看到，所要求的行列式与范德蒙德行列式相比缺失了次数为三次方的一行。利用行列
《高等代数》“爪”字型行列式
说明：此文章用于本人复习巩固，如果也能帮助到大家那就更加有意义了。 注：1）“爪”字型行列式的第一种求解方法是利用初等行（列）变换，将第一列除第一行的第 一个数以外的其它数都化为0，得到三角行列式，然后进行求解。 2）“爪”字型行列式的第二种求解方法是“加边法”，其目的也是最终将行列式化为三角行列式 进行求解。
《高等代数》最大公因式典型例题
说明：此内容用于本人复习巩固，如果也能帮助到大家那就更加有意义了。 注：这道题主要从 1)公因式整除多项式的线性组合 2)最大公因式能够被其它公因式整除 3)如果两个多项式互相整除，那就说明这两个多项式相等 这三个知识点出发进行证明。 首先，等式左边是f(x)与g(x)的最大公因式，等式右边是af(x)+bg(x)与cf(x)+dg(x)的最大公因式，我们分别把它们记作d
湖北民族大学2024年成人高等继续教育招生简章
湖北民族大学，这所承载着深厚文化底蕴和卓越教育理念的学府，在崭新的2024年再次敞开怀抱，热烈欢迎有志于深化学习、提升自我的成人学员们。今年的成人高等继续教育招生，不仅是学校对于终身教育理念的具体实践，更是为广大社会人士提供了一次难得的学习机会。 湖北民族大学，以其悠久的历史、优秀的师资和卓越的教学质量，早已在成人教育领域树立了良好的口碑。学校秉承“博学、博爱、立人、达人”的校训，致力于培养
广东信息工程职业学院2024年成人高等继续教育招生简章
一、学校简介 广东信息工程职业学院位于广东省肇庆市，是一所具有一定办学规模，办学定位和培养目标明确，办学特色和追求鲜明，可持续发展的全日制普通高等学校，学院坚持以人为本，以德育人，以良好的学风、教风和校风，促进学生的全面发展，以“对社会负责、对学生负责、让家长放心、让学生满意”的的良好信誉赢得社会认可。重视德育和人文素质教育，积极为社会培养高技能高素质的适用性人才。 二、招生专业 工程造
鄂州职业大学2024年成人高等继续教育招生简章
鄂州职业大学，作为一所享有盛誉的高等学府，一直以来都致力于为社会培养具备专业技能和良好素养的优秀人才。在成人高等继续教育领域，该校同样表现出色，为广大渴望继续深造、提升自身能力的成年人提供了宝贵的学习机会。 随着社会的快速发展，终身学习的观念深入人心，成人高等继续教育逐渐成为了一种趋势。鄂州职业大学紧跟时代步伐，充分发挥自身优势，不断创新教学模式，提高教育质量，以满足不同领域、不同层次的成人
AI创意广告案例分析️可口可乐、麦当劳、伊利、钟薛高等一线品牌各显神通
AI 相关的教学我们最近做了不少分享，本期计育韬老师则希望和广告人们谈一谈具体的落地案例应用及其内在创意方法论。结合在 Midjourney 频道 LV.14 的部分创作经验，相信能为广大品牌方带来 AI 广告创作的启迪。 担心版权争议？ 那就主打 UGC 共产。 已经介入 AI 内容生产的企业，想必或多或少都还悬着版权层面顾虑之心。虽然就行业内有所耳闻的海外庭审结果来看，
高等代数复习：同构定理
文章目录 同构定理 本篇文章适合个人复习翻阅，不建议新手入门使用 同构定理 接下来我们要证明如下几个同构定理 定理（线性映射同构定理） 设 φ ： V → V ′ \varphi：V\to V' φ：V→V′ 是一个线性映射，则存在一个自然的线性同构 V / ker φ ≅ Im φ V/\ker \varphi \cong \operatorname{Im}
高等代数复习：线性映射
文章目录 线性映射基本定义和记号线性映射与矩阵线性映射的像与核不变子空间 本篇文章适合个人复习翻阅，不建议新手入门使用 线性映射 基本定义和记号 定义：线性映射 设数域 K \mathbb{K} K 上的线性空间 U , V U,V U,V，映射 φ : V → U \varphi:V\to U φ:V→U 满足： φ ( α + β ) = φ ( α )
高等代数复习：矩阵的满秩分解
文章目录 矩阵的满秩分解 本篇文章适合个人复习翻阅，不建议新手入门使用 矩阵的满秩分解 定义：矩阵的左逆、右逆 设 A A A 是 m × n m\times n m×n 矩阵 若 r ( A ) = n r(A)=n r(A)=n，即 A A A 列满秩，则存在秩为 n n n 的 n × m n\times m n×m 行满秩矩阵 B B B，使得
![[足式机器人]Part4 南科大高等机器人控制课 Ch01 Linear Differential Equations and Matrix Exponential](https://img-blog.csdnimg.cn/direct/8be5c97036b544e78a0eee06203358a0.png#pic_center)
[足式机器人]Part4 南科大高等机器人控制课 Ch01 Linear Differential Equations and Matrix Exponential
本文仅供学习使用 本文参考： B站：CLEAR_LAB 课程主讲教师： Prof. Wei Zhang 南科大高等机器人控制课 Ch01 Linear Differential Equations and Matrix Exponential 1. ODEs-Ordinary Differential Equations1.1 Dynamics of 2R linkage1.1.1
国家开放大学2021春1079高等代数专题研究题目
教育 教育 试卷代号：1079 2021年春季学期期末统一考试 高等代数专题研究 试题 2021年7月 一、单项选择题（本题共20分，每小题4分） 1.下列运算中，（ ）是有理数域Q上的代数运算. A.a。b=a B.a。b=b C.a。b=ab D.a。b=a 2.按通常数的加法与乘法，复数域C可以看成实数域R上的线性空间，则它的维教是（ ）. A.0 B.1 C.2 D.无限 3.矩阵A与
辽宁交通职业技术学校计算机好不好,辽宁省交通高等专科学校怎么样 全国排名第几...
辽宁省交通高等专科学校坐落于历史文化名城沈阳，是为新中国交通建设而设立的第一所专门学校。辽宁省交通高等专科学校在全国高职高专院校排行榜中，排名第25位。 2020辽宁省交通高等专科学校排名排名院校名称地区类型序 20成都航空职业技术学院四川8 21芜湖职业技术学院安徽11 22武汉职业技术学院湖北12 23宁波职业技术学院浙江9 24黄河水利职业技术学院河南13 25辽宁省交通高等专科学校辽宁
取得页面的大小 宽高等各种信息
<body><SCRIPT LANGUAGE="JavaScript">function test(){var s = "";s += "/r/n网页可见区域宽："+ document.body.clientWidth;s += "/r/n网页可见区域高："+ document.body.clientHeight;s += "/r/n网页可见区域宽："+ document.body.offset
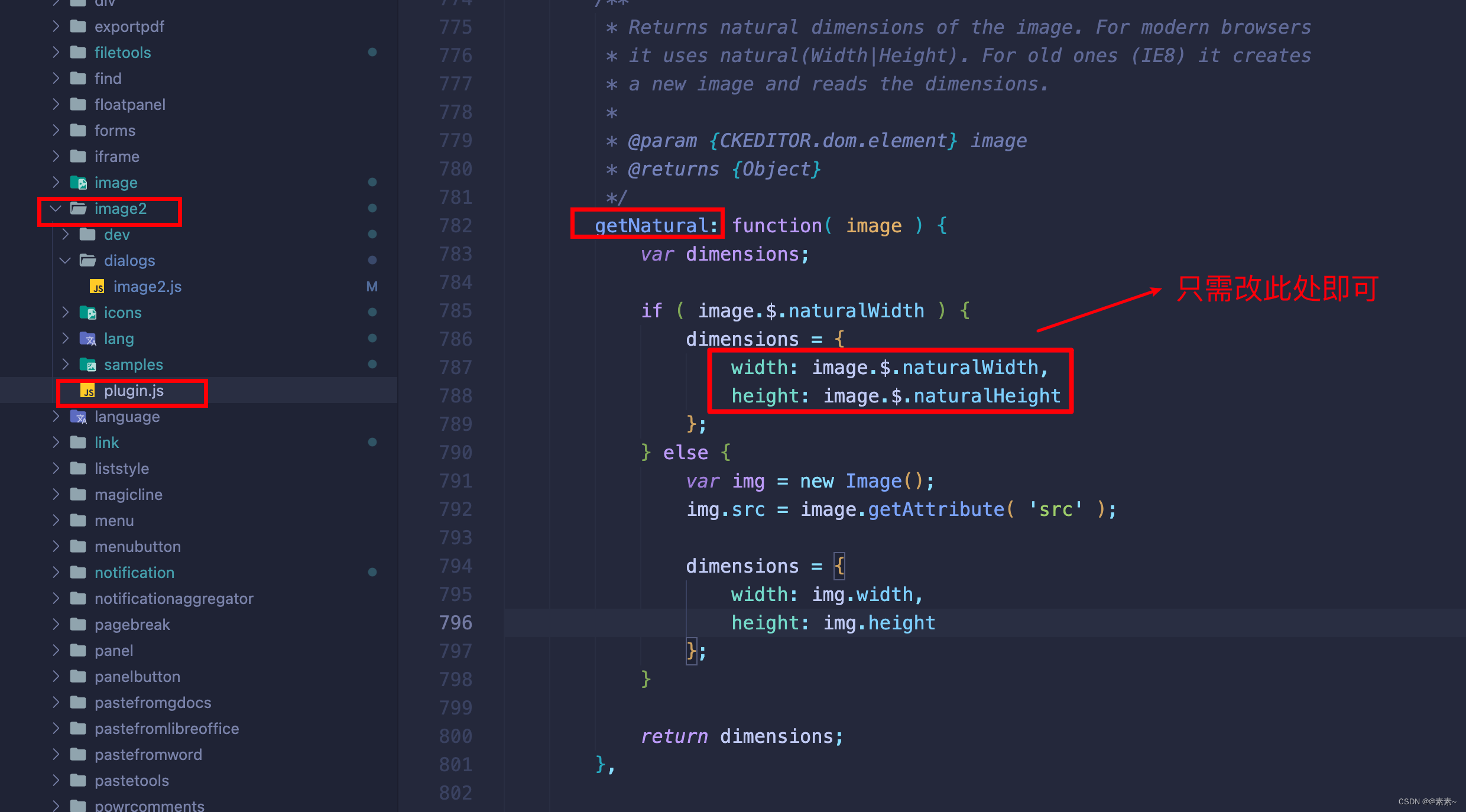
富文本编辑器CKEditor4简单使用-04（跟源码设置image2插件图片的默认宽高等相关配置）
富文本编辑器CKEditor4简单使用-04（跟源码设置image2插件图片的默认宽高等相关配置） 1. 前言1.1 CKEditor4快速上手 2. CKEditor4的一般配置2.1 工具栏相关2.2 插件相关2.3 设置界面宽高等 3. CKEditor4的图片相关配置3.1 关于增强的图像插件的必要配置3.2 隐藏image2插件的上传界面的URL3.2.1 默认界面3.2.2 修改
数学分析高等代数难题选
欢迎关注跟锦数学微信公众号. 可直接搜索”跟锦数学”, 也可扫描网页左上方的二维码. 以后更新也放在跟锦数学微信公众账号. 如果有好的题目或解答 (图片或 tex 代码均可), 愿意共享的话, 一可以回帖 (弄了个论坛 http://math.funbbs.me, 欢迎注册并发言), 二可以发邮件给 zhangzujin361@163.com. 之后在题后给出链接, 给您扬名 (注明您所写的
《高等统计物理学》Cookbook（持续更新）
在《高等统计物理学》系列文章中，有时候会用到一些重要的量子力学基础知识，比如定态薛定谔方程的求解、产生和消灭算符等等。本部分为读者建立一个即用即查的“工具箱”，为方便正文的高效学习。 内容 一. 薛定谔方程求解 二. 消灭算符和产生算符 三. 玻色子、费米子和保、泡利不相容原理 四. 高Tc超导体的主要性质 一. 薛定谔方程求解 1. 求解步骤 （1）分离变量； Ψ ( r , t
《高等统计物理学》5：非平衡态统计物理初步
知乎链接：《高等统计物理学》5：非平衡态统计物理初步 上一篇文章《高等统计物理学》4：量子系综的实际问题 是统计物理系综的最后一个部分，同时也是平衡态统计物理复习的大结局。下面将开始非平衡态统计物理的复习，在这里笔者只是将相关的概率知识进行罗列，更深层次的非平衡态统计物理的内容待笔者考完试有时间自学后再进行相关的大补充。 四. 非平衡态统计物理初步 1. 中心极限定理 考虑随机变量 X的N