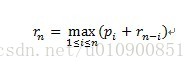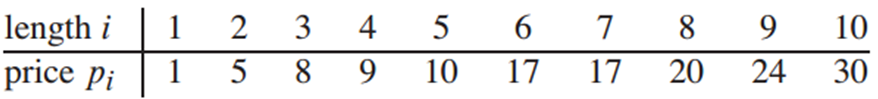钢条专题
切割钢条【动态规划】
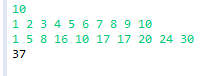
假设公司出售一段长度为i英寸的钢条的价格为Pi(i = 1, 2, ...单位:美元),下面给出了 价格表样例: 长度i 1 2 3 4 5 6 7 8 9 10 价格Pi 1 5 8 9 10 17 17 20 24 30 切割钢条的问题是这样的:给定一段
钢条切割问题的解法(C/C++)
(原题见算法导论·动态规划) 对长度为n的钢条进行切割,对应的切割长度和价格对应如下: int cost[] = {0, 1, 5, 8, 9, 10, 17, 17, 20, 24, 30}; 比如1对应价值1,10对应价值30。即相应的下标和值的对应。现求切割所得最大效益mx。 1.递归算法: //g++ 编译通过int cut_rod(int *cost,int n){i
动态规划之钢条切割问题自底向上发的实现(算法导论第15章)
看算法导论的同学应该知道第15章在讲动态规划,以钢条切割问题作为引论,那么钢条切割问题实际的C代码是怎么实现的呢?图表和题目我就不叙述了,直接看代码 // steercut.cpp : Defines the entry point for the console application.//// 钢条切割问题.cpp : Defines the entry point for the c
算法导论--第15章 动态规划--钢条切割
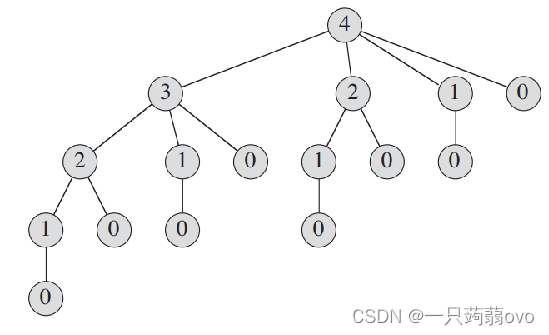
算法导论 --第15章 动态规划 •动态规划:通过组合子问题的解来求解原问题,应用于子问题重叠的情况,即不同的子问题具有公共的子子问题。 •设计动态规划算法的步骤: ① 刻画一个最优解的结构特征。 ② 递归定义最优解的值。 ③ 计算最优解的值,通常采用自底向上的方法。 ④ 利用计算处的信息构造一个最优解。 15.1 钢条切割 钢条切割问题:给定一
动态规划——切割钢条问题
一、动态规划 动态规划算法通常用于解决最优化问题(寻求最优解)。其思想与分治法类似,将待求解的问题分成若干个子问题,先求出子问题,再根据子问题的解求出原来问题中的解,与分支法不同的是,在动态规划中,这些子问题的解是不相互独立的。 采用动态规划求解的问题通常有以下性质: 1.最优化原理:问题的最优解中包含的子问题的解也是最优的。
动态规划算法--斐波拉契数列、钢条切割、小朋友过桥、01背包问题
文章目录 动态规划1.求斐波拉契数列Fibonacci 。2.钢条切割3.小朋友过桥问题4.01背包问题 购物单:有依赖的01背包问题5. 最多路径数6. 编辑距离7. 4 键键盘问题8. leetcode322. 零钱兑换9. leetcode983. 最低票价10. 经典算法题:高楼扔鸡蛋11. leetcode 221. 最大正方形12.leetcode 10. 正则表达式匹配13.
8.11 动态规划例题-----钢条切割(从递归--> 记忆型递归---->动态规划)
题目: 已知钢条总长i 和 每种长度下的钢条价格,让我们找到一种切割方案,使得价格最大 解法一:递归 import java.util.Arrays;import java.util.Scanner;public class Main {/* * 思路:假设钢条长度为L* 依次固定前面的切割点为1....L,计算最大价值* * 测试数据101 2 3 4 5 6 7 8 9 10
代码随想录算法训练营第三十一天丨15.1钢条切割、LCR 126. 斐波那契数/习题15.1-5、53. 最大子数组和
15.1钢条切割 假设你有一根长度为n英寸的钢条和一个价格表,表中列出了不同长度的钢条的售价。你可以选择不同的方式切割这根钢条,然后将切割后的各段钢条按照价格表出售。目标是确定如何切割钢条以使得销售收益最大化。 问题的输入是一个价格表P[i],其中i=1,2,...,n,表示长度为i英寸的钢条的价格,以及钢条的总长度n。问题的输出是最大收益R[n]以及达到这个最大收益时各段钢条的长度。 解
钢条分割 动态规划java_动态规划-钢条切割问题
Description: The rod-cutting problem is the following. Given a rod of length n inches and a table of prices pi for i D 1,2,…,n, determine the maximum revenue rn obtainable by cutting up the rod and s
【算法-动态规划】钢条切割问题
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学习,不断总结,共同进步,活到老学到老导航 檀越剑指大厂系列:全面总结 java 核心技术点,如集合,jvm,并发编程 redis,kafka,Spring,微服务,Netty 等常用开发工具系列:罗列