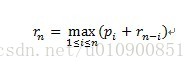本文主要是介绍算法导论--第15章 动态规划--钢条切割,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
算法导论
--第15章 动态规划
•动态规划:通过组合子问题的解来求解原问题,应用于子问题重叠的情况,即不同的子问题具有公共的子子问题。
•设计动态规划算法的步骤:
① 刻画一个最优解的结构特征。
② 递归定义最优解的值。
③ 计算最优解的值,通常采用自底向上的方法。
④ 利用计算处的信息构造一个最优解。
15.1 钢条切割
钢条切割问题:给定一段长度为n英寸的钢条和一个价格表 (i=1,2, …,n),求切割钢条的方案,使得销售收益 最大。注意,如果长度为n英寸的钢条价格 足够大,最饥饿可能就是完全不需要切割。
若钢条的长度为i,则钢条的价格为Pi,如何对给定长度的钢条进行切割能得到最大收益?
长度i 1 2 3 4 5 6 7 8 9 10
价格Pi 1 5 8 9 10 17 17 20 14 30
i = 1时,钢条不可切割,r[1]= 1
i = 2时,钢条可分割为1+ 1,其价格为2。若不分割(0 + 2),价格为5。即r[2] = 5
i = 3时,钢条可分割为0+ 3, 1 + 2。r[3] = 8
同理可得:
r[4] = 10(2+ 2)
r[5] = 13(2+ 3)
r[6] = 17(0+ 6)
r[7] = 18(1+ 6或4+ 3=> 2 + 2 + 3)
.......
我们可以发现,长度为7时,将其切割为长度4与长度3的钢条,并对两个钢条分别求最优解:长度4的最优解为r[4] = 10(2 + 2),长度3的最优解为r[3] = 8,即可得r[7] =r[4]+ r[3] =>原问题的最优解等于子问题的最优解之和的最大值
我们将钢条左边切割下长度为 i 的一段,只对右边剩下的长度为 n-i 的一段继续进行切割(递归求解),对左边的一段不再进行切割。即问题分解的方式为:将长度为n 的钢条分解为左边开始一段,以及剩余部分继续分解的结果。这样,不做任何切割的方案就可以描述为:第一段的长度为n ,收益为 pn,剩余部分长度为0,对应的收益为r0=0。于是公式的简化版本:
因此,在计算r[i]时,所求值即为r[0] +r[i],r[1]+ r[i- 1],r[2]+ r[i- 2],... ,r[i- 1] +r[1] 之间的最大值,而在动态规划中,r[0]——r[i - 1]的值在计算r[i]之前已经保存好了,进行少量的运算便能取得最优结果。
codes:
#include<iostream>
#include<cstring>
using namespace std;
int p[1000],r[1000],s[1000];
void cut_rod(int* a,int b)
{r[0]=0;for(int i=1;i<=b;i++){int q=-1e8;for(int j=1;j<=i;j++){if(q<(a[j]+r[i-j])){q=a[j]+r[i-j];s[i]=j;r[i]=q;}}}cout<<r[b]<<endl<<s[b]<<endl;
}
int main()
{int n;cin>>n;memset(p,0,sizeof(p));memset(r,0,sizeof(r));memset(s,0,sizeof(s));for(int i=1;i<=n;i++)cin>>p[i];cut_rod(p,n);return 0;
}这篇关于算法导论--第15章 动态规划--钢条切割的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!