邻接专题
像素间的关系(邻接、连通、区域、边界、距离定义)
文章目录 像素的相邻像素4邻域D邻域8邻域 邻接、连通、区域和边界邻接类型连通区域边界 距离测度欧氏距离城市街区距离(city-block distance)棋盘距离(chessboard distance) 参考 像素的相邻像素 4邻域 坐标 ( x , y ) (x,y) (x,y)处的像素 p p p有2个水平的相邻像素和2个垂直的相邻像素,它们的坐标是: ( x
「图」邻接矩阵|边集数组|邻接表 / LeetCode 35|33|81(C++)
概述 我们开始入门图论:图的存储。 图是一种高级数据结构:链表是一个节点由一条边指向下一个节点,二叉树是一个节点由两条边指向下两个节点,而图是由任意多个节点由任意多条边指向任意多个节点。 图由节点和边构成,边往往存在边权。边权在不同的问题中往往有不同含义,如在最短路径中表示边的长度,在AOE网中表示任务所需时间。 对于这种复杂的结构,如何存储在计算机的程序语言中呢? 我们先来介绍三种存储
数据结构实验图论:基于邻接矩阵/邻接表的广度优先搜索遍历(BFS)
数据结构实验图论一:基于邻接矩阵的广度优先搜索遍历 Time Limit: 1000MS Memory limit: 65536K 题目描述 给定一个无向连通图,顶点编号从0到n-1,用广度优先搜索(BFS)遍历,输出从某个顶点出发的遍历序列。(同一个结点的同层邻接点,节点编号小的优先遍历) 输入 输入第一行为整数n(0< n <100),表示数据的组数。 对于
判别以邻接表方式存储的有向图中是否存在由顶点vi到顶点vj的路径(i≠j)
试基于图的深度优先搜索策略写一算法,判别以邻接表方式存储的有向图中是否存在由顶点vi到顶点vj的路径(i≠j)。 注意:算法中涉及的图的基本操作必须在此存储结构上实现。 图的邻接表以及相关类型和辅助变量定义如下: Status visited[MAX_VERTEX_NUM];typedef char VertexType;typedef struct ArcNode {int adj
计算多图的等价无向图的邻接链表表示
计算多图的等价无向图的邻接链表表示 摘要:一、引言二、算法思路三、伪代码实现四、C代码实现五、算法分析六、结论 摘要: 在图论中,多图(Multigraph)是一种允许边重复以及存在自循环边(即一个顶点到其自身的边)的图。给定一个多图的邻接链表表示,本文旨在探讨如何构造一个等价的无向图,并给出其邻接链表表示。所谓等价的无向图,指的是在删除所有冗余的边和自循环边后,对于任意两个顶点
有向图的邻接表实现(Java版)
我是蚊子码农,欢饮您的关注。 一、有向图介绍 在无向图中,边没有方向性,就相当于一条公路,你可以来我这,我也可以去你那。 然而,现实世界里,有一些通道是单向的,只允许一个方向通过。 比如某些工作流程,你必须完成工作A,才能进行工作B。 这时候,我们需要用有向边,来表达这些数据。 当然,无向图可以看成特殊的有向图。 二、有向图的表达(思考部分) 我们知道,图是由结点集和边集构成的。其中,每一
(转)图算法单源最短路径Dijkstra算法(邻接表/邻接矩阵+优先队列STL)
一、前言 最短路径算法,顾名思义就是求解某点到某点的最短的距离、消耗、费用等等,有各种各样的描述,在地图上看,可以说是图上一个地点到达另外一个地点的最短的距离。比方说,我们把地图上的每一个城市想象成一个点,从一个城市到另一个城市的花费是不一样的。现在我们要从上海去往北京,需要考虑的是找到一条路线,使得从上海到北京的花费最小。有人可能首先会想到,飞机直达啊,这当然是时间消耗最小的方法,但是考虑
图深度优先搜索广度优先搜索,邻接表
#include <stdafx.h>#include"iostream"#include"malloc.h"using namespace std;#define MaxVertexNum 50 //定义最大顶点数typedef struct node{ //边表结点char adjvex; //邻接点域struct node *next; //
数据结构之邻接多重表
一、特点 存储效率高:对于无向图,邻接多重表能够避免邻接表中同一条边需要存储两次的问题,因为每条边在邻接多重表中只被表示一次。 灵活性高:由于每条边同时链接在两个链表中(分别对应其两个顶点),因此在进行边的增删查改等操作时更加方便。 可读性强:邻接多重表的结构清晰,能够直观地表示无向图中顶点与边之间的关系。 二、结构 邻接多重表由顶点表和边表组成: 顶点表:存储图中的顶点信息,每个顶点元素
HDOJ 1874 畅通工程续——结构体模拟邻接链表的SPFA算法
Problem Description 某省自从实行了很多年的畅通工程计划后,终于修建了很多路。不过路多了也不好,每次要从一个城镇到另一个城镇时,都有许多种道路方案可以选择,而某些方案要比另一些方案行走的距离要短很多。这让行人很困扰。 现在,已知起点和终点,请你计算出要从起点到终点,最短需要行走多少距离。 Input 本题目包含多组数据,请处理到文
关于邻接表和其深度优先遍历、广度优先遍历的问题
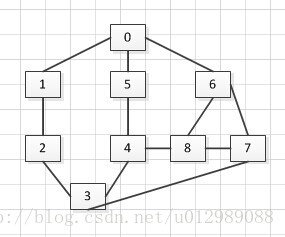
如果有一个邻接表存储的图,以0点出发,深度优先遍历和广度优先遍历。 邻接表为: [0]->[1]->[5]->[6]->END [1]->[0]->[2]->END [2]->[1]->[3]->END [3]->[2]->[4]->[7]->END [4]->[3]->[5]->[8]->END [5]->[4]->[0]->[END [6]->[0]->[8]->[7]-
【数据结构与算法】图的存储(邻接矩阵,邻接表)详解
图的邻接矩阵数据结构 typedef enum { NDG, DG, NDN, DN } GraphKind;using VRType = int;using InfoType = int;typedef struct ArcCell {VRType adj;InfoType *info;} Arc[N][N];struct MGraph {ElemType vexs[N];Arc arc;
算法竞赛入门经典邻接表
算法竞赛入门经典P360页 讲解了一个单源最短路径 并用邻接表进行了优化,当然是针对稀疏图的 经历 当时学习这个地方的时候,怎么都想不明白,后来明白了,过了一段时间,温习的时候感觉有非常强烈的清晰感。天空一声巨响,此教程要开始了。 理解 源代码不再打上来了,函数功能就是获取每一条边,并建立一个!!!关于边的序号的邻接表!!!实际上这个邻接表保存的是每一条边的序号。相信你们已经明白
图的邻接矩阵和邻接表表示法
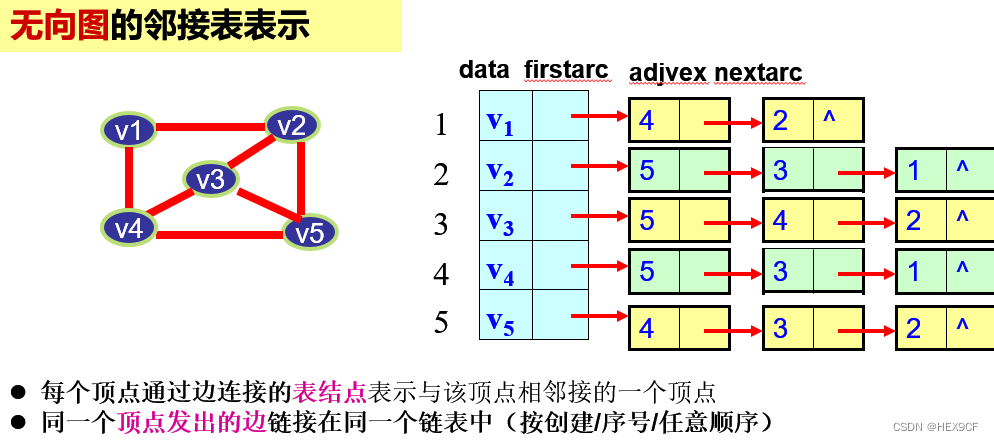
链表是一种线性存储结构,是一对一对应关系。而树是一种层次存储结构,是一对多的对应关系。而图则是一种关系存储结构,是多对多对应关系。树和图类似于数据库中的层次模型和关系模型。图的存储结构主要有两种,分别为邻接矩阵和邻接表法,其中邻接表较难,但本质相同,都是记录结点与其邻接结点,只是方法不同而已。下面分别讨论邻接表和邻接矩阵的思想。邻接表的思想是:定义三个结点,分别为表结点,头结点,邻接表结点,表结点
dijsttra 邻接表+优先队列
dijstra原理: 以单源开始,每次以新的点去更新所有的(没访问过的点) 到单源的最短路。 其中新的点---------应该找每次更新后当前到单源权值最小的点. 作法一:邻接矩阵 void DIJ(int n)//传入顶点个数n,默认0为起点 { int i,j,k; low[0]=0; bool flag[SIZE]={0}; flag[0]=1; for(i=1;
成长路上的小程序之——图的邻接表DFS、BFS
第八次数据结构上机内容:使用图的邻接表存储结构完成图的DFS、BFS遍历 本来提前就用邻接矩阵写完了,但昨晚一个贱人突然告诉我老师要求用邻接表写。。。于是加班加点,终于在今早搞出来了! 上机课的时候因为没带书,所以完全是自己敲的,期间被一个无限循环困住了!!! 在邻接链表插入新节点过程中,为p申请新空间,插入后就释放空间 在刘文斌大神的帮助下,我理解了开辟、释放空间这个概念。 我在创建图
再谈图的存储方式(邻接矩阵,邻接表,前向星)
1.邻接矩阵 1.存图思想 使用一个矩阵来描述一个图,对于矩阵的第i行第j列的值,表示编号为i的顶点到编号为j的顶点的权值。 2.代码实现 // 最大顶点数const int V = 1000;// 邻接矩阵的定义// mat[i][j] 表示 顶点'i'到顶点'j'的权值int mat[V][V];// 邻接矩阵的初始化操作// 假设权值为零表示没有该边memset(ma
POJ 1459 Power Network(Dinic邻接表+当前弧优化)
题目链接:http://poj.org/problem?id=1459 题意:一个电网包含一些结点(电站、消费者、调度站),这些结点通过电线连接。每个结点u 可能被供给s(u)的电能,s(u)≥0;同时也可能产生p(u)的电能,0≤p(u)≤pmax(u);站点u 还有可能消费c(u)电能,0≤c(u)≤min( s(u), cmax(u) );可能传输d(u)的电能,d(u) = s(u) +
数据结构-图的邻接表
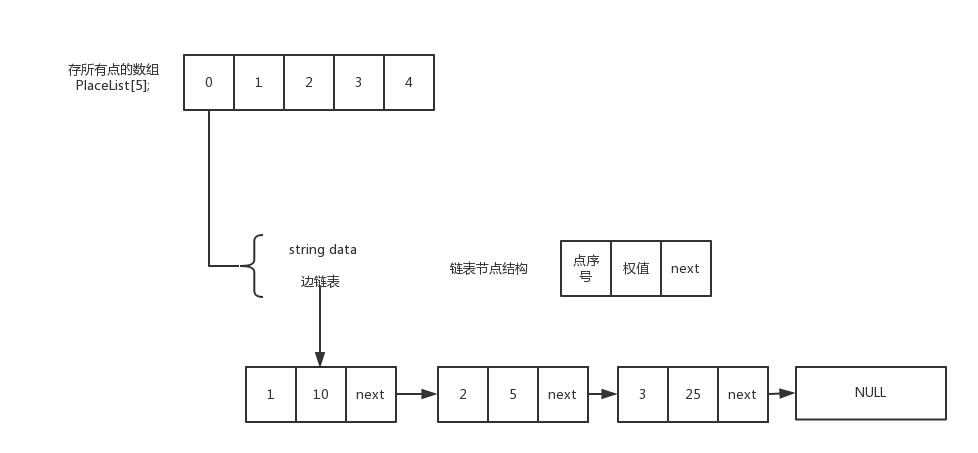
typedef struct Path //定义边表节点{int placeNum; //存储顶点下标int distance; //权重值struct Path* next; //边指针} Path;typedef struct Place /*顶点表节点*/{string data; //顶点存的数据Path* head;
数据结构——图的链表实现(邻接表表示法)
图的链表实现 之前实现了图的数组实现 http://blog.csdn.net/cinmyheart/article/details/41370465 下图仅作示意性说明,和测试数据有点区别,测试数据还是用的原来数组实现时的测试数据,这并不影响图的数据结构的表示(其实我就是懒得再做一遍原始数据了。。。哈哈) 现对图进行抽象,对于整个图,我用了结构体struct
用邻接表实现该图的广度优先搜索遍历
#include<iostream.h> const intn=8; //表示图中的最大顶点数 const inte=15; //图中的最大边数 typedefint elemtype; boolvisited[n+1]; //标志数组用于记载某个顶点是否被访问过 classlink
图的广度优先搜索(邻接表)
Problem Description 给出图的顶点数和顶点与顶点之间的连接关系,请输出用邻接表存储的图的广度优先搜索顶点序列。 Input 输入的第一行是一个整数T表示测试示例的数目,每组示例的第一行有两个数m(2<=m<=10)和n(1<=n<=m*(m-1)/2),m表示顶点的个数(顶点的标号从1-m),n表示边的个数。下面n行的每行有两个顶点号表示一条边。后面一行是一个数k,
图的深度优先搜索(邻接表)
Problem Description 给出图的顶点数和顶点与顶点之间的连接关系,请输出用邻接表存储的图的深度优先搜索顶点序列。 Input 输入的第一行是一个整数T表示测试示例的数目,每组示例的第一行有两个数m(2<=m<=10)和n(1<=n<=m*(m-1)/2),m表示顶点的个数(顶点的标号从1-m),n表示边的个数。下面n行的每行表示一条边。后面一行是一个数k,k表示需要搜
poj 2337 欧拉回路按照最小字典序输出+注意为了按最小字典序怎么处理邻接表
http://poj.org/problem?id=2337 WA了好久,昨晚1点多睡不着写的,狂WA,当时是因为用邻接矩阵存储,比如aba,aa只能存下一个,这个之前还没遇到过,今天才注意到--邻接矩阵无法存储平行边, 关于欧拉回路判断看我另几篇日志或者看我的欧拉总结 再贴个输出欧拉回路的模板 其中,参数u是起点,注意如果是输出欧拉路径的话,u必须是出度比入度大一的那个点,如果输出欧拉