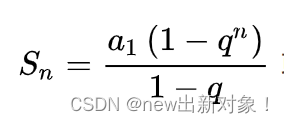逆元专题
hdu4828(卡特兰数+逆元)
这题的前几个数据分别为1,2,5,14,32......................然后确定这是个卡特兰数列 下面来介绍下卡特兰数,它的递推式为f[i+1] = f[i]*(4*n - 6)/n,其中f[2] = f[3] =1;f[4] = 2;f[5] = 14;f[6] = 32.................................. 但是这题的n太大了,所以要用到逆元,
hdu4869(逆元+求组合数)
//输入n,m,n表示翻牌的次数,m表示牌的数目,求经过n次操作后共有几种状态#include<iostream>#include<algorithm>#include<cstring>#include<stack>#include<queue>#include<set>#include<map>#include<stdio.h>#include<stdlib.h>#includ
每日一题~cf 970 div3 (A思维,B小模拟,C二分,D排列数建图成环,E 26个字母暴力+前缀和,F 逆元,G 数论gcd )
A 题意: 有 a 个1 ,b 个2.问是否能将这些数划分为两个数值相等的集合。 输出 YES 或者 NO —————— 问题等价于 将数组 分成两个数值相同的数组。所以sum 应该是偶数。也就是说 1 的个数是偶数。在i1的个数是偶数的情况下,将 2 分成两份,如果2 的个数是偶数,OK。如果是奇数那么需要1来补齐,如果1 的个数大于等于2那么可以补齐。(1 的个数是偶数,需要2个1来补齐,剩下
排列数+时间戳+逆元取模
前言:这个题目是真的难,不会做,看了题解才发现是咋回事 题目地址 最主要的就是为啥是除以3,c之前需要完成a 和 b,d 和 e 对我们的答案没有影响,所以我们要除以 A(3,3) ,但是 a 和 b 的排列没有要求,所以乘以 A( 2 , 2 ) 抵消得到 3 #include<bits/stdc++.h>using i64 = long long;using u64 =
Codeforces Round #295 (Div. 1) C. Pluses everywhere (组合数学+乘法逆元)
这题可以这样想: 对于当前第i位来说,该位若在个位上出现,那么第i位和第i+1位中间肯定有一个“+”,剩下的k-1个“+”分布在剩下的n-2个空隙中,所以出现的总次数是C(n-2,k)。同理,在十位上出现的总次数是C(n-3,k)。于是每个数字的贡献值就可以求出来了,累加即可。 所以大体思路是遍历所有可能出现的位数,从个位开始,分成两部分计算,一部分用前缀和计算出前面所
数论 —— 逆元与同余式定理
【同余模公式】 (A+B)%M = (A%M+B%M) % M(A*B)%M = (A%M*B%M) % M(A/B)%M = (A*C)%M = (A%M*C%M) % M,其中 B*C≡1(mod M),B、M 互质,C 称为 B 的逆元 (A/B)%M 的推导:(A/B)%M = (A/B) * 1 % M = (A/B)*B*C % M = (A*C) % M 【威尔逊定理】 若
同余式,乘法逆元,费马小定理
同余式 同余式是 数论 的基本概念之一,设m是给定的一个正整数,a、b是整数,若满足m| (a-b),则称a与b对模m 同余 ,记为a≡b (mod m),或记为a≡b (m)。 这个式子称为模m的同余式,若m∤ (a-b),则称a、b对模m不同余 同余概念又常表达为: 1.a=b+km (k∈Z); 2.a和b被m除时有相同的 余数 乘法逆元 乘法逆元的定义:在数学领域,对于群G
UVA 1563 - SETI (高斯消元+逆元)
UVA 1563 - SETI 题目链接 题意:根据题目那个式子,构造一个序列,能生成相应字符串 思路:根据式子能构造出n个方程,一共解n个未知量,利用高斯消元去解,中间过程有取摸过程,所以遇到除法的时候要使用逆元去搞 代码: #include <cstdio>#include <cstring>#include <algorithm>using namespace
HDU 3049 Data Processing(a/b mod c, 逆元)
题目:LINK 题目求 P = (2^(n1) + 2^(n2) + ...+ 2^(nk))/n (mod n) 对于分子部分我们可以打表求得(ps:用快速幂多次计算会TLE), 问题成了a/n mod n, 我们可以用下面解法求得。 1), a/b mod c ==> (a mod bc) / b 对于所有的情况都适用,要注意的问题就是 (b*c)*(b*c) 会不会溢出,这儿的
nyoj-Color the necklace(Ploya定理 + 欧拉函数 + 扩展欧几里得(求逆元))
题目链接:http://acm.nyist.net/JudgeOnline/problem.php?pid=688 此题题解 不太懂,因为对这些概念,定理太模糊,理解起来比较困难,不过想想还是应该把代码写出来; 题意:给你一个数 n ,代表 n 种颜色和n个珠子,问你可以组合多少种长度为n的项链;不需要用掉n种颜色,项链的旋转和翻转都是为同一条 题解: http://pan.baidu
【数学】乘法逆元进阶
乘法逆元基础 可以使用扩展欧几里得算法或费马小定理求得。 乘法逆元进阶 有一种乘法逆元的线性递推算法: 显然 1 − 1 ≡ 1 ( m o d m ) 1^{-1} \equiv 1 \pmod m 1−1≡1(modm); 对于 i − 1 i^{-1} i−1,我们令 k = ⌊ m i ⌋ k = \lfloor \frac{m}{i} \rfloor k=⌊im⌋, j =
HDU 5976 Detachment 题解(贪心+逆元+前缀和,积)
个人体会:无脑取模,最为致命!因为把存放前缀和的数组取了模,导致一些本来不等的元素变成了相同的元素,二分搜索出错。。。而且C++会T,G++就ac了。。 http://acm.hdu.edu.cn/showproblem.php?pid=5976 分解出的几个数越接近,乘积越大,如果可以相等,则分解成3的乘积,不能相等,只能分成阶乘则最大,不能分成阶乘时,把多出来的数从后往前均摊,因为如果从前往后
证明:p为质数时(p-1)!的逆元为p-1
此文章转载自:http://blog.csdn.net/YihAN_Z 证明:当p为质数时,(p-1)!的逆元为p-1。 若(p-1)!的逆元为p-1,则有 接下来证明(p-2)!与1同余。(p-2)!在模p的意义下等于1说明2~p-2可以分成若干对,每一对两两互为逆元(即每一个数乘完后可以被另一个数抵消)。由于p为质数,1~p-1的所有数都有逆元。只要证明2~p-2中的数的逆元都不等于
Modular Multiplicative Inverse(模乘逆元)
计算模乘逆元原理上有四种方法: 1.暴力算法 2.扩展欧几里得算法 3.费尔马小定理 4.欧拉定理 模乘逆元定义:满足 ab≡1(mod m),称b为a模乘逆元。以下是有关概念以及四种方法及程序。 文章出处:Modular Multiplicative Inverse The modular multiplicative inverse of an integer a modu
N-Dimensional Grid ——线性逆元
You are given an n-dimensional grid in which the dimensions of the grid are a1?×?a2?×?…?×?an. Each cell in the grid is represented as an n-tuple (x1,?x2,?…,?xn) (1?≤?xi?≤?ai). Two cells are considere
hdu 1576 A/B(求逆元模板题)
ACM国际大学生程序设计竞赛全球总决赛 A/B Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 7034 Accepted Submission(s): 5595 Problem Description 要求(A
求逆元、阶乘逆元、线性求逆元
目录 什么是逆元如何求逆元阶乘逆元线性求逆元 本文章内,若无特殊说明,数字指的是整数,除法指的是整除。 什么是逆元 我们称\(a\)是\(b\)在模\(p\)情况下的逆元,则有\(a \times b \equiv 1 ( mod\,\,p)\)。 所以呢,我们其实可以将逆元看成一个数的相反数。所以在除以一个数的时候,就相当于乘上它的相反数。 如何求逆元 我们先来看看什么情况下有逆元。
Codeforces 327C 快速幂+等比数列求和+乘法逆元
题目链接:http://codeforces.com/problemset/problem/327/C There is a long plate s containing n digits. Iahub wants to delete some digits (possibly none, but he is not allowed to delete all the digits) to f
扩展欧几里得,逆元初识(poj 1061+codeforce 7C line+hdu 1576 A/B)
poj 1061 青蛙的约会: #include <iostream>#include<cstdio>#define LL long longusing namespace std;LL gcd(LL a, LL b){return b?gcd(b,a%b):a;}void extend_Euclid(LL a,LL b,LL &x,LL &y){if(b ==
乘法逆元 hdu 1576 A/B
乘法逆元在除法取模运算中有着广泛的应用。 百度百科: 费马小定理(Fermat Theory)是数论中的一个重要定理,其内容为: 假如p是质数,且Gcd(a,p)=1,那么 a(p-1) ≡1(mod p)。即:假如a是整数,p是质数,且a,p互质(即两者只有一个公约数1),那么a的(p-1)次方除以p的余数恒等于1。 例如:a=5,p=7,满足p是质数,a,p互质的要求,因此有5^6
HDU 5698 瞬间移动 (组合数 + 阶乘逆元)
瞬间移动 Time Limit: 4000/2000 MS (Java/Others) Memory Limit: 65536/65536 K (Java/Others) Total Submission(s): 191 Accepted Submission(s): 99 Problem Description 有一个无限大的矩形,初始时你在左上角(即第一行第一列
XDU 1149 卡尔的技能 II (容斥 多重集组合 阶乘逆元)
1149: 卡尔的技能 II 时间限制: 2 Sec 内存限制: 128 MB 题目链接:http://acm.xidian.edu.cn/problem.php?id=1149 题目分析:首先这是一个多重集组合问题,请见多重集组合,所有不超过k,那就是个典型的容斥问题了,先求出总的情况数C(n + m - 1, m),然后用总的减去有至少1种元素超过k次加上至少有2种元素超过