贝尔曼专题
强化学习深入学习(一):价值函数和贝尔曼方程
文章目录 0. 引言1. 回报(Return)2. 价值函数(Value Function)3. 贝尔曼期望方程(Bellman Expectation Equation)4. 贝尔曼最优方程(Bellman Optimality Equation)总结 0. 引言 强化学习(Reinforcement Learning, RL)是一种机器学习方法,通过与环境的交互来学习如何
HDU 2544 最短路——贝尔曼福特(结构体优化) spfa算法
最短路 Time Limit: 5000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 29251 Accepted Submission(s): 12644 Problem Description 在每年的校赛里,所有进入决赛的同学都会
POJ 1860Currency Exchange(贝尔曼最短路)
题目地址:http://poj.org/problem?id=1860 这个题一道很简单的贝尔曼判环的应用,用贝尔曼判环挺方便的。因为把r,c定义成了整型,错了一晚上。。。 #include <iostream>#include <stdio.h>#include <string.h>#include <stdlib.h>#include <math.h>#include <ct
POJ 3259Wormholes(贝尔曼最短路)
题目地址:http://poj.org/problem?id=3259 由于spfa是贝尔曼算法的队列优化,于是贝尔曼算法被我完全忽视了。。现在才发现贝尔曼算法在判断负环方面还是挺有用的。。 #include <iostream>#include <stdio.h>#include <string.h>#include <stdlib.h>#include <math.h>#in
⭐ ▶《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch3 贝尔曼最优公式 【压缩映射定理】
PPT 截取必要信息。 课程网站做习题。总体 MOOC 过一遍 1、视频 + 学堂在线 习题 2、过 电子书,补充 【下载:本章 PDF 电子书 GitHub 界面链接】 [又看了一遍视频] 3、总体 MOOC 过一遍 习题 学堂在线 课程页面链接 中国大学MOOC 课程页面链接 B 站 视频链接 PPT和书籍下载网址: 【GitHub 链接】 强化学习的最终目标: 寻求最优策略
▶《强化学习的数学原理》(2024春)_西湖大学赵世钰 Ch2 贝尔曼公式
PPT 截取有用信息。 课程网站做习题。总体 MOOC 过一遍 1、学堂在线 视频 + 习题 2、相应章节 过电子书 复习 GitHub界面链接 3、总体 MOOC 过一遍 学堂在线 课程页面链接 中国大学MOOC 课程页面链接 B 站 视频链接 PPT和书籍下载网址: 【github链接】 onedrive链接: 【书】 【课程PPT】 文章目录 计算 return方法一:
【TensorFlow深度学习】强化学习中的贝尔曼方程及其应用
强化学习中的贝尔曼方程及其应用 强化学习中的贝尔曼方程及其应用:理解与实战演练贝尔曼方程简介应用场景代码实例:使用Python实现贝尔曼方程求解状态价值结语 强化学习中的贝尔曼方程及其应用:理解与实战演练 在强化学习这一复杂而迷人的领域中,贝尔曼方程(Bellman Equation)扮演着核心角色,它是连接过去与未来、理论与实践的桥梁,为智能体的决策优化提供了数学基础。本
大模型微调实战之强化学习 贝尔曼方程及价值函数(一)
大模型微调实战之强化学习 贝尔曼方程及价值函数 强化学习(RL)是机器学习中一个话题,不仅在人工智能方面。它解决问题的方式与人类类似,我们每天都在学习并在生活中变得更好。 作为一名大模型学习者,当开始深入研究强化学习时,需花了一些时间来了解幕后发生的事情,因为它与传统的机器学习技术相比往往有所不同。这篇文章将帮助你了解 强化学习算法的组成部分以及如何利用它们来解决 RL 问题。 强化学习问题
大模型微调实战之强化学习 贝尔曼方程及价值函数(五)
大模型微调实战之强化学习 贝尔曼方程及价值函数(五) 现在, 看一下状态-动作值函数的示意图: 这个图表示假设首先采取一些行动(a)。因此,由于动作(a),代理可能会被环境转换到这些状态中的任何一个。因此,提出一个的问题:采取行动(a)有多好? 再次对两个状态的状态值进行平均,并添加立即奖励,该奖励告诉大家采取特定操作 (a) 有多好。这定义了 q π(s,a)。 从数学上来说, 可以
【强化学习的数学原理-赵世钰】课程笔记(二)贝尔曼公式
【强化学习的数学原理-赵世钰】课程笔记(二)贝尔曼公式 一. 内容概述 1. 第二章主要有两个内容 (1)一个核心概念:状态值(state value):从一个状态出发,沿着一个策略我所得到的奖励回报的平均值。状态值越高,说明对应的策略越好。之所以关注状态值,是因为它能评价一个策略的好坏。 (2)基本工具:贝尔曼公式(the Bellman equation): 用于分析状态值,描述所有
贝尔曼最优方程【BOE】
强化学习笔记 主要基于b站西湖大学赵世钰老师的【强化学习的数学原理】课程,个人觉得赵老师的课件深入浅出,很适合入门. 第一章 强化学习基本概念 第二章 贝尔曼方程 第三章 贝尔曼最优方程 文章目录 强化学习笔记一、最优策略二、贝尔曼最优方程(BOE)三、BOE的求解1 求解方法2 实例 四、BOE的最优性参考资料 上一节讲了贝尔曼方程,这一节继续在贝尔曼方程的基础上
对贝尔曼福德算法进行改进
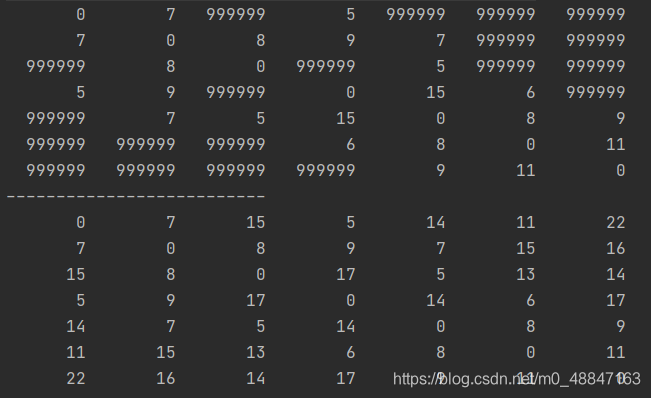
对于贝尔曼福德算法的时间复杂度是V的绝对值和E的绝对值的乘积,如果说给定的图的节点的数量和边的数量都是较大的情况的时候,算法的运行效率就会非常的低,速度也相应的很慢,所以针对这种情况,对算法进行改进,首先是给定图并将图中的每个节点进行编号: 添加图片注释,不超过 140 字(可选) 图中的节点包含数字表示节点所对应的编号,此时将图中的边进行分组,分为两组,第一组边的起点编号是小于终点编
【RL】Bellman Equation (贝尔曼等式)
Lecture2: Bellman Equation State value 考虑grid-world的单步过程: S t → A t R t + 1 , S t + 1 S_t \xrightarrow[]{A_t} R_{t + 1}, S_{t + 1} StAt Rt+1,St+1 t t t, t + 1 t + 1 t+1:时间戳 S t S_t St:时间
强化学习从基础到进阶-案例与实践[2]:马尔科夫决策、贝尔曼方程、动态规划、策略价值迭代
【强化学习原理+项目专栏】必看系列:单智能体、多智能体算法原理+项目实战、相关技巧(调参、画图等、趣味项目实现、学术应用项目实现 专栏详细介绍:【强化学习原理+项目专栏】必看系列:单智能体、多智能体算法原理+项目实战、相关技巧(调参、画图等、趣味项目实现、学术应用项目实现 对于深度强化学习这块规划为: 基础单智能算法教学(gym环境为主)主流多智能算法教学(gym环境为主) 主流算法:D
深入理解强化学习——马尔可夫决策过程:策略迭代-[贝尔曼最优方程]
分类目录:《深入理解强化学习》总目录 当我们一直采取 arg max \arg\max argmax操作的时候,我们会得到一个单调的递增。通过采取这种贪心 arg max \arg\max argmax操作,我们就会得到更好的或者不变的策略,而不会使价值函数变差。所以当改进停止后,我们就会得到一个最佳策略。当改进停止后,我们取让Q函数值最大化的动作,Q函数就会直接变成价值函数
图的搜索(二):贝尔曼-福特算法、狄克斯特拉算法和A*算法
图的搜索(二):贝尔曼-福特算法、狄克斯特拉算法和A*算法 贝尔曼-福特算法 贝尔曼-福特(Bellman-Ford)算法是一种在图中求解最短路径问题的算法。最短路径问题就是在加权图指定了起点和终点的前提下,寻找从起点到终点的路径中权重总和最小的那条路径。 设置A为起点,G为终点。 首先设置各个顶点的初始权重 :起点为 0,其他顶点为无穷大(∞)。这个权重表示的是从 A 到该顶点的
强化学习-赵世钰(二):贝尔曼公式/Bellman Equation【用于计算State Value:①线性方程组法、②迭代法】、Action Value【据状态值求解得到;用来评价action优劣】
State Value :the average Return that an agent can obtain if it follows a given policy/π【给定一个policy/π,所有可能的trajectorys得到的所有return的平均值/期望值: v π ( s ) ≐ E [ G t ∣ S t = s ] v_\pi(s)\doteq\mathbb{E}[G_t|
关于求图的最短路径的算法:普利姆算法,迪鲁斯卡尔算法,弗洛伊德算法,贝尔曼福特算法!!!
本篇用于记录我在做图的最短路径的问题过程中学到的算法,如果有不足之处,还请指出。 关于图的最短路径,有四种算法,分别是普利姆算法,迪鲁斯卡尔算法,弗洛伊德算法和贝尔曼福特算法,接下来将对这些算法依次进行讲解。 1.普利姆算法 普里姆算法(Prim算法),是图论中的一种算法,可在加权连通图里搜索最小生成树,也就是求最小权值,最后生成的路径(也就是两个点之间的路径个数)个数比点少一,比如下面的图
【算法-动态规划】贝尔曼福特算法
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kuan 的首页,持续学习,不断总结,共同进步,活到老学到老导航 檀越剑指大厂系列:全面总结 java 核心技术点,如集合,jvm,并发编程 redis,kafka,Spring,微服务,Netty 等常用开发工具系列:罗列
泛函分析(二)巴纳赫(Banach)不动点,贝尔曼方程(Bellman equation)在强化学习的应用
前言 强化学习的目的是寻找最优策略。其中涉及两个核心概念最优状态值和最优策略,以及贝尔曼最优公式。而贝尔曼最优公式用不动点原理求解地址,由Banach不动点定理可以知道,强化学习一定存在唯一的解(策略) ,并且可以通过迭代求得。 1.贝尔曼方程 贝尔曼方程在强化学习(RL)中无处不在,由美国应用数学家理查德·贝尔曼(Richard Bellman)提










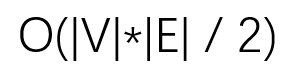

![强化学习从基础到进阶-案例与实践[2]:马尔科夫决策、贝尔曼方程、动态规划、策略价值迭代](https://ai-studio-static-online.cdn.bcebos.com/22ecbc23fdc340bfbf3a60e94532af69bf39ec80c35e497484eeb8e2a5bfa5a3)