本文主要是介绍对贝尔曼福德算法进行改进,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
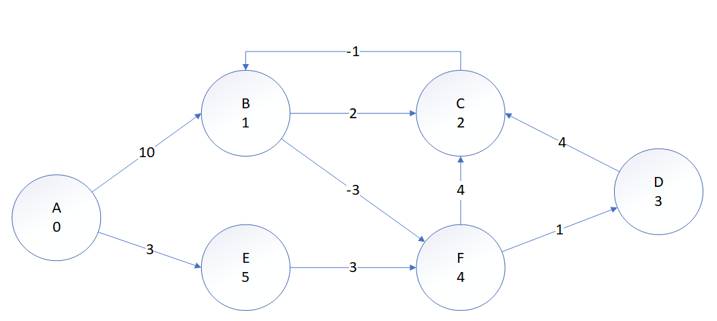
对于贝尔曼福德算法的时间复杂度是V的绝对值和E的绝对值的乘积,如果说给定的图的节点的数量和边的数量都是较大的情况的时候,算法的运行效率就会非常的低,速度也相应的很慢,所以针对这种情况,对算法进行改进,首先是给定图并将图中的每个节点进行编号:
添加图片注释,不超过 140 字(可选)
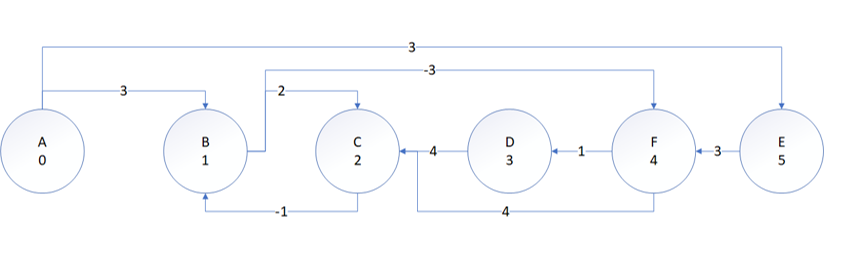
图中的节点包含数字表示节点所对应的编号,此时将图中的边进行分组,分为两组,第一组边的起点编号是小于终点编号的,第二组边的起点编号是大于终点编号的,(A,B)(A,E)(B,C)(B,F)以及(C,B)(D,C)(F,D)(F,C)(E,F)两组。然后将图中节点编号次序排列成一行,将第一组绘制在上方,第二组边绘制在中间或者下方,如下图所示:
添加图片注释,不超过 140 字(可选)
如果在内层循环遍历边的时候,现按照节点编号从小到大遍历上方路径,再根据节点编号从大到小便利中间路径或者下方路径,可以将这个性质扩展到所有的图形当中去,对给定任意图形,将起始节点编号为0,其他点可以任意编号,那么就可以像上图一样改造编号后的图,假设起始节点s到给定节点v的最短路径为s=v0,...vn=v。
考虑相邻两条边出现反转的情况,也就是上一条边位于改造后图的上方,下一条边位于改造后图的中间或者下方,或者是上一条边位于改造后的图的中间或者下方,下一条边位于改造后图的上方。
如果最短路径中不存在这种反转,那么依照节点的编号从小到大遍历一次上方的边,然后在依照编号从大到小遍历中间或者下方的边,一次遍历之后就能得到起始节点与给定节点的最短路径。
最后就是算法的时间复杂度为:
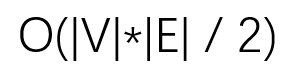
添加图片注释,不超过 140 字(可选)
相对于原来的说,效率就改进了一倍的情况。
这篇关于对贝尔曼福德算法进行改进的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!





