关于求图的最短路径的算法：普利姆算法，迪鲁斯卡尔算法，弗洛伊德算法，贝尔曼福特算法！！！

本篇用于记录我在做图的最短路径的问题过程中学到的算法，如果有不足之处，还请指出。

关于图的最短路径，有四种算法，分别是普利姆算法，迪鲁斯卡尔算法，弗洛伊德算法和贝尔曼福特算法，接下来将对这些算法依次进行讲解。

1.普利姆算法

普里姆算法（Prim算法），是图论中的一种算法，可在加权连通图里搜索最小生成树，也就是求最小权值，最后生成的路径（也就是两个点之间的路径个数）个数比点少一，比如下面的图是7个点，那么生成的边就是6个。

就随便拿一个图来讲解。普利姆算法首先有两个集合，一个是已经遍历过的集合，一个是没有遍历过的集合，每回从第一个集合中拿出一个点与第二个集合中的点进行判断，找出拥有最小路径的点，然后将最小路径的两个点中没有在第一个集合中的点加入到第一个集合中。下面是代码：

public class PrimAlgorithm {public static void main(String[] args) {int[][] graph = {{0,7,0,5,0,0,0},{7,0,8,9,7,0,0},{0,8,0,0,5,0,0},{5,9,0,0,15,6,0},{0,7,5,15,0,8,9},{0,0,0,6,8,0,11},{0,0,0,0,9,11,0}};char[] charset = {'A','B','C','D','E','F','G'};boolean[] visited = new boolean[charset.length];MyGraph mg = new MyGraph(graph,charset,visited);mg.getMinbornTree(2);}
}class MyGraph{private int[][] adj;//邻接图，用来存储节点之间的权值private char[] charset;//字符集，为了输出明确boolean[] isVisited ;//用来标记指定的点是否访问过public MyGraph() {}//初始化public MyGraph(int[][] adj,char[] charset,boolean[] isVisited) {this.adj = adj;this.charset = charset;this.isVisited = isVisited;}public void getMinbornTree(int index){//如果图为空就不用遍历了if(adj.length != 0) {isVisited[index] = true;getMinbornTree();}else{System.out.println("图为空");}}private void getMinbornTree(){for(int k = 1; k < adj.length; k++){//h1，h2指向这一次遍历拥有最小距离的两个点int h1 = -1, h2 = -1;int min = 9999999;for(int i = 0; i < adj.length;i++){if(isVisited[i]){continue;}for(int j = 0; j < adj.length; j++){if(isVisited[i] && !isVisited[j] && adj[i][j] != 0 && adj[i][j] < min){h1 = i;h2 = j;min = adj[i][j];}}}isVisited[h2] = true;System.out.println("从"+charset[h1]+"->"+charset[h2]+"权值为:"+min);}}
}

有什么问题大家可以指出来，这只是一种思路，具体的实现要看个人怎么写。

2.迪鲁斯卡尔算法

克鲁斯卡尔算法和普利姆算法一样，也是求最小生成树的算法。不过普利姆算法是以任意一个点开始求最小生成树，克鲁斯卡尔算法是以边的权值为准开始求最小生成树（也就是按权值从小到大求最小生成树），在搜索的过程中，还要注意不能选取两个已经选过的点，这样会构成一条回路，不符合最小生成树。
下面是代码：

import java.util.*;public class DyruskalAlgorithm {static int[] pre;public static void main(String[] args) {Scanner sc = new Scanner(System.in);int length = sc.nextInt();//初始化图int[][] nums = new int[length][length];//这个图中存在多少边int m = sc.nextInt();//nodes存储边及其两个顶点Node[] nodes = new Node[m];for (int i = 0; i < m; i++) {nodes[i] = new Node();}//用来存储每个点的祖先pre = new int[length];//起初的时候每个点的祖先是它们自己for (int i = 0; i < length; i++) {pre[i] = i;}int index = 0;while(m != 0){int x = sc.nextInt(), y = sc.nextInt(),weight = sc.nextInt();nums[x-1][y-1] = weight;nodes[index].start = x-1;nodes[index].end = y-1;nodes[index].weight = weight;index++;m--;}//将这些边进行排序，权值小的放在前面，权值大的放在后面Arrays.sort(nodes);dyruskal(nums,nodes);}public static void dyruskal(int[][] map,Node[] nodes){for(int k = 1; k < map.length; k++){for(int i = 0; i < nodes.length; i++){//由于是找最小的权值，一旦满足条件就可以直接跳出这一层循环if(find(nodes[i].start) != find(nodes[i].end)){System.out.println("从"+(nodes[i].start+1)+"到"+(nodes[i].end+1)+"权值为："+nodes[i].weight);pre[nodes[i].end] = pre[nodes[i].start];break;}}}}//这里要用到公共祖先，也就是union-find（并查集）算法、不熟悉的可以看一下，不然会有点看不懂public static int find(int x){while(x != pre[x]){x = pre[x];}return x;}
}//存储边的信息
class Node implements Comparable<Node>{int start;int end;int weight;public Node() {}public Node(int start, int end, int weight) {this.start = start;this.end = end;this.weight = weight;}//实现Compareable对权值进行排序@Overridepublic int compareTo(Node o) {return this.weight-o.weight;}
}

3.弗洛伊德算法

弗洛伊德算法是用来求任意两个节点之间最小距离的一种算法，与Dijkstra算法类似。该算法是一种在具有正或负边缘权重（但没有负环）的加权图中找到最短路径的算法，即支持负权值但不支持负权环。简单点说就是A,B,C三个点如果A->B+B->C之间的距离小于A->B之间的距离，那么A->B的最小距离就变成A->B+B->C了。很明显，想要确定任意两个点之间的距离，就还需要一个点来作为中间节点来完成这个操作。简单说明了一下，那么接下来就是代码部分：

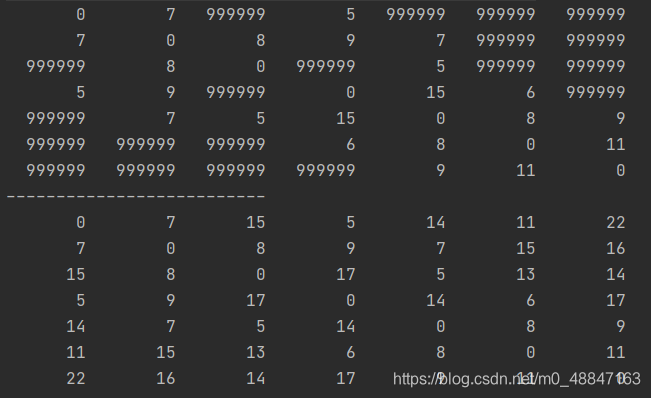
public class Floyd {public static void main(String[] args) {int max = 999999;//存储原来图中的各个节点之间的距离，自己与自己的距离为0，达不到的边为max//图你也可以自己进行输入，并不一定要固定成静态的int[][] map = {{0,7,max,5,max,max,max},{7,0,8,9,7,max,max},{max,8,0,max,5,max,max},{5,9,max,0,15,6,max},{max,7,5,15,0,8,9},{max,max,max,6,8,0,11},{max,max,max,max,9,11,0}};//使用算法前for (int i = 0; i < map.length; i++) {for (int j = 0; j < map[i].length; j++) {System.out.printf("%8d ",map[i][j]);}System.out.println();}//算法过程for(int k = 0; k < map.length; k++){//中间节点for(int i = 0; i <map.length; i++){//起始节点for(int j = 0; j < map.length; j++){//终点节点if(map[i][k]+map[k][j] < map[i][j]){map[i][j] = map[i][k]+map[k][j];//这里还可以加别的，比如路径啥的可以自己实现。}}}}//使用算法后的距离System.out.println("--------------------------");for (int i = 0; i < map.length; i++) {for (int j = 0; j < map[i].length; j++) {System.out.printf("%8d ",map[i][j]);}System.out.println();}}
}

运算结果：（如果不对，可以指出来）

4.贝尔曼福特算法

第一次遇到这种算法是我在做练习的时候，使用我已知的算法来求解求解不出来，后来参考答案之后，才大概理解了。下面讲的可能不是太清楚，各位别太在意。
贝尔曼-福特算法（Bellman-Ford）是由理查德.贝尔曼和 莱斯特·福特 创立的，是求解单源最短路径的一种算法，意思就是求一个点到任意节点之间的距离。它和上面的弗洛伊德算法有点相似，但是又有不同之处。贝尔曼-福特算法以松弛操作为基础，即估计的最短路径值渐渐地被更加准确的值替代，直至得到最优解（这里的最优解代码中会添加注释）。下面先附上代码：

import java.util.Arrays;
import java.util.Scanner;public class Bellman_Ford {//给定一个n个顶点，m条边的有向图（其中某些边权可能为负，但保证没有负环）。请你计算从任意节点到其他点的最短路（顶点从1到n编号）。static int[] I;//边的起始点static int[] J;//边的终点static int[] W;//边的权值static int[] before;//记录这个点到其他点的距离的前一个状态static int[] dis;//当前点到其他点的距离//这里文章中写道的“直到得到最优解”就是判断dis和before的状态是否相同，如果相同则表示到了最优解，不用再进行松弛操作public static void main(String[] args) {Scanner sc = new Scanner(System.in);int n = sc.nextInt(), m = sc.nextInt();I = new int[m + 1];J = new int[m + 1];W = new int[m + 1];before = new int[n + 1];dis = new int[n + 1];for (int i = 1; i <= m; i++) {I[i] = sc.nextInt();J[i] = sc.nextInt();W[i] = sc.nextInt();}bellman_ford(1);for (int i = 1; i < dis.length; i++) {System.out.print(dis[i] + " ");}}//index下标从1开始public static void bellman_ford(int index) {Arrays.fill(dis, 999999);dis[index] = 0;//表示自己到自己的距离为0for (int i = 1; i < before.length; i++) {//这里要对dis进行松弛，所以将前一个状态赋给beforefor (int j = 1; j < before.length; j++) {before[j] = dis[j];}for (int j = 1; j < I.length; j++) {if (dis[J[j]] > dis[I[j]] + W[j]) {//如果index 到 J[j]的距离比index到I[j]加上I[j]到J[j]的距离大，则进行变化dis[J[j]] = dis[I[j]] + W[j];}}boolean flag = true;for (int j = 1; j < dis.length; j++) {if (dis[j] != before[j]) {flag = false;break;}}if (!flag) {break;}}}
}

这大概就是贝尔曼福特算法，最后希望对各位有所帮助，有不足之处希望各位可以指出来。。。