本文主要是介绍03 贝尔曼公式,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
贝尔曼公式
- 前言
- 1、Motivating examples
- 2、state value
- 3、Bellman equation:Derivation
- 4、Bellman equation:Matrix-vector form
- 4、Bellman equation:Solve the state value
- 5、Action value
前言
本文来自西湖大学赵世钰老师的B站视频。本节课主要介绍贝尔曼公式。
本节课概要:本节课需要抓住两个内容,state value 和 the Bellman equation。本次大纲如下:

1、Motivating examples

return就是有多条轨迹,沿着这些轨迹可以得到很多的rewards,把这些rewards求和,就得到return。为什么return这么重要呢?通过上图三个例子来做介绍,上面三幅图的环境是一样的,s4是目标,s2是forbidden area,白色的是accessible area。这三幅图不同的是在状态s1上的策略是不同的,第一幅图在s1会往下走,第二幅图在s1会往右走,第三幅图在s1有50%的概率往下走,50%的概率往右走,在其他位置上,它们的策略是一样的。
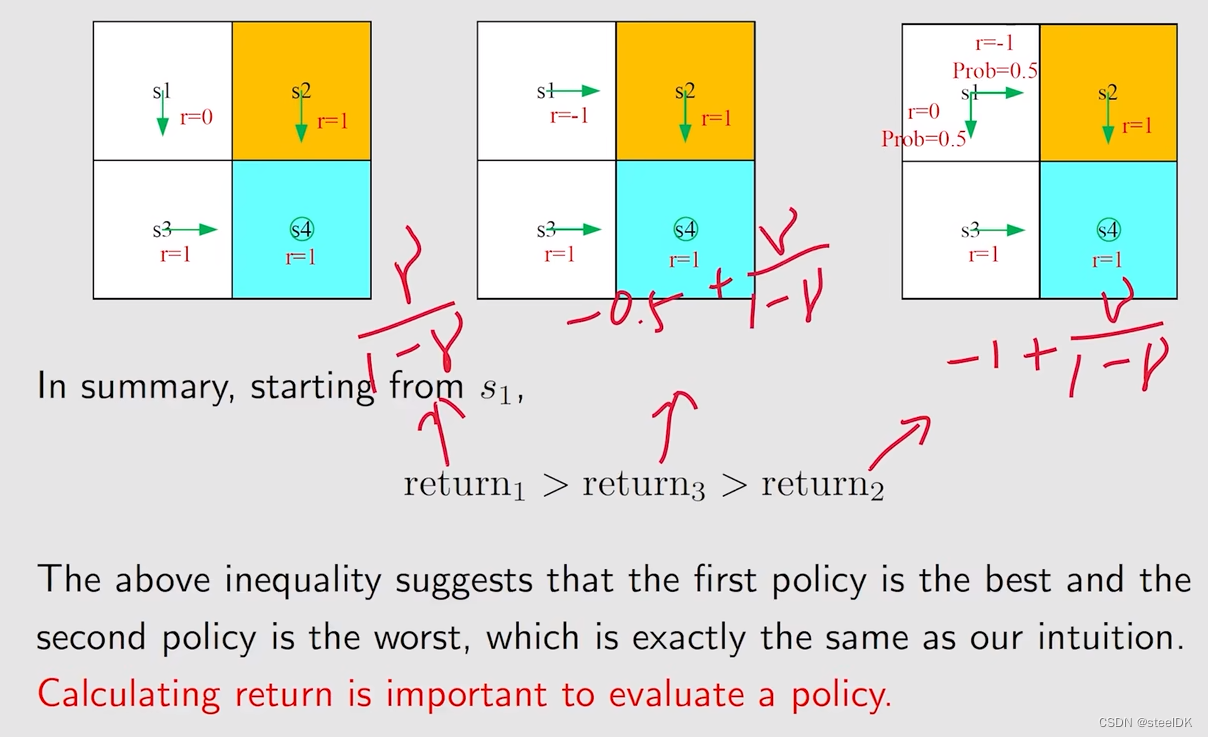
因此,我们需要回答,从s1出发,哪一个策略是最好的,哪一个策略是最差的,从直观上来说,第一幅图的策略是最好的,第二幅图的策略是最差的,第三幅图的策略不好也不差。因为第一幅图从s1出发不会进入到forbidden area,第二幅图会直接进入forbidden area,第三幅图有50%的概率进入到forbidden area。那么我们可以用数学来描述这一种直观,数学工具就是这个return。return之所以重要,是因为它告诉我们哪个策略好,哪个策略坏,即它能够评估策略。
下面我们分别来计算这三个例子对应的return:
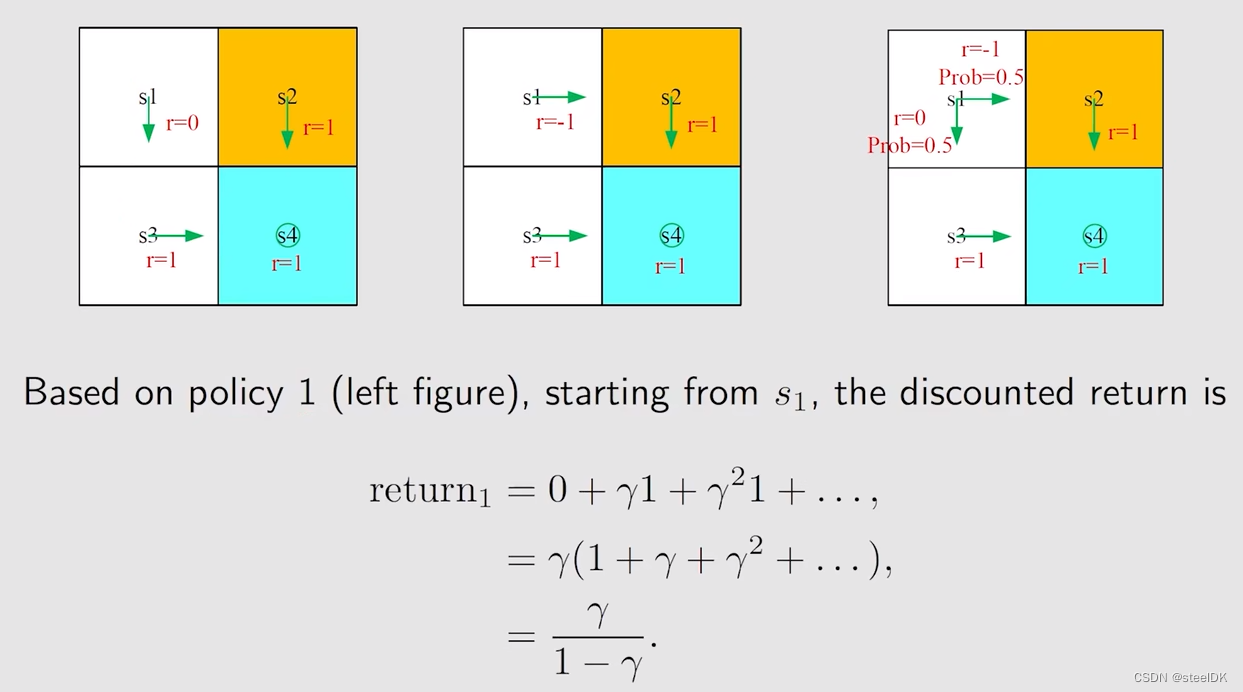
对于第一幅图,从s1到s3,得到的reward为0,从s3到s4得到的reward为γ乘以1,然后就会一直呆在s4,得到的结果如上图。同样的方法我们可以得到第二幅图和第三幅图对应的return。策略3对应的return实际上就是我们接下来要学的state value。


下面做个总结:
下面进一步来讲一下return如何计算。
考虑从不同状态出发,计算的return。用vi表示从状态si出发得到的return。有两种方法,第一种方法为:

第二种方法为:

v1就是从s1出发,到达s2之后,就相当于从s2出发了,从s2出发一定得到的是v2,因此v1可以写成上述形式,依次类推。
但同样也面临着一些问题,在计算时我们要求解v,但还得事先知道v,这个好像陷入了一个不可能解决的问题。看似好像无法解决,但如果我们用数学的话,就可以解决了,首先我们将上图中的式子写成矩阵和向量的形式:
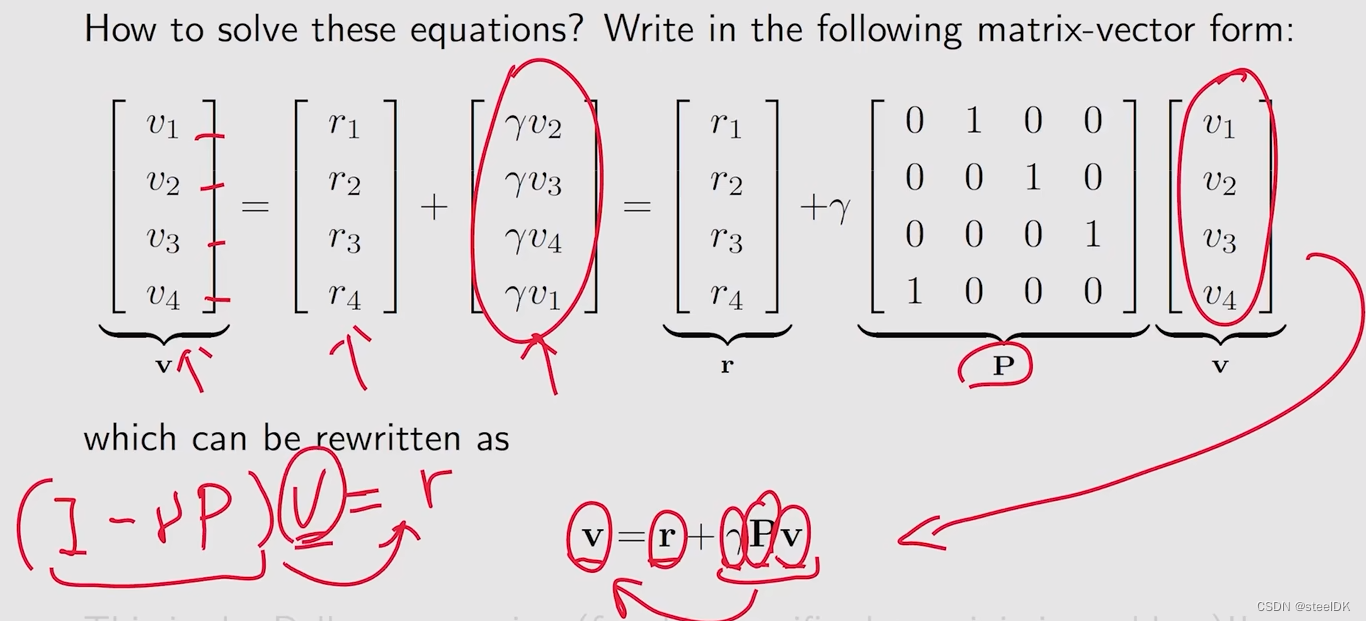

这是一个比较简单的,特别是针对确定性问题的贝尔曼公式,后面会更加正式地介绍一般化地贝尔曼公式。但这个公式也告诉我们,一个状态地value实际上依赖于其他状态地value,这个就是bootstrapping想法;另外就是matrix-vector form也是非常重要地,就是我们只看一个公式是没办法解决的,但我们把所有的公式全都组合到一起,得到一个matrix-vector form就很容易求出来。
下面我们在做一个例子来加深理解:

2、state value
这一部分介绍state value概念。为了介绍state value,我们首先引入一些符号:

首先看单步的,St是当前状态,在当前状态下采取的动作是At,得到的下一个reward是Rt+1,跳到下一个状态是St+1。t指的是当前时刻,t+1指的是下一时刻。

St、At、Rt+1都是随机变量,这也就意味着我们可以求解它们的期望。这样单步的过程可以推广到多步的trajectory。下图中的Gt也是一个随机变量。

有了以上基础,我们可以来定义state value了:
第一点:state value function 是关于状态s的函数,从不同的s出发,得到的轨迹不同,显然得到的discount return也不同,求平均也是不同的;第二点:state value function是一个策略的函数,显然不同的策略会得到不同的轨迹,不同的轨迹又会得到不同的return,进而会得到不同的state value。最后一点是,这个state value不仅仅是一个数值的value,它也代表一种价值,当一个state value比较大的时候,就代表这个状态是比较有价值的,因为从这个状态出发,我们会得到更多的return。
最后来回答这样一个问题:state value和return有什么区别?return是针对单个trajectory求的return,而state value是对多个trajectory得到的return再求平均值,如果我们从一个状态出发,有可能得到多个trajectory,此时return和state value是有区别的,但是如果我们从一个状态出发,一切都是确定性的,也就是说只能得到一条trajectory,此时从那个状态出发得到的return和state value是一样的。
下面我们来看一个例子:

上述三幅图分别对应三个策略,假设从左到右分别是π1、π2、π3,接下来我们计算在这三个不同策略下,同一个状态s1的state value。计算vπ1(s1)、vπ2(s1)、vπ3(s1)可知,第一幅图对应的策略是最好的。(上图所举例子是求确定性的trajectory下的state value)
3、Bellman equation:Derivation
我们首先来学习的是如何来推到贝尔曼公式。本小节重点如下:

总结:我们要学会用贝尔曼公式计算上节中提到的state value,贝尔曼公式用一句话可以概况来说就是它描述了不同状态的state value之间的关系。

首先考虑这样一个trajectory,从状态St出发,采取动作At,得到Rt+1和St+1,以此类推,得到了上图中的一个trajectory。这样的一个trajectory可以计算它的discounted return Gt,从上图推导后的公式来看,Gt就等于我立刻能得到的immediate reward Rt+1,再加上从下一时刻出发得到的Gt+1乘以discount rate γ。

从上图可以看出,state value可以用蓝色的两个期望来表示,分别计算这两个期望就能得到贝尔曼公式。下图就是第一个期望的计算方法:

第一项期望实际上就是immediate rewards的mean,第二项的期望公式见下图:

第二项是从当前状态s出发所得到的下一时刻的return的mean。从当前状态出发,可以有多个选择,可以跳到s撇,跳到不同s撇的概率是p(s撇|s),跳到s撇得到的期望值是E(Gt+1|St=s,St+1=s撇),E(Gt+1|St=s,St+1=s撇)指的是当前状态是s,下一时刻状态是s撇,计算从下一个状态出发,所得到的return的mean。E(Gt+1|St=s,St+1=s撇)中的St=s是可以去掉的,因为我已经知道了下一个状态是s撇,就不用关心之前是什么状态了。E(Gt+1|St+1=s撇)就是针对s撇的state value,用vπ(s撇)。从s到s撇的概率p(s撇|s)就是从状态s出发,选取不同的动作a的概率,乘以当前状态下采取动作a得到s撇的概率,不同动作a求和就是p(s撇|s)。
总之,第二个期望就是未来rewards的一个均值。
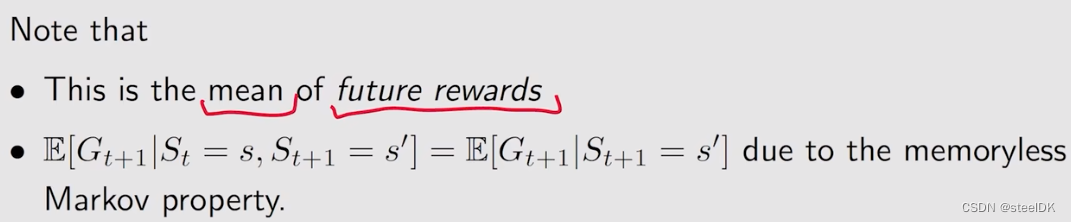
至此,我们就可以给出贝尔曼公式的表达式了:

上图中的公式就是贝尔曼公式,它实际上描述了不同状态的state value之间的关系。公式左边是s的state value,右边是s撇的state value。另外,这个式子包含两项,一项是immediate reward,另一项是future reward。上述式子应该是对状态空间中所有的状态都成立的,所以,如果我们有n个状态,我们就会有n个这样的式子,通过n个这样的式子,我们就可以把state value给求解出来,但我们通常就写上述一个式子,大家千万不要以为贝尔曼公式就只有这一个式子。

状态值如何计算呢?vπ(s)依赖于vπ(s撇),而vπ(s撇)又依赖于其它状态值,看起来似乎没办法计算,这其实就是bootstrapping,我们可以用矩阵来进行计算。另外,这个式子依赖于很多概率,π(a|s)是policy,贝尔曼公式是依赖于概率的,我们要把state value给计算出来,实际上我们现在正在做的事情就叫policy evaluation,就是去evaluation这个policy是好是坏。

上图中的绿色箭头就是策略π。

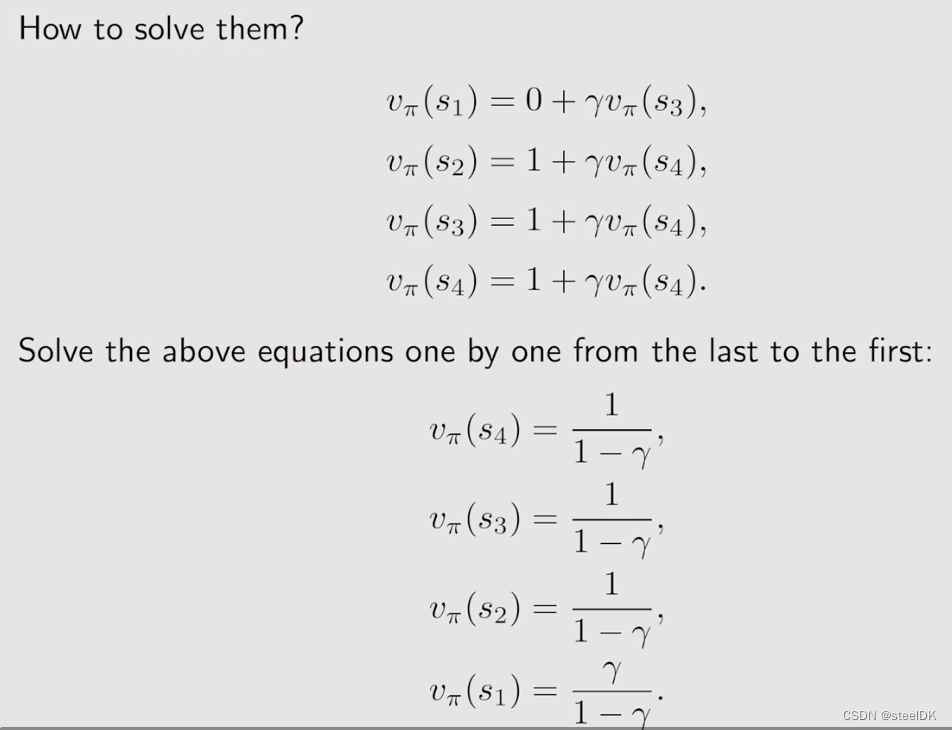

如果假设γ=0.9,得到的结果见上图。state value实际上是代表了他的价值,如果一个状态价值高,说明了这个状态是值得我们往那个方向走的,在上图中,为什么s2,s3,s4的价值高呢,是因为他们离target area是比较近的,而s1离得较远。计算得到这个状态值之后,我们就可以去改进这个策略,慢慢的我们就可以得到最优的策略。
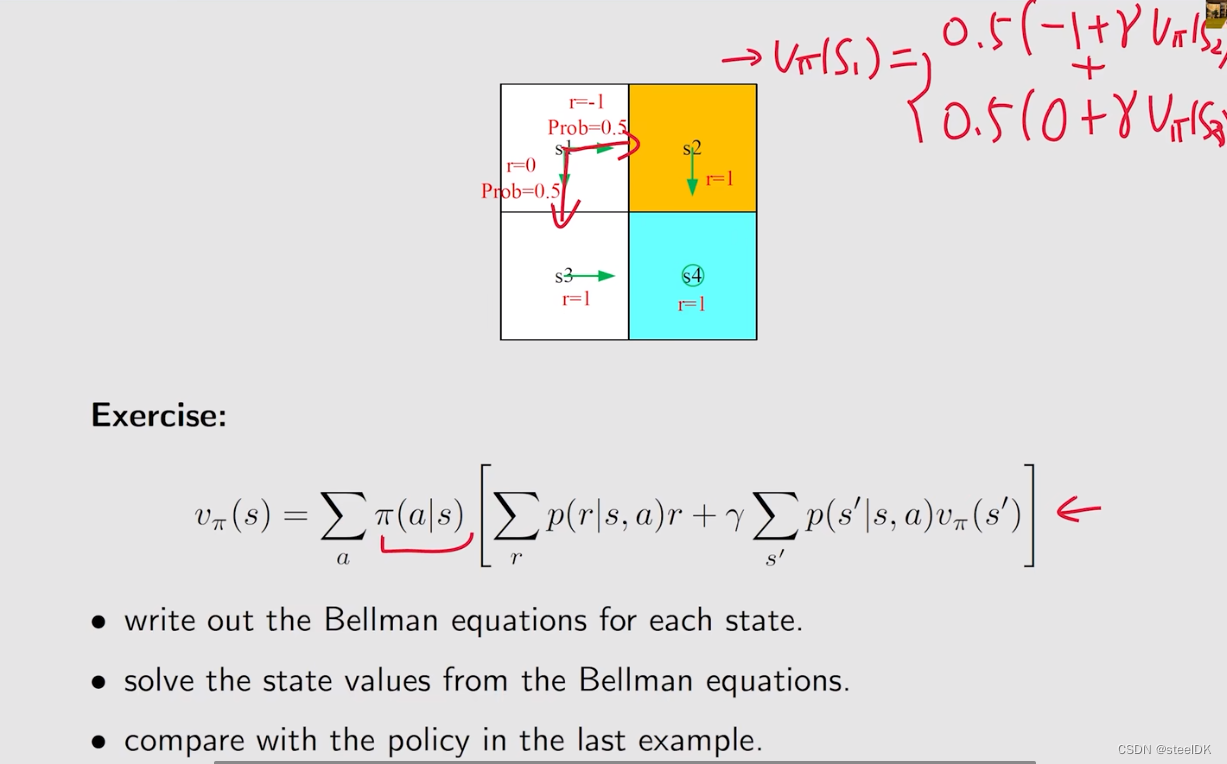

4、Bellman equation:Matrix-vector form
在上节中,我们介绍了贝尔曼公式的推导,这节来介绍贝尔曼公式的矩阵和向量形式。

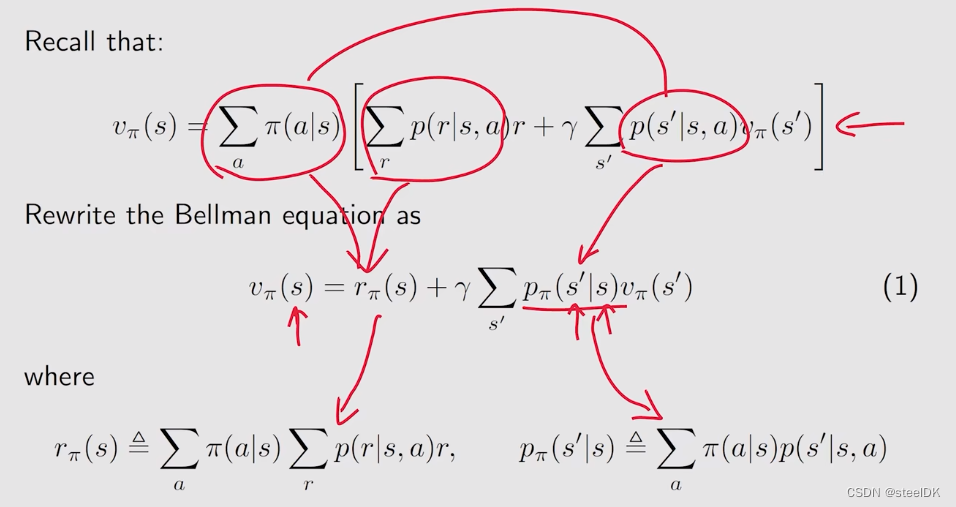
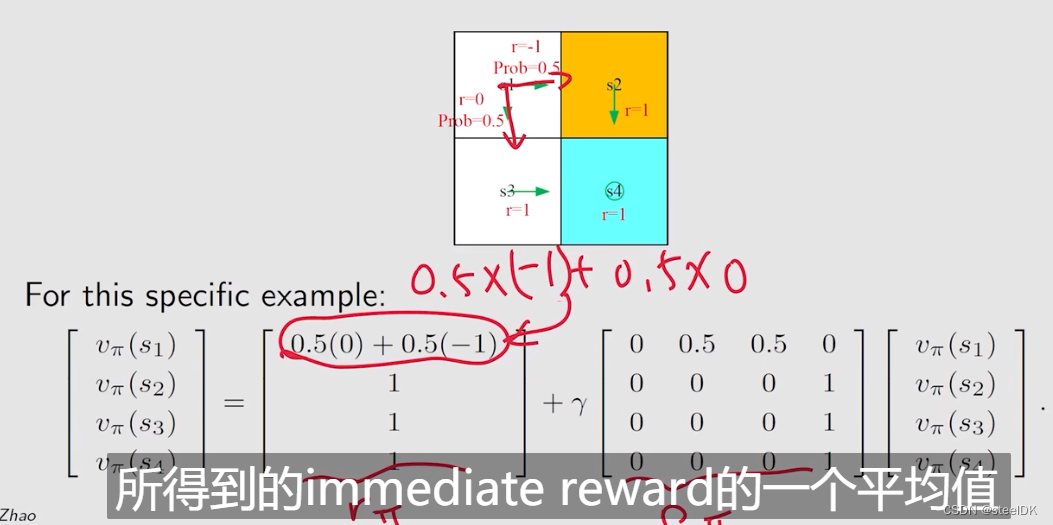
rπ(s)是从当前状态出发,得到了所有immediate reward的平均值。上式红色画的意思是展开相乘。

上图中,[Pπ]ij代表第i行第j列的元素是从si跳到sj的概率,[Pπ]ij这个矩阵也被称为状态转移矩阵。
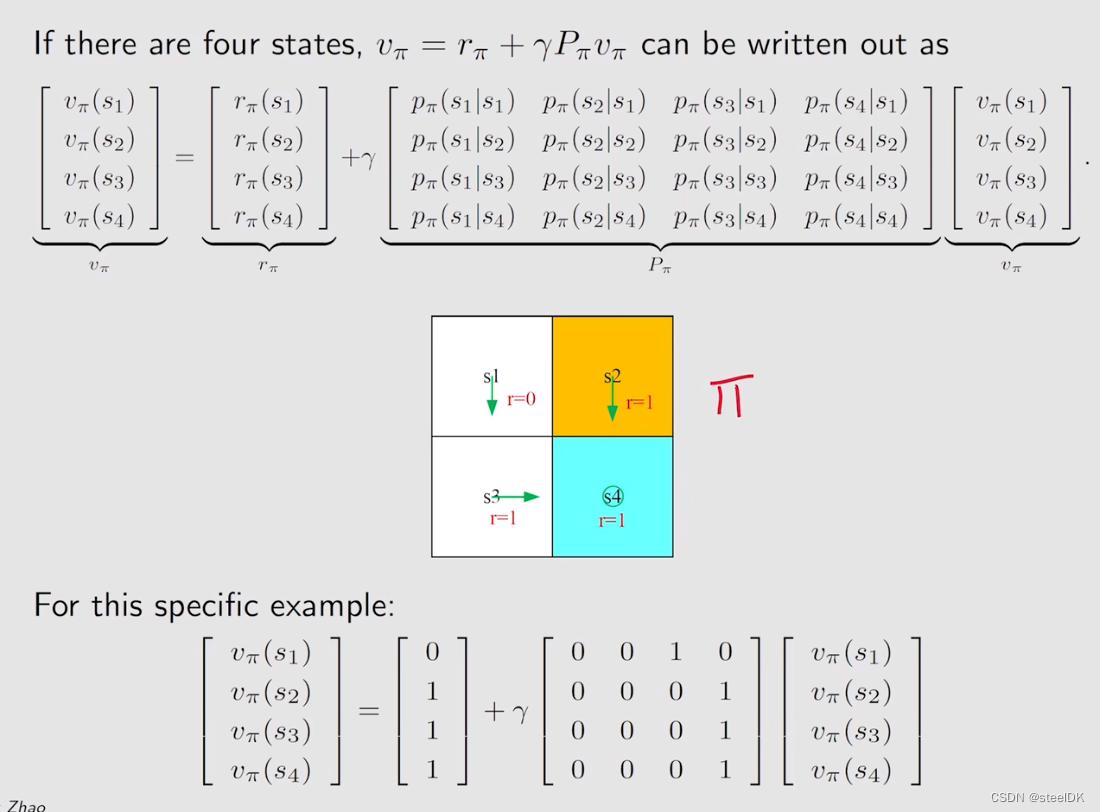
上图是当n=4时,我所得到的matrix-vector 形式,上图中的Pπ就是状态转移矩阵。在举一个例子,见下图:
4、Bellman equation:Solve the state value

首先我们来回答一下为什么要求解state value,实际上给定一个policy,然后我会列出来它的一个贝尔曼公式,再进一步求解贝尔曼公式得到state value,这样的一个过程实际上叫做policy evaluation。policy evaluation是强化学习中非常关键的一个问题,因为我们只有去评价一个策略到底好还是不好,我们才能进一步的去改进它,最后在找到最优的策略,所以求解贝尔曼公式进而得到state value是非常重要的一个问题。

求state value我们给出两种解决方案,第一种就是用求逆矩阵的方法直接求解,但是这种方法通常不会使用,因为当状态空间特别大的时候,矩阵的维度也会特别大,求逆的计算量也会特别大,所以实际当中我们使用的是迭代的方法。iterative solution方法就是从一开始随机猜一个vπ,记为v0,把这个v0带入到上图红色箭头所指的式子中,因为rπ和Pπ都是可以事先知道的,所以可以计算得到v1,然后再把v1带到右边,就又可以得到v2,依次类推,就会得到序列{v0,v1,v2,…vk},实际上我们可以证明当k趋近于无穷的时候,vk就收敛到了vπ,这个vπ就是真实的state value。为什么vk会收敛到vπ呢?下面是证明。

证明的思路是定义vk与vπ之间的误差,证明这个误差趋近于0即可。下面我们通过例子来进一步说明。

上图是两个比较好的policy,可以看到得到的状态值均为正,并且我们还可以看出,不同的策略可以得到相同的value值。下面我们在看两个不好的policy。

通过以上例子可以得出,我们可以计算state value来评价一个策略究竟是好还是坏。
5、Action value
在前几节,我们介绍了state value,以及描述state value的贝尔曼公式,下面我们将从state value转向action value。

state value和action value有什么区别与联系呢?state value指的是agent从一个状态出发,所得到的average return。action value指的是agent从一个状态出发并且选择一个action之后得到的average return。
为什么要关注action value:实际上我们一直讨论的是强化学习中的策略,策略指的是在一个状态我要选择什么样的action,action有很多,具体选择哪一个action就是通过action value来判断,action value大的意味着采取该action能够得到更多的reward。

由上图可知,state value可以和action value建立联系。有很多个action,在当前状态下,采取其中一个action的概率为π(a|s),乘以采取该动作后得到的average return。与π(a|s)相乘的那一项就是action value。


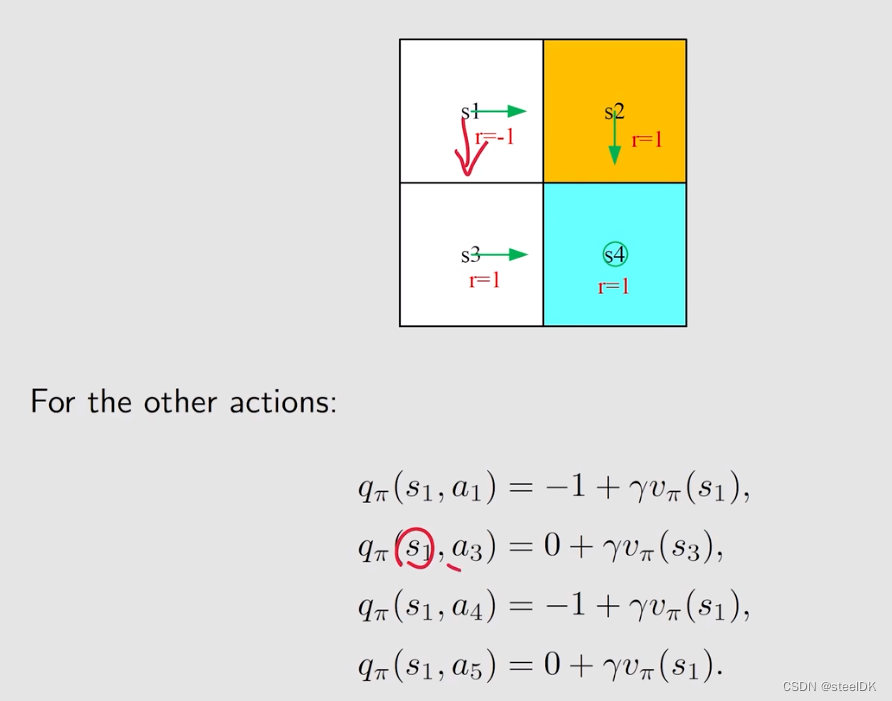
下面通过一个例子来理解action value:
上图中策略已经通过绿色箭头画出来了。
下面做一个总结:

state value满足贝尔曼公式,贝尔曼公式刻画了state value之间的公式,是求解state value的一个工具,上图是它的elementwise form,就是对每一个状态都存在这样一个式子。
这篇关于03 贝尔曼公式的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!









