解析几何专题
【解析几何笔记】8.向量的投影与内积
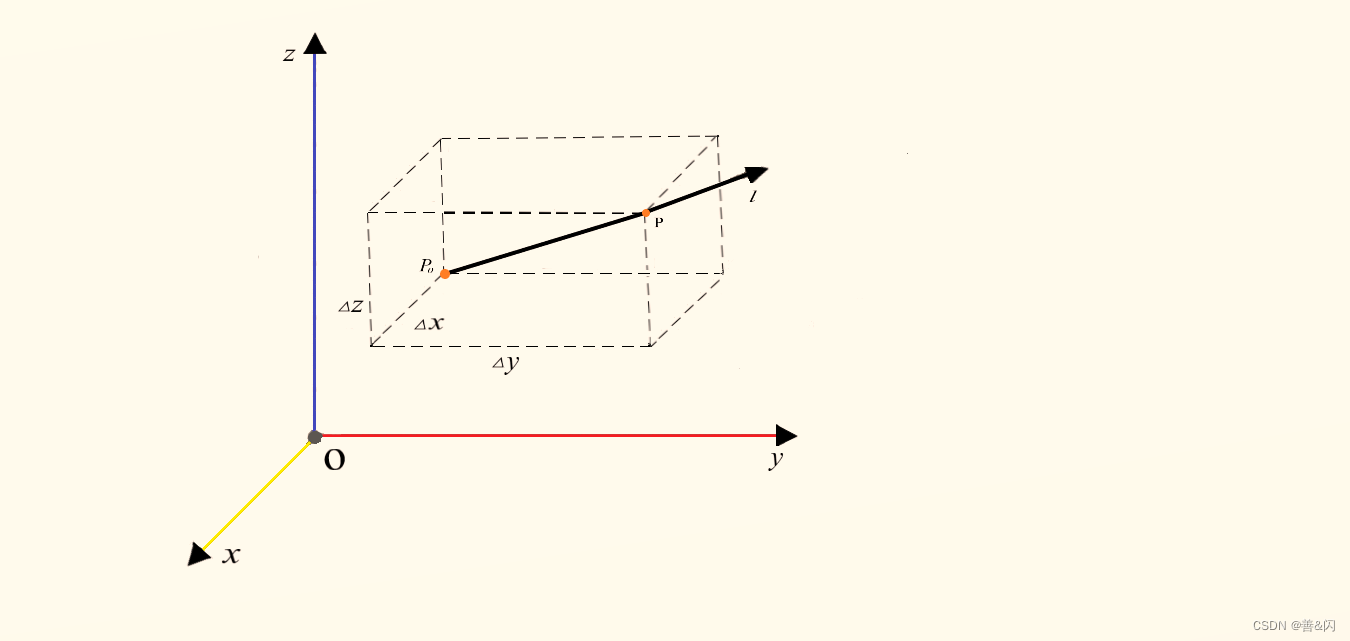
8. 向量的投影与内积 复习前面的知识：，若BCE三点共线，则 A E ⃗ = ( 1 − s ) A B ⃗ + s A C ⃗ , ( B , C , E ) = μ ⇒ s = μ 1 + μ , 1 − s = 1 1 + μ \vec{AE}=(1-s)\vec{AB}+s\vec{AC},(B,C,E)=\mu\Rightarrow s=\frac{\mu}{1+\mu},1-s=
【解析几何笔记】6.三阶行列式
6. 三阶行列式 6.1 三阶行列式的定义 对三阶方阵 ( a 1 a 2 a 3 b 1 b 2 b 3 c 1 c 2 c 3 ) \begin{pmatrix} a_{1} & a_{2} & a_{3}\\ b_{1} & b_{2} & b_{3}\\ c_{1} & c_{2} &c_{3} \end{pmatrix} a1b1c1a2b2c2a3b3c
【数学建模】解析几何与方程模型
文章目录 解析几何与方程模型1.几何建模思想2.Numpy在线性代数中的使用3.国赛求解3.1题目3.2 问题1求解建立模型代码求解 3.3 问题2求解 4.问题答疑Q1:什么是行列式，其使用场景是什么行列式的定义行列式的性质行列式的使用场景 Q2:2023B题问题一用相似三角形求解覆盖宽度 W W W 5.学习感想6.疑问 解析几何与方程模型 写在最前，该读书笔记为参加Da
空间解析几何之直线与平面：推导直线与直线、直线与平面交点
空间解析几何——直线与平面 三维空间中的直线和平面与二维空间中的性质有一定的类似之处，但是其相交关系的求解方式有所差异。本文回顾了三维空间中直线和平面的解析表达，然后推导线-线、线-面交点。 平面 空间平面的表达式为： A x + B y + C z + D = 0 (1) Ax+By+Cz+D=0\tag{1} Ax+By+Cz+D=0(1) 包含了4个参数 A , B , C , D
【分类讨论】【解析几何】【 数学】【推荐】1330. 翻转子数组得到最大的数组值
作者推荐 视频算法专题 本文涉及知识点 分类讨论 解析几何 LeetCode1330. 翻转子数组得到最大的数组值 给你一个整数数组 nums 。「数组值」定义为所有满足 0 <= i < nums.length-1 的 |nums[i]-nums[i+1]| 的和。 你可以选择给定数组的任意子数组，并将该子数组翻转。但你只能执行这个操作 一次 。 请你找到可行的最大 数组值 。 示例
四、空间解析几何（高数）
文章仅作学习记录使用 空间解析几何 四、空间解析几何（高数）1.向量代数（1）数量积（2）向量积（3）混合积（4）向量的方向角和方向余弦 2.空间平面与直线（1）平面方程（2）直线方程（3）位置关系 3.空间曲线与曲面（1）空间曲线（2）空间曲面 4.多元函数微分学的几何应用（1）空间曲线的切线与法平面（2）空间曲面的切平面与法线 5.场论初步（1）方向导数（2）梯度（3）方向导数与梯度的关
管理类联考——数学——真题篇——按知识分类——几何——解析几何
文章目录 解析几何2023真题（2023-07）-几何-解析几何-最值-画图求最值-两线相减求最大-联想三角形的“两边差小于第三边”，当为第三边为最大真题（2023-19）-几何-解析几何-最值-画图求最值-圆方程画出圆的形状-两点间距离型最值=动点在多边形上运动求最值：求 ( x − a ) 2 + ( y − b ) 2 (x-a)^2+(y-b)^2 (x−a)2+(y−b)2最值：设
平面解析几何@平面直线间位置关系及其判定
文章目录 abstract两直线的位置关系用初等代数的知识推导从线性方程组的解的结构推导比值式判定两直线平行重合判定 总结判断位置关系的算法直线平行对应的方程关系👺 特殊相交关系两条直线垂直直线垂直对应的斜率关系直线垂直判断算法直线垂直对应的方程关系 abstract 平面直线间位置关系 讨论直线的相交@重合@平行三种基本关系及其条件直线垂直关系及其条件 两直线的位置关
高等数学教材重难点题型总结（八）向量代数与空间解析几何
同期更新配套的课后题，这部分的题普遍容易，仅对计算能力有一定要求，理解层面没有什么难度。中学立体几何和解析几何掌握不错的同志，这部分只要稍加记忆是没有什么难度的。
管理类联考——数学——汇总篇——知识点突破——几何——解析几何——位置
文章目录 四个点=直线与直线重合、平行相交垂直 两个+无数点=一条线与一个圆无数+无数点=一个圆与一个圆 位置： 四点（两直线）位置：斜率相同与否 四个点=直线与直线 重合、平行、相交、垂直 直线与直线的位置关系，围绕斜截式的斜率“k”和截距“b”展开（一般式可以转为斜截式，或者多记忆一般式的特点）。 当两直线k相等时，看截距b是否相等，是则为重合，否则为平行。 当两直线k不
（数学奥林匹克·命题人讲座系列1）《解析几何》单墫主编 的 读书笔记和选讲 第一讲 直线与圆 1.1 直线（1）知识桥
前言： 作为一名竞赛生，适合的教材是必不可少的，在数学老师的推荐下，接触到了这一系列（共12本），博主将会根据自己的知识，理解和笔记进行选择性的讲解（有一些题目博主就不讲了，同时一些知识介绍部分，博主还是沿用“知识桥”进行选讲，过于简单的知识可能就一笔带过，并且将会使用知识点和题目交替的方式来讲解，也就是一讲知识点，一讲题目和解析），博主的很多笔记都来自数学老师的资料赠与与百度，谷歌等搜索引擎，
![【待补】华中农业大学第五届程序设计大赛 F Escape from the Darkness [解析几何]【数学】](http://acm.hzau.edu.cn/upload/201704/ehint.jpg)
【待补】华中农业大学第五届程序设计大赛 F Escape from the Darkness [解析几何]【数学】
题目链接:http://acm.hzau.edu.cn/problem.php?id=1204 ———————————————————————————————————————— 1204: Escape from the Darkness Time Limit: 1 Sec Memory Limit: 1280 MB Submit: 99 Solved: 3 [Submit][Statu
解析几何北大第五版复习提纲
第一章 两向量向量积 向量积定义：a x b =|a||b|sin几何意义：平行四边形面积性质： 两向量共线的充分必要条件是 a x b = 0 数乘： 分配律： 求法：行列式 三向量混合积 混合积定义：对于一个六面体,边长为a,b,c，则其体积为性质： 三向量共面的充分必要条件是混合积为0交换律 求法：行列式拓展：cram法则 三向量的双重向量积 求法：拓展： 拉格朗日恒等式j
管理类联考——数学——汇总篇——知识点突破——几何——解析几何——记忆
文章目录 考点记忆/考点汇总——按大纲 整体利用目录大纲/记忆宫殿目录大纲记忆宫殿从点出发 局部用各种方法数字编码法归类记忆法重点记忆法歌决记忆法转图像记忆法找出规律法 x \sqrt{x} x 相关公式特殊对称内外切线直线方程直线对称万能公式直线与直线的位置关系 原理推导法点两点中点坐标公式两点距离公式点到直线距离公式两平行直线的距离 直线关于点的对称 可视化法 本篇
向量代数和空间解析几何
个人重点 1.数量积，向量积，混合积 2.平面方程，直线方程，平面与直线的位置关系 (关键：♦♦平面的法线向量，直线的方向向量) 3.求旋转面，柱面方程 概念比较多，p-2020 复习全书 127 容易搞错的一个是向量积的方向交换后加上负号，还有轮换不变号和交换两个变号，还有直线与平面的夹角公式求出来的是sinθ，还有投影曲线不要忘记写另一个参数=0。