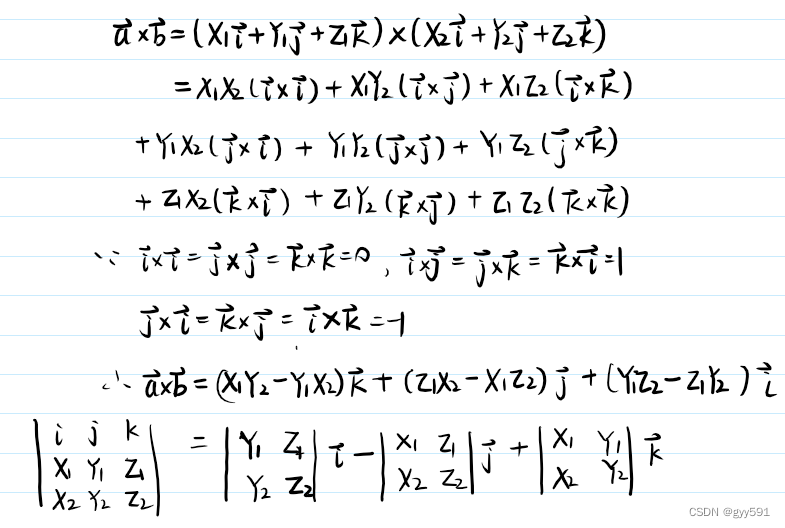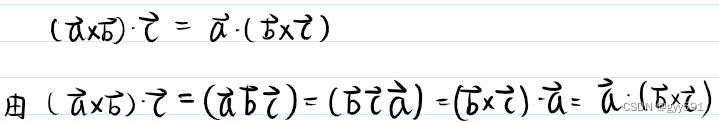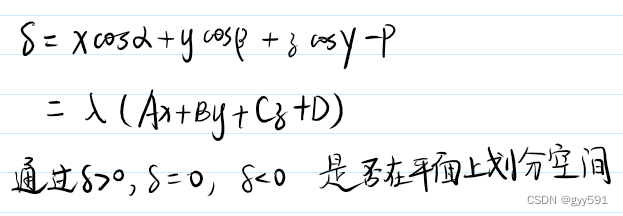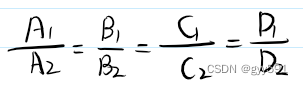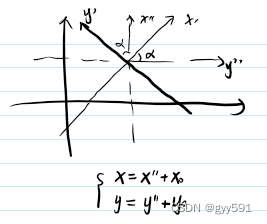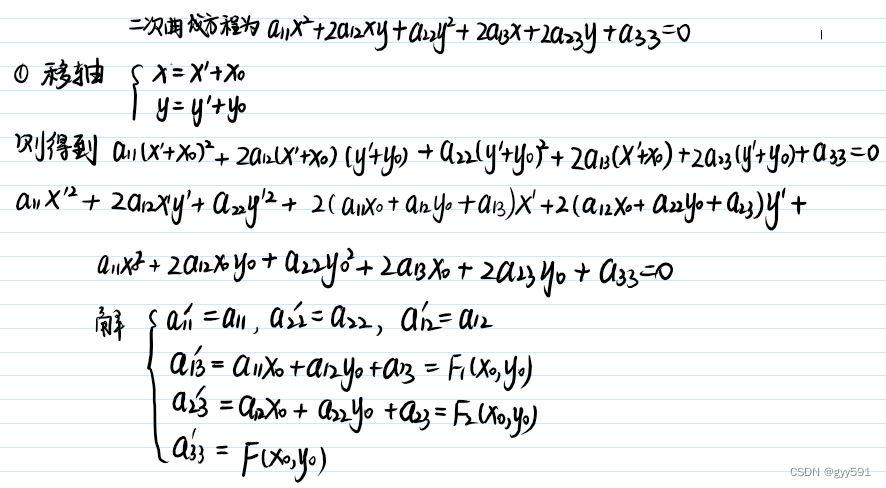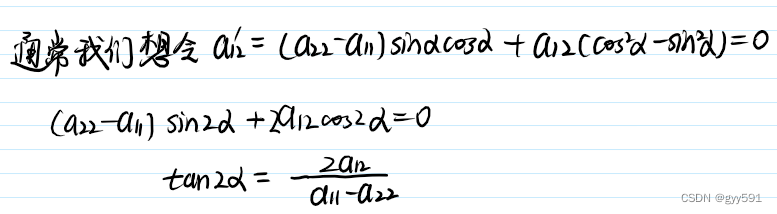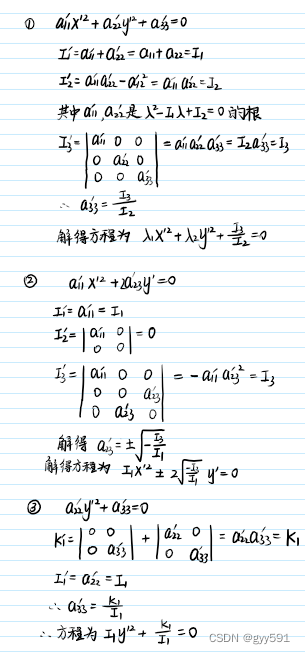本文主要是介绍解析几何北大第五版复习提纲,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
第一章
两向量向量积
- 向量积定义:a x b =|a||b|sin
- 几何意义:平行四边形面积
- 性质:
- 两向量共线的充分必要条件是 a x b = 0
- 数乘:
- 分配律:
- 两向量共线的充分必要条件是 a x b = 0
- 求法:行列式
三向量混合积
- 混合积定义:对于一个六面体,边长为a,b,c,则其体积为

- 性质:
- 三向量共面的充分必要条件是混合积为0

- 交换律
- 三向量共面的充分必要条件是混合积为0
- 求法:行列式
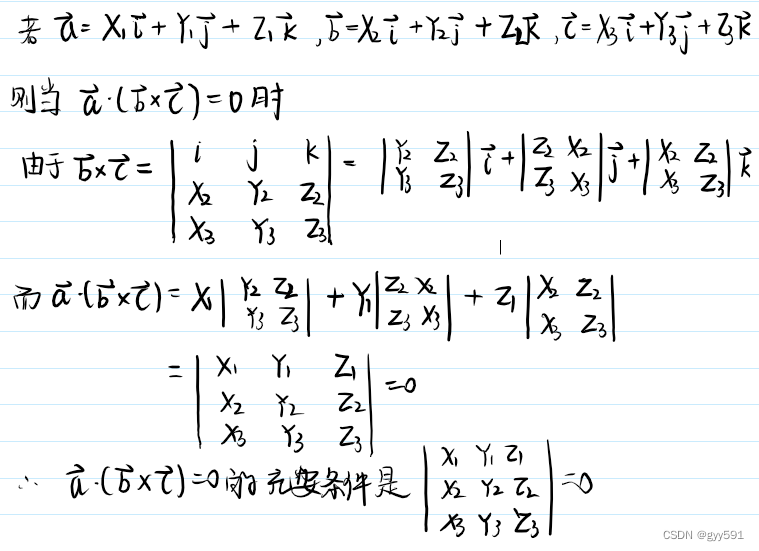
- 拓展:cram法则

三向量的双重向量积
- 求法:
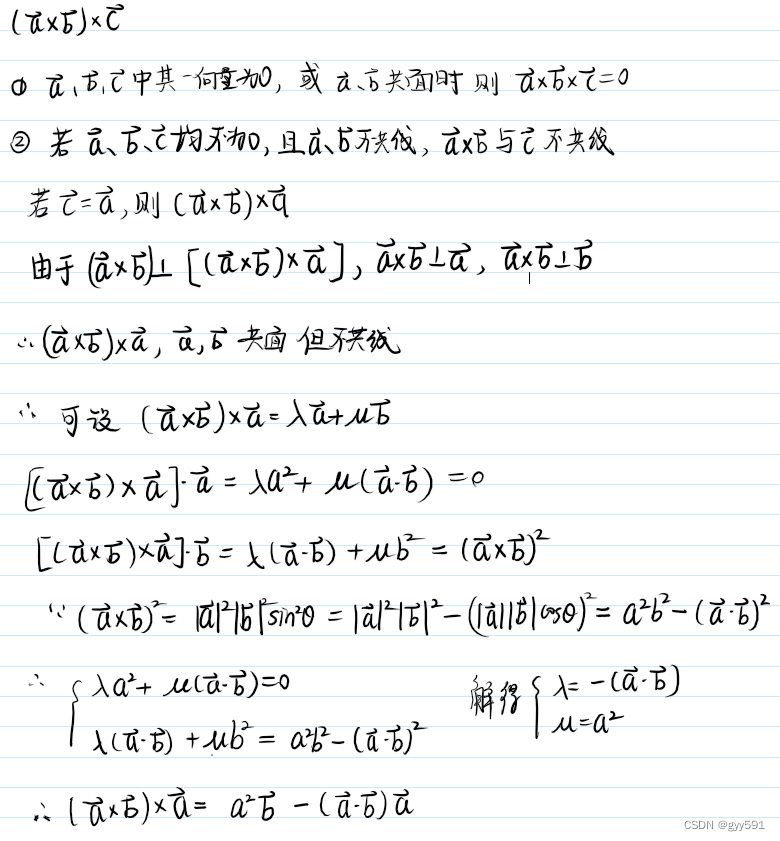
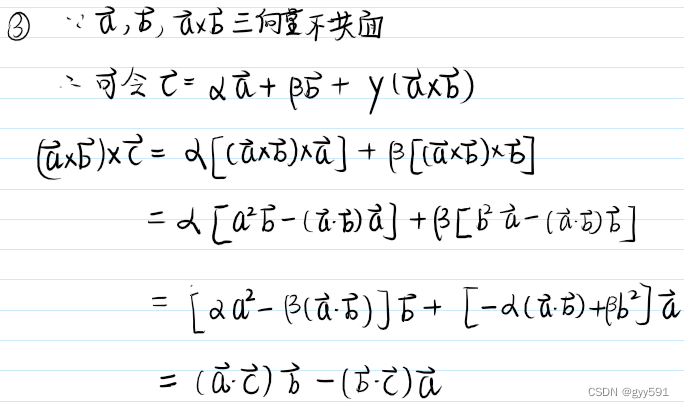
- 拓展:
- 拉格朗日恒等式
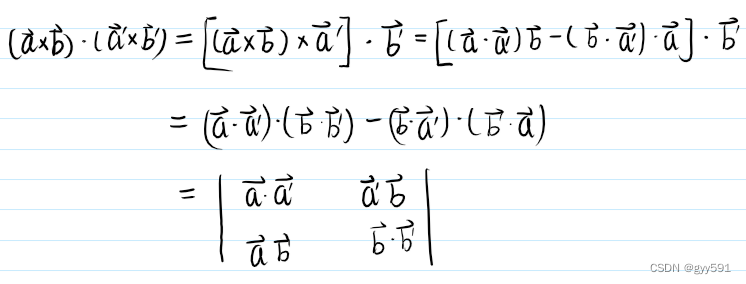
- jacobi恒等式
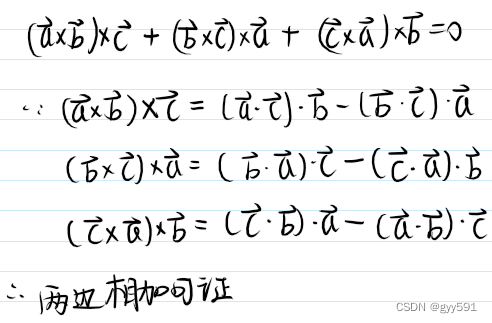
- 拉格朗日恒等式
第二章
平面曲线的方程
- 曲线方程:点满足某方程,点的集合构成曲线
- 向量式参数方程:向径由某个参数决定
- 常见参数方程:
- 外摆线:
- 内摆线:
- 渐展线:
- 外摆线:
曲面的方程
- 曲面的方程:满足方程的点(x,y,z)在曲面上,曲面上的任意一点(x,y,z)满足方程
- 向量式参数方程:空间中向径由2个参数决定的
- 坐标系:
- 直角坐标系:

- 球坐标系:
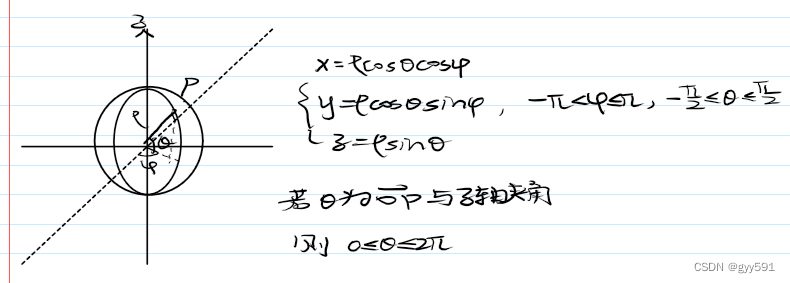
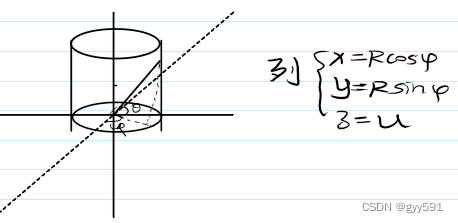
- 柱坐标系:
- 直角坐标系:
空间曲线的方程
- 空间曲线的方程:两个面方程的交集
- 弹簧线方程:

第三章
平面的方程
- 向量式:
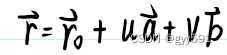
- 点位式:
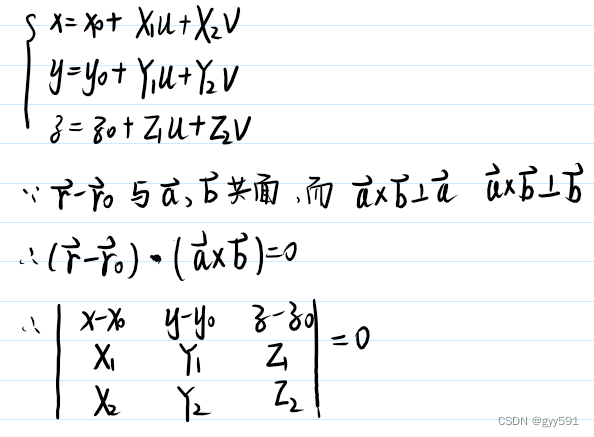
- 三点式:
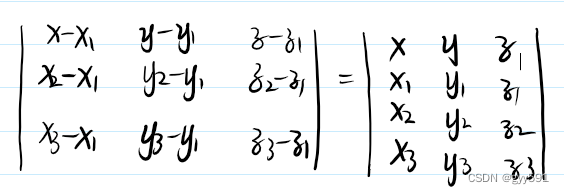
- 一般式:
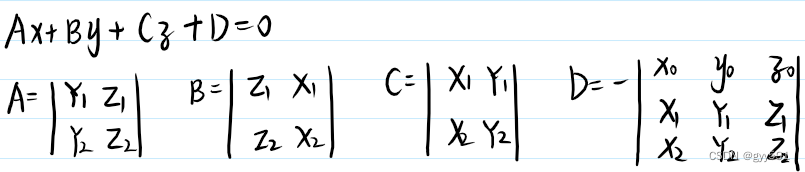
- 截距式:
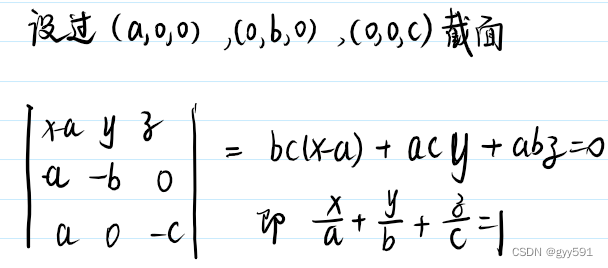
- 点法式:

- 坐标法式:
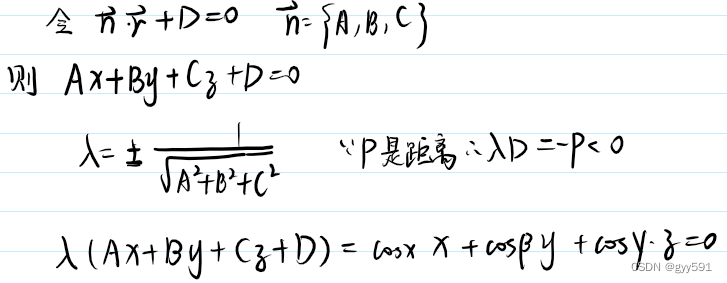
平面与点的相关位置
- 离差:
- 定义:

- 定理:

- 定义:
- 空间划分:
两平面的相关位置
- 二面角:
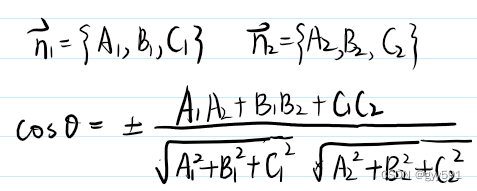
- 相交:
- 垂直:
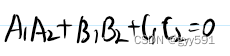
- 垂直:
- 重合:
空间直线的方程
直线与平面的相关位置
空间直线与点的相关位置
空间两直线相关位置
平面束
第四章
柱面
- 柱面:在空间直角坐标系内,空间中定曲线与平行于一条轴的直线相交的生成的曲面叫柱面
- 母线:平行于轴且在柱面内的直线
- 准线:定曲线
- 方程:
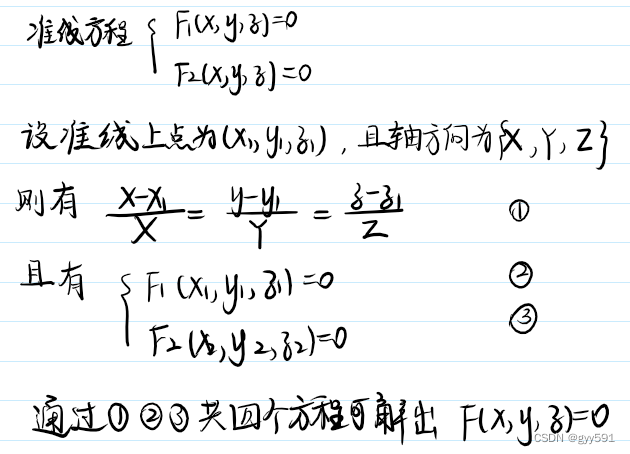
- 定理:柱面方程中缺省哪个值,方程就平行于哪个轴
- 投影柱面、投影曲线:对应面和对应缺省轴的柱面方程的交
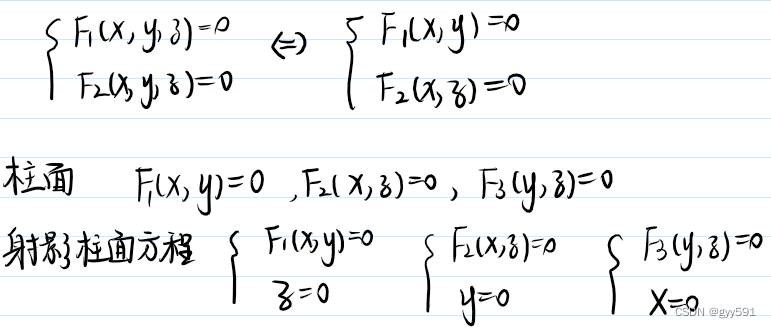
锥面
- 锥面:空间中过一定点的直线束与定曲线相交形成的曲面叫作锥面
- 母线:锥面中过定点的直线
- 准线:定曲线
- 一个关于x,y,z的齐次方程是过原点的锥面
- 证明:
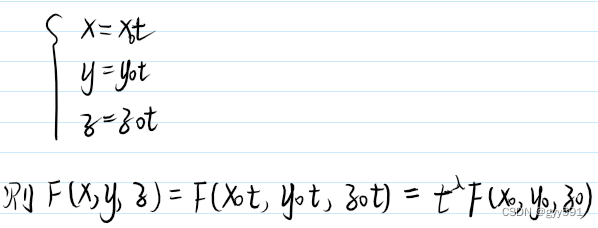
- 推论:关于x-x0,y-y0,z-z0的齐次方程是过x0,y0,z0的锥面
- 证明:
旋转曲面
- 旋转曲面:在直角坐标系中,一曲线绕一直线转动形成的曲面。
- 母线:绕转的曲线
- 准线:垂直母线的纬圆
- 方程:
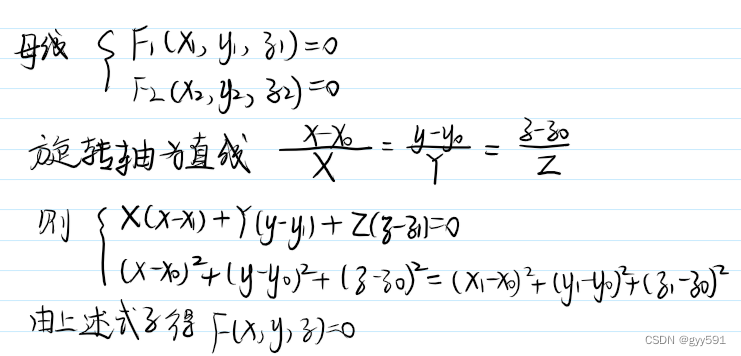
- 绕轴旋转的曲线方程:曲线绕哪轴,哪轴不变,另一变量利用其余变量的和的平方根代替

4.7单叶双曲面与双曲抛物面的直母线
- 直纹曲面:由一族直线旋转而成的曲面,有椭圆、锥面、单叶双曲面和双曲抛物面
- 直母线定义:可以通过一族直线旋转得到曲面,该族直线就是直母线
- 方程:
- 单叶双曲面:
- 直母线方程:

- 推论:
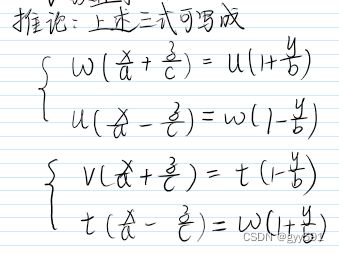
- 双曲抛物面:
- 直母线方程:

- 问题:此处为何没有用两个参数表示?

- 单叶双曲面:
- 定理:
- 单叶双曲面的直母线相交且共面

-
- 单叶双曲面的同族直母线异面,双叶抛物面的同族全体直母线平行于同一平面
二次曲线的一般理论
一般理论
- 实点:(x,y)坐标都是实数
- 虚点:(x,y)其中一个坐标是虚数
- 共轭虚点:坐标分别对应共轭,共轭虚点的中点是实点
- 复点:实点和虚点都是复点
- 二次曲线方程:

- 直线方程:

- 方程合并:
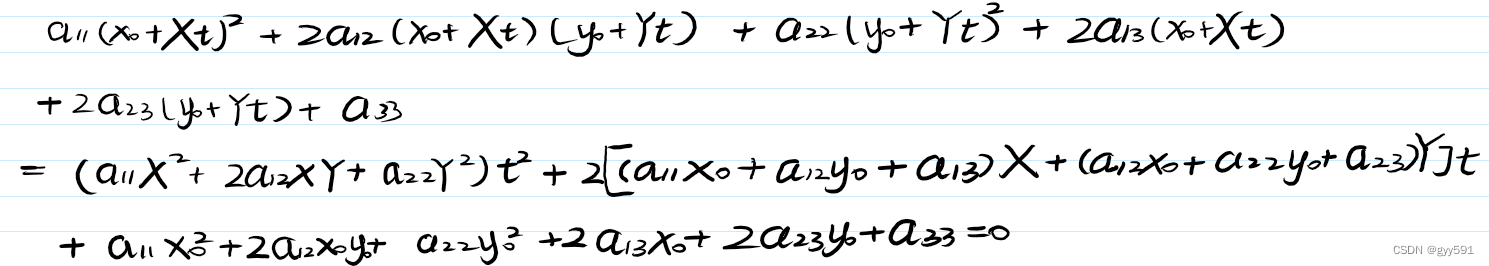
- 相关标记:
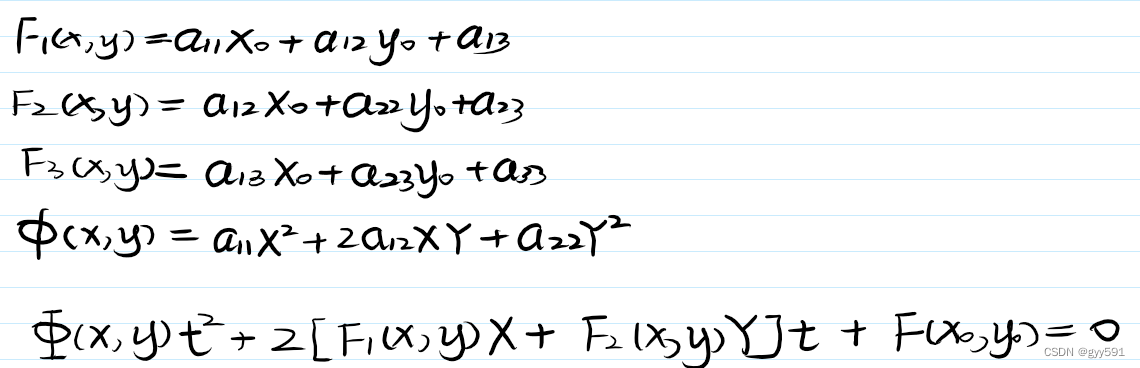
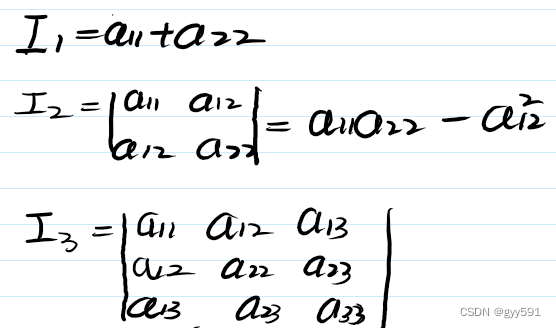
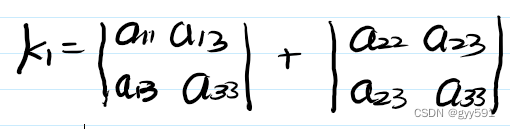
二次曲线与直线相关位置
- 二次曲线与直线合并方程:

- 位置关系:

二次曲线的渐近方向、中心、渐近线
- 渐近方向:当
(x,y)=0时,X:Y为渐近方向
- 渐近方向求解:

- 求解分析:

- 渐近方向求解:
- 中心:二次曲线的对称中心
- 中心求解方法:

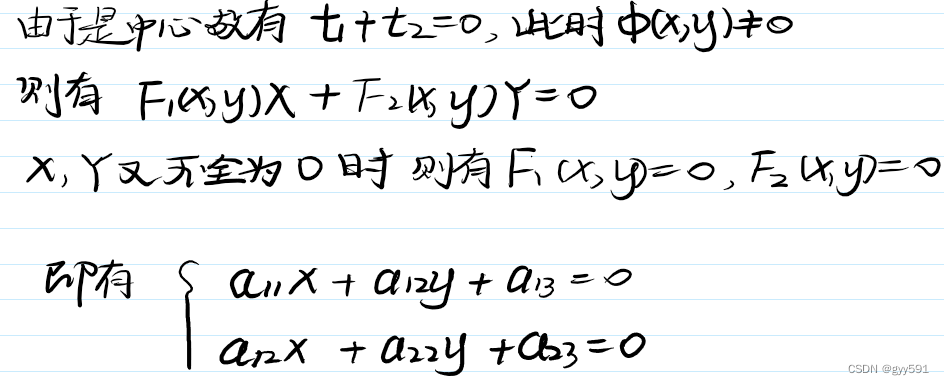
- 三种二次曲线:

- 渐近线:过二次曲线中心且方向为渐近方向的直线
- 渐近线定理:二次曲线的渐近线要么与二次曲线无交点,要么整条渐近线都在二次曲线上
- 证明:
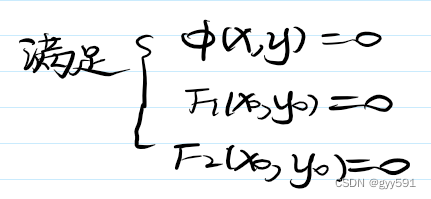
- 所以根据二次曲线和直线位置关系知,如果F(x0,y0)=0则渐近线在二次曲线上,否则与二次曲线无交点。
二次曲线的切线
- 切线定义:直线与二次曲线相交于一个重合的点,这个点就是切点,直线就是切线;如果直线全部在二次曲线上则直线上任意一点都是切点。
- 切线求法:
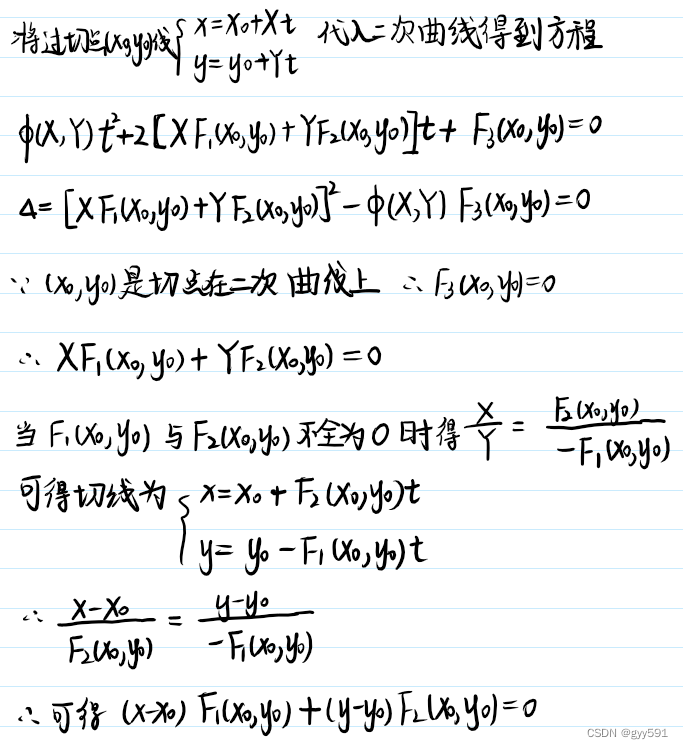
- 奇异点、正则点:

- 切线公式:
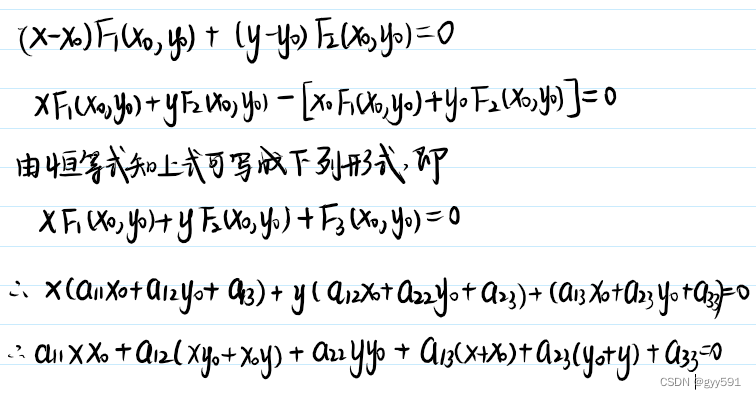
二次曲线的直径
- 直径:二次曲线共轭弦的中点连成一条直线叫直径。

- 条件:弦方向不能是渐近方向,否则不可能有两个交点
- 相关推导:

- 分类:
- 共轭直径、共轭弦:一组平行弦的中点的轨迹叫作直径,这组平行弦叫共轭弦。与共轭弦方向相同的直径与共轭弦的直径组成一对共轭直径。
- 性质:
- 中心二次曲线的非渐近方向的共轭方向是非渐近方向,非中心二次曲线的渐近方向的共轭方向是共轭方向。
- 共轭方向间满足关系:
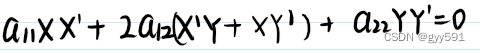
- 推导:
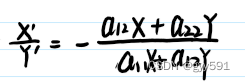 展开即可。
展开即可。
- 推导:
- 中心二次曲线的非渐近方向的共轭方向是非渐近方向,非中心二次曲线的渐近方向的共轭方向是共轭方向。
- 性质:
二次曲线的主直径和主方向
- 主直径:弦与直径互相垂直,则该直径为主直径。主直径的共轭直径也是主直径。
- 求法推导:

- 性质:
- 特征方程的根都是实数

二次曲线的方程化简与分类
- 直线方程
- 移轴:
-
- 转轴:
- 二次曲线
- 移轴:
- 转轴:
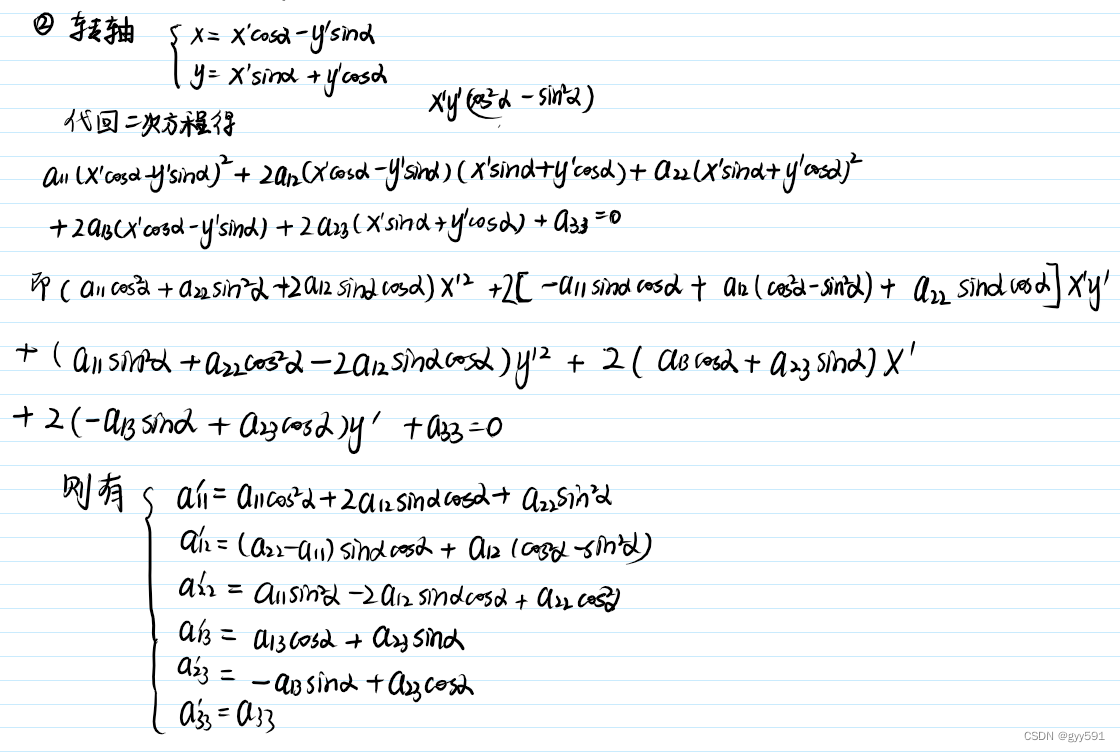
- 转轴角:
- 转轴方向实际上是主方向
- 移轴:
- 分类:
应用不变量化简二次曲线方程
- 不变量、半不变量:二次曲线中的系数经过某个函数没有发生变化,这个函数叫不变量,只是经过转轴不变叫半不变量。
- 存在区域:
- 移轴:
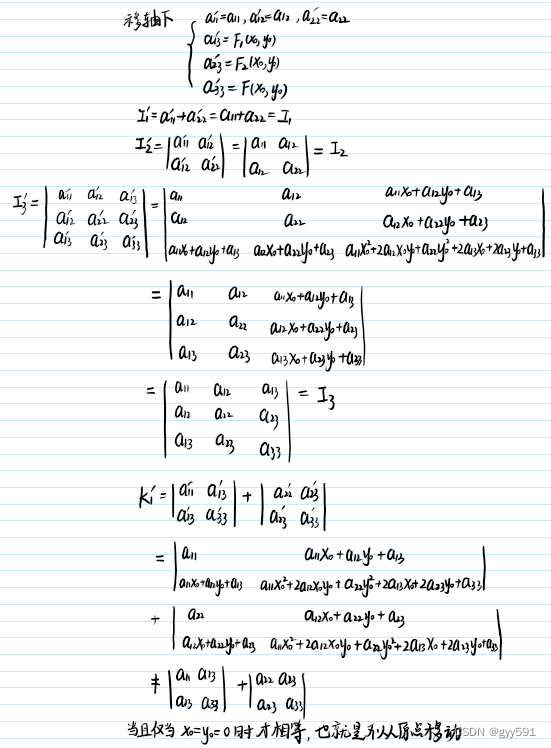
- 转轴:


- 线心二次曲线在移轴下K1也是不变量
- 应用不变量化简二次方程
- 利用不变量判断二次曲线类型
这篇关于解析几何北大第五版复习提纲的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!