本文主要是介绍(数学奥林匹克·命题人讲座系列1)《解析几何》单墫主编 的 读书笔记和选讲 第一讲 直线与圆 1.1 直线(1)知识桥,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
前言:
作为一名竞赛生,适合的教材是必不可少的,在数学老师的推荐下,接触到了这一系列(共12本),博主将会根据自己的知识,理解和笔记进行选择性的讲解(有一些题目博主就不讲了,同时一些知识介绍部分,博主还是沿用“知识桥”进行选讲,过于简单的知识可能就一笔带过,并且将会使用知识点和题目交替的方式来讲解,也就是一讲知识点,一讲题目和解析),博主的很多笔记都来自数学老师的资料赠与与百度,谷歌等搜索引擎,如果有所谬误,请多多指教,在这里放一张书面封面图片,以防弄混淆了

数学奥林匹克·命题人讲座系列第一本 《解析几何》
那我们正式开始吧!
第一讲:直线与圆
这一讲分为两个部分,1.1直线与1.2圆的方程
知识汇总:
1.倾斜角:当直线
与
轴相交时,
轴绕着交点按逆时针方向旋转到和
重合时所转过的最小正角为
2.斜率:
=
, 当
为
时,无斜率(直线无斜率)
3.两点斜率公式:两点则斜率
=
直线的方程有很多种类,点斜式,斜截式,两点式,截距式,参数式,一般式和法线式
| 形式 | 适用范围 | 斜率 | |
| 点斜式 | 不能表示与x轴垂直的直线 | k | |
| 斜截式 | 不能表示与x轴垂直的直线 | k | |
| 两点式 | |||
| 截距式 | 不能表示与x轴和y轴垂直的直线,也不能表示过原点的直线 | ||
| 参数式 | 任何直线都能标示 | ||
| 一般式 | A,B不能同时为0,任何直线都能表示 | ||
| 法线式 |
*参数式可以有很多形式,其中的a和b可以被cosa和sina代替,也可以设直线过点则该直线上的动点
的坐标满足该形式
,此时M的分线段M1,M2的比为
3. 两直线平行和垂直的充要条件
若两直线平行,则无解,若无解,则两直线平行,此时两直线斜率一样,所以
若两直线垂直,则
4.点线距离公式(两点距离公式过于简单,在此不再赘述):点到直线l:Ax+By+C=0的距离为
5.两平行线距离公式(两直线分别为和
):
6.两直线夹角:当时,


这已经是我三年前的笔记了,有的已经忘记当时是怎么想的了[哭笑不得]其余的定理,其实可以自证试一试看,都比较简单
7.施泰纳-莱赫姆斯(Steiner-Lehmus)角平分线定理
两个底角平分线相等的三角形是等腰三角形(个人感觉有点显然[实则不然])
它的证明:
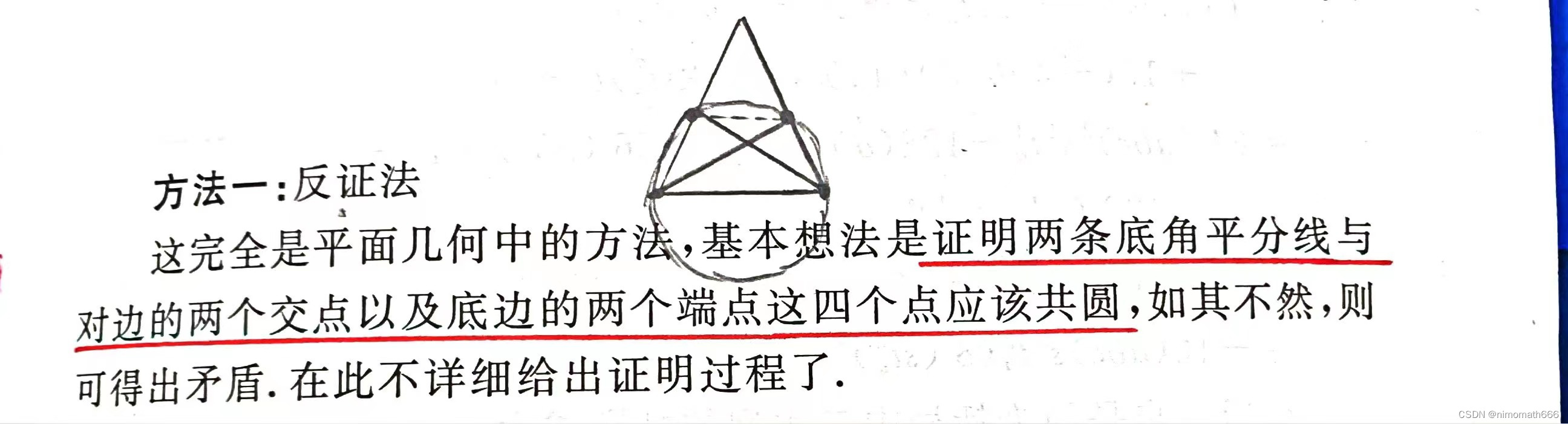
最为简单的方法,没有之一

使用了角平分线长公式,该公式可以使用斯特瓦尔特定理去证明,而斯特瓦尔特的证明如图
当然有时间和有兴趣的人可以试一试三角法和建系的做法(PS:我一开始不喜欢用建系的方法,后来发现,嗯,确实好用,简单直接)

8.简单线性规划

总结
这是我们解析几何的第一讲,后续第二讲将会是和直线有关的例题,有意向者可以试一试,谢谢读者们的阅读
这篇关于(数学奥林匹克·命题人讲座系列1)《解析几何》单墫主编 的 读书笔记和选讲 第一讲 直线与圆 1.1 直线(1)知识桥的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!








