本文主要是介绍管理类联考——数学——汇总篇——知识点突破——几何——解析几何——记忆,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 考点
- 记忆/考点汇总——按大纲
- 整体利用目录大纲/记忆宫殿
- 目录大纲
- 记忆宫殿
- 从点出发
- 局部用各种方法
- 数字编码法
- 归类记忆法
- 重点记忆法
- 歌决记忆法
- 转图像记忆法
- 找出规律法
- x \sqrt{x} x相关公式
- 特殊对称
- 内外切线
- 直线方程
- 直线对称万能公式
- 直线与直线的位置关系
- 原理推导法
- 点
- 两点中点坐标公式
- 两点距离公式
- 点到直线距离公式
- 两平行直线的距离
- 直线关于点的对称
- 可视化法
本篇思路:根据各方的资料,比如名师的资料,按大纲或者其他方式,收集/汇总考点,即需记忆点,在通过整体的记忆法,比如整体信息很多,通常使用记忆宫殿法,绘图记忆法进行记忆,针对局部/细节/组成的部分,可通过多种方法,比如联想记忆法、理解记忆法等进行进一步记忆。
考点
通过汇总各方大佬资料,作为收集考点/记忆点的信息输入:XX,收集汇总如下:
记忆/考点汇总——按大纲
——点——
两点中点坐标:两点 P 1 ( x 1 , y 1 ) P_1(x_1,y_1) P1(x1,y1)与 P 2 ( x 2 , y 2 ) P_2(x_2,y_2) P2(x2,y2)的中点坐标为( x 1 + x 2 2 , y 1 + y 2 2 \frac{x_1+x_2}{2},\frac{y_1+y_2}{2} 2x1+x2,2y1+y2)
两点距离公式:两点 A ( x 1 , y 1 ) A(x_1,y_1) A(x1,y1)与 B ( x 2 , y 2 ) B(x_2,y_2) B(x2,y2)之间的距离 d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} d=(x2−x1)2+(y2−y1)2
两点斜率公式:设直线 l l l上有两个点 P 1 ( x 1 , y 1 ) P_1(x_1,y_1) P1(x1,y1), P 2 ( x 2 , y 2 ) P_2(x_2,y_2) P2(x2,y2),则直线 l l l的斜率 k = y 2 − y 1 x 2 − x 1 ( x 1 ≠ x 2 ) k=\frac{y_2-y_1}{x_2-x_1}(x_1≠x_2) k=x2−x1y2−y1(x1=x2)
——线——
斜率: k = t a n α k=tanα k=tanα, ( α ≠ π 2 ) (α≠\frac{π}{2}) (α=2π),当 α ∈ [ 0 , π 2 ) α∈[0,\frac{π}{2}) α∈[0,2π)时, k ∈ [ 0 , + ∞ ) k∈[0,+∞) k∈[0,+∞);当 α = π 2 α=\frac{π}{2} α=2π时,直线的斜率不存在;当 α ∈ ( π 2 , π ) α∈(\frac{π}{2},π) α∈(2π,π)时, k ∈ ( − ∞ , 0 ) k∈(-∞,0) k∈(−∞,0)。直线的斜率反映了直线对x轴的倾斜程度。
直线方程斜截式:若已知斜率k和y轴截距b,直线可表示为 y = k x + b y=kx+b y=kx+b
直线方程点斜式:若已知斜率k和某点( x 0 , y 0 x_0,y_0 x0,y0),直线可表示 y = y 0 + k ( x − x 0 ) y=y_0+k(x-x_0) y=y0+k(x−x0)或 y − y 0 x − x 0 = k \frac{y-y_0}{x-x_0}=k x−x0y−y0=k
直线方程截距式:若已知x轴和y轴截距分别为a,b,直线可表示为 x a + y b = 1 \frac{x}{a}+\frac{y}{b}=1 ax+by=1
直线方程两点式:若已知两点坐标( x 1 , y 1 x_1,y_1 x1,y1),( x 2 , y 2 x_2,y_2 x2,y2),直线可表示为 x − x 1 x 2 − x 1 = y − y 1 y 2 − y 1 \frac{x-x_1}{x_2-x_1}=\frac{y-y_1}{y_2-y_1} x2−x1x−x1=y2−y1y−y1
直线方程一般式: a x + b y + c = 0 ax+by+c=0 ax+by+c=0——【一次函数】
——距离——
点到直线的距离公式: l : a x + b y + c = 0 l:ax+by+c=0 l:ax+by+c=0,点( x 0 , y 0 x_0,y_0 x0,y0)到 l l l的距离为 d = ∣ a x 0 + b y 0 + c ∣ a 2 + b 2 d=\frac{|ax_0+by_0+c|}{\sqrt{a^2+b^2}} d=a2+b2∣ax0+by0+c∣
两平行直线之间的距离公式: l 1 : a x + b y + c 1 = 0 l_1:ax+by+c_1=0 l1:ax+by+c1=0; l 2 : a x + b y + c 2 = 0 l_2:ax+by+c_2=0 l2:ax+by+c2=0,那么 l 1 l_1 l1与 l 2 l_2 l2之间的距离为 d = ∣ c 1 − c 2 ∣ a 2 + b 2 d=\frac{|c_1-c_2|}{\sqrt{a^2+b^2}} d=a2+b2∣c1−c2∣
——位置——
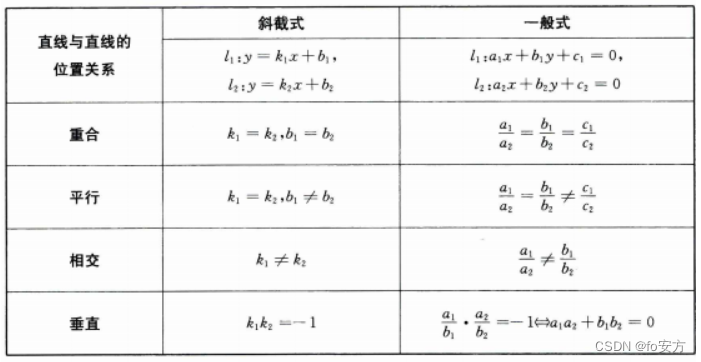
两直线位置关系:斜截式: l 1 : y = k 1 x + b 1 l_1:y=k_1x+b_1 l1:y=k1x+b1, l 2 : y = k 2 x + b 2 l_2:y=k_2x+b_2 l2:y=k2x+b2
重合: l 1 / / l 2 l_1//l_2 l1//l2 ⟺ \Longleftrightarrow ⟺ k 1 = k 2 , b 1 = b 2 k_1=k_2,b_1=b_2 k1=k2,b1=b2——【重合为两条直线斜率相等且截距相等】
平行: l 1 / / l 2 l_1//l_2 l1//l2 ⟺ \Longleftrightarrow ⟺ k 1 = k 2 , b 1 ≠ b 2 k_1=k_2,b_1≠b_2 k1=k2,b1=b2——【平行为两条直线斜率相等但截距不相等】
相交: k 1 ≠ k 2 k_1≠k_2 k1=k2——【相交为两条直线的斜率不相等】
垂直: l 1 ⊥ l 2 l_1 \bot l_2 l1⊥l2 ⟺ \Longleftrightarrow ⟺ k 1 k 2 = − 1 k_1k_2=-1 k1k2=−1或者 k 1 = 0 k_1=0 k1=0, k 2 k_2 k2不存在(l垂直与x轴)——【垂直分两种,一是斜率存在且乘积为-1;二是一条斜率不存在,一条斜率为0,即一条平行x轴,一条平行y轴】
两直线位置关系:一般式: l 1 : a 1 x + b 1 y + c 1 = 0 l_1:a_1x+b_1y+c_1=0 l1:a1x+b1y+c1=0, l 2 : a 2 x + b 2 y + c 2 = 0 l_2:a_2x+b_2y+c_2=0 l2:a2x+b2y+c2=0
平行: l 1 / / l 2 l_1//l_2 l1//l2 ⟺ \Longleftrightarrow ⟺ a 1 a 2 = b 1 b 2 = c 1 c 2 \frac{a_1}{a_2}=\frac{b_1}{b_2}=\frac{c_1}{c_2} a2a1=b2b1=c2c1
平行: l 1 / / l 2 l_1//l_2 l1//l2 ⟺ \Longleftrightarrow ⟺ a 1 a 2 = b 1 b 2 ≠ c 1 c 2 \frac{a_1}{a_2}=\frac{b_1}{b_2}≠\frac{c_1}{c_2} a2a1=b2b1=c2c1
相交: a 1 a 2 ≠ b 1 b 2 \frac{a_1}{a_2}≠\frac{b_1}{b_2} a2a1=b2b1
垂直: l 1 ⊥ l 2 l_1 \bot l_2 l1⊥l2 ⟺ \Longleftrightarrow ⟺ a 1 b 1 ⋅ a 2 b 2 = − 1 \frac{a_1}{b_1}·\frac{a_2}{b_2}=-1 b1a1⋅b2a2=−1 ⟺ \Longleftrightarrow ⟺ a 1 a 2 + b 1 b 2 = 0 a_1a_2+b_1b_2=0 a1a2+b1b2=0——【】
点与直线位置关系:点( x 0 , y 0 x_0,y_0 x0,y0),直线 l : y = k x + b l:y=kx+b l:y=kx+b
y 0 = { > k x 0 + b , 点在直线上方 = k x 0 + b , 点在直线上 < k x 0 + b , 点在直线下方 y_0 = \begin{cases} >kx_0+b, & \text{点在直线上方} \\ =kx_0+b, & \text{点在直线上} \\ <kx_0+b, & \text{点在直线下方} \end{cases} y0=⎩ ⎨ ⎧>kx0+b,=kx0+b,<kx0+b,点在直线上方点在直线上点在直线下方
圆的方程标准式:圆心为( x 0 , y 0 x_0,y_0 x0,y0),半径为r的圆可表示为 ( x − x 0 ) 2 + ( y − y 0 ) 2 = r 2 (x-x_0)^2+(y-y_0)^2=r^2 (x−x0)2+(y−y0)2=r2
圆的方程一般式: x 2 + y 2 + a x + b y + c = 0 x^2+y^2+ax+by+c=0 x2+y2+ax+by+c=0,可将其配方变为标准式: ( x + a 2 ) 2 + ( y + b 2 ) 2 = a 2 + b 2 − 4 c 4 (x+\frac{a}{2})^2+(y+\frac{b}{2})^2=\frac{a^2+b^2-4c}{4} (x+2a)2+(y+2b)2=4a2+b2−4c = a 2 + b 2 − 4 c 4 =\frac{\sqrt{a^2+b^2-4c}}{4} =4a2+b2−4c
{ a 2 + b 2 − 4 c > 0 , 方程表示一个圆 a 2 + b 2 − 4 c = 0 , 方程表示一个点 a 2 + b 2 − 4 c < 0 , 方程无意义 \begin{cases} a^2+b^2-4c>0, & \text{方程表示一个圆} \\ a^2+b^2-4c=0, & \text{方程表示一个点} \\ a^2+b^2-4c<0, & \text{方程无意义} \end{cases} ⎩ ⎨ ⎧a2+b2−4c>0,a2+b2−4c=0,a2+b2−4c<0,方程表示一个圆方程表示一个点方程无意义
点与圆的位置关系:点在圆内、点在圆上、点在圆外。设点 P ( x 0 , y 0 ) P(x_0,y_0) P(x0,y0),圆: ( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 (x−a)2+(y−b)2=r2,则有:
{ ( x 0 − a ) 2 + ( y 0 − b ) 2 < r 2 , 点在圆内 ( x 0 − a ) 2 + ( y 0 − b ) 2 = r 2 , 点在圆上 ( x 0 − a ) 2 + ( y 0 − b ) 2 > r 2 , 点在圆外 \begin{cases} (x_0-a)^2+(y_0-b)^2<r^2, & \text{点在圆内} \\ (x_0-a)^2+(y_0-b)^2=r^2, & \text{点在圆上} \\ (x_0-a)^2+(y_0-b)^2>r^2, & \text{点在圆外} \end{cases} ⎩ ⎨ ⎧(x0−a)2+(y0−b)2<r2,(x0−a)2+(y0−b)2=r2,(x0−a)2+(y0−b)2>r2,点在圆内点在圆上点在圆外
直线与圆的位置关系:
相切:求圆的切线方程时,常设切线的方程为 A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0或 y = k ( x − a ) + b y=k(x-a)+b y=k(x−a)+b,再利用点到直线的距离等于半径,即可确定切线方程。过圆 ( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 (x−a)2+(y−b)2=r2上的一点 P ( x 0 , y 0 ) P(x_0,y_0) P(x0,y0)作圆的切线,则切线方程为 ( x − a ) ( x 0 − a ) + ( y − b ) ( y 0 − b ) = r 2 (x-a)(x_0-a)+(y-b)(y_0-b)=r^2 (x−a)(x0−a)+(y−b)(y0−b)=r2。若点P在圆外,则上述方程为过点P作圆的两条切线,形成的两个切点所在的直线的方程。
相交:设圆心到直线的距离为d,圆的半径为r,则直线与圆相交时,直线被圆截得的弦长为 l = 2 r 2 − d 2 l=2\sqrt{r^2-d^2} l=2r2−d2
相离:圆上的点与直线之间的距离问题,一般是求满足条件的点的个数,点的个数通常有4种,为1个点,2个点,3个点,4个点。其中,1个点,3个点的情况是临界点,优先考虑临界点的情况。
坐标:已知圆的一般方程: x 2 + y 2 + D x + E y + F = 0 x^2+y^2+Dx+Ey+F=0 x2+y2+Dx+Ey+F=0,根据此式整理出圆的标准方程为 ( x + D 2 ) 2 + ( y + E 2 ) 2 = D 2 + E 2 − 4 F 4 (x+\frac{D}{2})^2+(y+\frac{E}{2})^2=\frac{D^2+E^2-4F}{4} (x+2D)2+(y+2E)2=4D2+E2−4F,即圆心坐标为( − D 2 -\frac{D}{2} −2D,- E 2 \frac{E}{2} 2E),半径为 r = D 2 + E 2 − 4 F 4 r=\sqrt{\frac{D^2+E^2-4F}{4}} r=4D2+E2−4F,故圆与坐标轴的关系为
①圆与x轴相切:圆心纵坐标的绝对值为r,即 ∣ − E 2 ∣ = D 2 + E 2 − 4 F 4 |-\frac{E}{2}|=\sqrt{\frac{D^2+E^2-4F}{4}} ∣−2E∣=4D2+E2−4F
②圆与y轴相切:圆心横坐标的绝对值为r,即 ∣ − D 2 ∣ = D 2 + E 2 − 4 F 4 |-\frac{D}{2}|=\sqrt{\frac{D^2+E^2-4F}{4}} ∣−2D∣=4D2+E2−4F
③圆与坐标轴无交点:圆心纵坐标的绝对值大于r且横坐标的绝对值大于r。
平移:对曲线进行平移,其方程有如下变化:
①曲线 y = f ( x ) y=f(x) y=f(x),向上平移a个单位( a > 0 a>0 a>0),方程变为 y = f ( x ) + a y=f(x)+a y=f(x)+a;
②曲线 y = f ( x ) y=f(x) y=f(x),向下平移a个单位( a > 0 a>0 a>0),方程变为 y = f ( x ) − a y=f(x)-a y=f(x)−a;
③曲线 y = f ( x ) y=f(x) y=f(x),向左平移a个单位( a > 0 a>0 a>0),方程变为 y = f ( x + a ) y=f(x+a) y=f(x+a);
④曲线 y = f ( x ) y=f(x) y=f(x),向右平移a个单位( a > 0 a>0 a>0),方程变为 y = f ( x − a ) y=f(x-a) y=f(x−a)。——【歌诀记忆法:上加下减,左加右减】
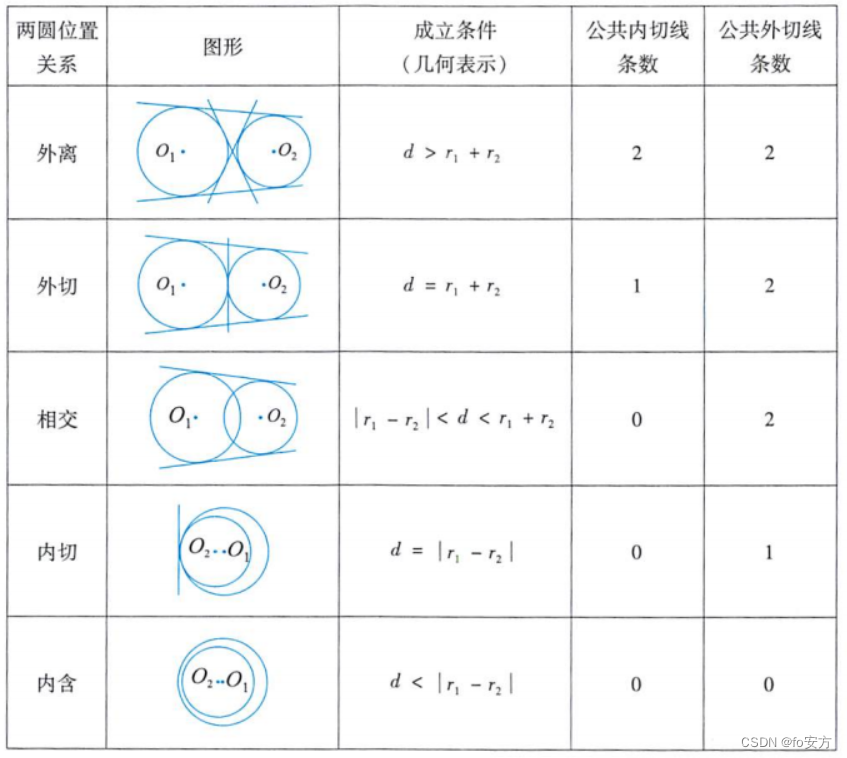
圆与圆的位置关系:圆 O 1 O_1 O1: ( x − x 1 ) 2 + ( y − y 1 ) 2 = r 1 2 (x-x_1)^2+(y-y_1)^2=r_1^2 (x−x1)2+(y−y1)2=r12;圆 O 2 O_2 O2: ( x − x 2 ) 2 + ( y − y 2 ) 2 = r 2 2 (x-x_2)^2+(y-y_2)^2=r_2^2 (x−x2)2+(y−y2)2=r22(不妨 r 1 > r 2 r_1>r_2 r1>r2);d为圆心 ( x 1 , y 1 ) (x_1,y_1) (x1,y1)与 ( x 2 , y 2 ) (x_2,y_2) (x2,y2)的圆心距。
两圆位置关系→公共内切线条数→公共外切线条数:
外离→2→2;外切→1→2;相交→0→2;内切→0→1;内含→0→0。
——图像——
图像的判断
直线过象限题:
两条直线的判断:①若方程 A x 2 + B x y + C y 2 + D x + E y + F = 0 Ax^2+Bxy+Cy^2+Dx+Ey+F=0 Ax2+Bxy+Cy2+Dx+Ey+F=0所表示的图像是两条直线,则可利用双十字相乘法化为 ( A 1 x + B 1 y + C 1 ) ( A 2 x + B 2 y + C 2 ) = 0 (A_1x+B_1y+C_1)(A_2x+B_2y+C_2)=0 (A1x+B1y+C1)(A2x+B2y+C2)=0的形式。② ∣ a x + b y ∣ = c |ax+by|=c ∣ax+by∣=c可化简为 a x + b y = ± c ax+by=±c ax+by=±c,图像是两条关于原点对称的平行直线。
圆的判断:方程 x 2 + y 2 + D x + E y + F = 0 x^2+y^2+Dx+Ey+F=0 x2+y2+Dx+Ey+F=0表示圆的前提为 D 2 + E 2 − 4 F > 0 D^2+E^2-4F>0 D2+E2−4F>0
半圆的判断:若圆的方程为 ( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 (x−a)2+(y−b)2=r2,则
①右半圆的方程为 ( x − a ) 2 + ( y − b ) 2 = r 2 ( x ≥ a ) (x-a)^2+(y-b)^2=r^2(x≥a) (x−a)2+(y−b)2=r2(x≥a)或者 x = a + r 2 − ( y − b ) 2 x=a+\sqrt{r^2-(y-b)^2} x=a+r2−(y−b)2;
②左半圆的方程为 ( x − a ) 2 + ( y − b ) 2 = r 2 ( x ≤ a ) (x-a)^2+(y-b)^2=r^2(x≤a) (x−a)2+(y−b)2=r2(x≤a)或者 x = a − r 2 − ( y − b ) 2 x=a-\sqrt{r^2-(y-b)^2} x=a−r2−(y−b)2;
③上半圆的方程为 ( x − a ) 2 + ( y − b ) 2 = r 2 ( y ≥ b ) (x-a)^2+(y-b)^2=r^2(y≥b) (x−a)2+(y−b)2=r2(y≥b)或者 y = b + r 2 − ( x − a ) 2 y=b+\sqrt{r^2-(x-a)^2} y=b+r2−(x−a)2;
④下半圆的方程为 ( x − a ) 2 + ( y − b ) 2 = r 2 ( y ≤ b ) (x-a)^2+(y-b)^2=r^2(y≤b) (x−a)2+(y−b)2=r2(y≤b)或者 y = b − r 2 − ( x − a ) 2 y=b-\sqrt{r^2-(x-a)^2} y=b−r2−(x−a)2;
四边形的判断:若 ∣ A x − a ∣ + ∣ B y − b ∣ = C |Ax-a|+|By-b|=C ∣Ax−a∣+∣By−b∣=C,则当 A = B A=B A=B时,函数的图像所围成的图形是正方形;当 A ≠ B A≠B A=B时,函数的图像所围成的图形是菱形;无论是正方形还是菱形,面积均为 S = 2 C 2 A B S=\frac{2C^2}{AB} S=AB2C2; ∣ x y ∣ + a b = a ∣ x ∣ + b ∣ y ∣ |xy|+ab=a|x|+b|y| ∣xy∣+ab=a∣x∣+b∣y∣表示 x = ± b , y = ± a x=±b,y=±a x=±b,y=±a的四条直线所围成的矩形,面积为 S = 4 ∣ a b ∣ S=4|ab| S=4∣ab∣。当 a = b a=b a=b时,直线所围成的图形是正方形,面积为 S = 4 a 2 S=4a^2 S=4a2。
——对称——
点关于直线的对称:
点P( x 1 , y 1 x_1,y_1 x1,y1)关于直线l: a x + b y + c = 0 ax+by+c=0 ax+by+c=0的对称点Q的坐标为( x 2 , y 2 x_2,y_2 x2,y2),
方法一:满足两个条件:线段PQ与直线 l l l垂直,即线段PQ的斜率与直线l的斜率之积为 − 1 -1 −1;线段PQ的中点在直线 l l l上。因此Q的坐标可由以下方程组求得:
y 1 = { y 2 − y 1 x 2 − x 1 × ( − a b ) = − 1 a × x 1 + x 2 2 + b × y 1 + y 2 2 + c = 0 y_1 = \begin{cases} \frac{y_2-y_1}{x_2-x_1}×(-\frac{a}{b})=-1 \\ a×\frac{x_1+x_2}{2}+b×\frac{y_1+y_2}{2}+c=0 \end{cases} y1={x2−x1y2−y1×(−ba)=−1a×2x1+x2+b×2y1+y2+c=0——【两点连线的斜率×对称直线的斜率=-1且两点的中点在对称直线上】
方法二: x 2 = x 1 − 2 A A x 1 + B y 1 + C A 2 + B 2 x_2=x_1-2A\frac{Ax_1+By_1+C}{A^2+B^2} x2=x1−2AA2+B2Ax1+By1+C, y 2 = y 1 − 2 B A x 1 + B y 1 + C A 2 + B 2 y_2=y_1-2B\frac{Ax_1+By_1+C}{A^2+B^2} y2=y1−2BA2+B2Ax1+By1+C
直线关于直线的对称:
(1)平行直线的对称
l 1 / / l l_1//l l1//l,因为 l 1 l_1 l1与 l 2 l_2 l2关于 l l l对称,由对称的性质易知 l 1 / / l 2 l_1//l_2 l1//l2,且 l l l到 l 1 l_1 l1与 l 2 l_2 l2的距离 d 1 d_1 d1与 d 2 d_2 d2相等。
若 l 1 l_1 l1的方程为 a x + b y + c 1 = 0 ax + by +c_1=0 ax+by+c1=0, l l l的方程为 a x + b y + c = 0 ax+by+c =0 ax+by+c=0,则可设 l 2 l_2 l2的方程为 a x + b y + c 2 = 0 ax+by+c_2=0 ax+by+c2=0,根据距离相等得到 l 2 l_2 l2的方程为: a x + b y + ( 2 c − c 1 ) = 0 ax+by+(2c-c_1)=0 ax+by+(2c−c1)=0——【对称轴到两直线的距离相等,得 2 c = c 1 + c 2 2c=c_1+c_2 2c=c1+c2】
(2)相交直线的对称
方法一:由 l 1 ∩ l = P l_1∩l=P l1∩l=P,可求出交点坐标。再找出 l 1 l_1 l1上任意一点(点Р除外)关于 l l l对称的点的坐标(用点关于直线对称的方法),再根据两点式求出直线 l 2 l_2 l2的方程。
方法二:由对称性可知 l 1 l_1 l1到 l l l的角与 l l l到 l 2 l_2 l2的角相等,且 l 2 l_2 l2过 l 1 l_1 l1与 l l l的交点 Р Р Р,由到角公式求出 l 2 l_2 l2的斜率,再求出交点 P P P的坐标后,可由点斜式求得直线 l 2 l_2 l2的方程。
(3)直线关于直线对称的万能公式(此公式适用于平行线,相交线两种情况)
已知对称轴 l 0 l_0 l0: A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0;已知直线 l 1 l_1 l1: a x + b y + c = 0 ax+by+c=0 ax+by+c=0;则对称直线 l 2 l_2 l2为 a x + b y + c A x + B y + C = 2 A a + 2 B b A 2 + B 2 \frac{ax+by+c}{Ax+By+C}=\frac{2Aa+2Bb}{A^2+B^2} Ax+By+Cax+by+c=A2+B22Aa+2Bb
圆关于直线对称:实质是点(圆心)关于直线问题,半径保持不变。
关于特殊直线的对称:已知曲线的方程 f ( x , y ) = 0 f(x,y)=0 f(x,y)=0
对称轴:直线 x + y + c = 0 x+y+c=0 x+y+c=0,对称曲线的方程 f ( − y − c , − x − c ) = 0 f(-y-c,-x-c)=0 f(−y−c,−x−c)=0——【把原式中的x替换为-y-c,把原式中的y替换为-x-c】
对称轴:直线 x − y + c = 0 x-y+c=0 x−y+c=0,对称曲线的方程: f ( y − c , x + c ) = 0 f(y-c,x+c)=0 f(y−c,x+c)=0——【把原式中的x替换为y-c,把原式中的y替换为x+c】
对称轴:x轴(直线y=0),对称曲线的方程: f ( x , − y ) = 0 f(x,-y)=0 f(x,−y)=0——【把原式中的y替换为-y】
对称轴:y轴(直线x=0),对称曲线的方程: f ( − x , y ) = 0 f(-x,y)=0 f(−x,y)=0——【把原式中的x替换为-x】
对称轴:直线 x = a x=a x=a,对称曲线的方程: f ( 2 a − x , y ) = 0 f(2a-x,y)=0 f(2a−x,y)=0——【把原式中的x替换为2a-x】
对称轴:直线 y = b y=b y=b,对称曲线的方程: f ( x , 2 b − y ) = 0 f(x,2b-y)=0 f(x,2b−y)=0——【把原式中的y替换为2b-y】
关于点的对称/中心对称:
点关于点对称:使用中点坐标公式求解
直线关于点对称:使用点到两平行线的距离相等求解——两条直线平行
圆关于点对称:使用中点坐标公式求解
——最值——
斜率型最值:求 y − b x − a \frac{y-b}{x-a} x−ay−b最值:设 k = y − b x − a k=\frac{y-b}{x-a} k=x−ay−b,转化为求定点 ( a , b ) (a,b) (a,b)和动点 ( x , y ) (x,y) (x,y)相连所成直线的斜率范围。
截距型最值:求 a x + b y ax+by ax+by最值:设 a x + b y = c ax+by=c ax+by=c,即 y = − a b + c b y=-\frac{a}{b}+\frac{c}{b} y=−ba+bc,转化为求动直线截距的最值。
两点间距离型最值:求 ( x − a ) 2 + ( y − b ) 2 (x-a)^2+(y-b)^2 (x−a)2+(y−b)2最值:设 ( x − a ) 2 + ( y − b ) 2 = r 2 (x-a)^2+(y-b)^2=r^2 (x−a)2+(y−b)2=r2,此时,要求的式子可看作是圆的半径的平方。由于 d = ( x − a ) 2 + ( y − b ) 2 d=\sqrt{(x-a)^2+(y-b)^2} d=(x−a)2+(y−b)2,故所求式子 ( x − a ) 2 + ( y − b ) 2 (x-a)^2+(y-b)^2 (x−a)2+(y−b)2可转化为求定点 ( a , b ) (a,b) (a,b)到动点 ( x , y ) (x,y) (x,y)的距离的平方。
对称求最值:①同侧求最小(考查形式:已知A、B两点在直线l的同侧,在l上找一点P,使得PA+PB最小;解法:作点A(或点B)关于直线l的对称点 A 1 A_1 A1,连接 A 1 B A_1B A1B,交直线l于点P,则 A 1 B A_1B A1B即为所求的最小值,有 ( P A + P B ) m i n = A 1 B (PA+PB)_{min}=A_1B (PA+PB)min=A1B);②异侧求最大(考查形式:已知A、B两点在直线l异侧,在l上找一点P,使得PA-PB最大;解法:作点A(或点B)关于直线l的对称点 A 1 A_1 A1,连接 A 1 B A_1B A1B,交直线l于点P,则 A 1 B A_1B A1B即为所求的最大值,即 ( P A − P B ) m a x = A 1 B (PA-PB)_{max}=A_1B (PA−PB)max=A1B)
圆心求最值:①求圆上的点到直线距离的最值求出圆心到直线的距离,再根据圆与直线的位置关系,求解。一般是距离加半径是最大值,距离减半径是最小值。②求两圆上的点的距离的最值。求出圆心距,再减半径或加半径即可。
直线相关面积:直线 a x + b y + c = 0 ax+by+c=0 ax+by+c=0与两坐标围成的面积为 S = c 2 ∣ 2 a b ∣ S=\frac{c^2}{|2ab|} S=∣2ab∣c2——【】
( x 0 , y 0 x_0,y_0 x0,y0)是直线 a x + b y + c = 0 ax+by+c=0 ax+by+c=0外的一个点,则它到直线的距离d的计算公式为:
d = a x 0 + b y 0 + c a 2 + b 2 d=\frac{ax_0+by_0+c}{\sqrt{a^2+b^2}} d=a2+b2ax0+by0+c
点到点距离: ∣ A 1 A 2 ∣ = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 |A_1A_2|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} ∣A1A2∣=(x2−x1)2+(y2−y1)2
点到直线距离: d = ∣ A x 0 + B y 0 + C ∣ A 2 + B 2 d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}} d=A2+B2∣Ax0+By0+C∣
平行直线距离: d = ∣ C 1 − C 2 ∣ A 2 + B 2 d=\frac{|C_1-C_2|}{\sqrt{A^2+B^2}} d=A2+B2∣C1−C2∣
“点到直线距离公式” ⇒ \Rightarrow ⇒“两平行直线距离公式”:
d = ∣ A x 0 + B y 0 + C ∣ A 2 + B 2 d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}} d=A2+B2∣Ax0+By0+C∣ ⇒ \Rightarrow ⇒ d = ∣ C 1 − C 2 ∣ A 2 + B 2 d=\frac{|C_1-C_2|}{\sqrt{A^2+B^2}} d=A2+B2∣C1−C2∣
已知对称轴 l 0 l_0 l0: A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0;已知直线 l 1 l_1 l1: a x + b y + c = 0 ax+by+c=0 ax+by+c=0;则对称直线 l 2 l_2 l2为:
a x + b y + c A x + B y + C = 2 A a + 2 B b A 2 + B 2 \frac{ax+by+c}{Ax+By+C}=\frac{2Aa+2Bb}{A^2+B^2} Ax+By+Cax+by+c=A2+B22Aa+2Bb
整体利用目录大纲/记忆宫殿
目录大纲
借鉴各大佬的目录,分为如下:
分类1:平面直角坐标系、直线方程与圆的方程、两点间距离公式与点到直线的距离公式
分类2:平面直角坐标系、点、直线、圆
分类3:位置问题、面积问题、对称问题、最值问题
分类4:六大位置关系、五大对称关系(点关于点,点关于直线,直线关于点,相交直线对称,平行直线对称)、
圆与圆的五种位置关系:外离、外切、相交、内切、内含。
记忆宫殿
学习记忆——宫殿篇——记忆宫殿——地点桩——记忆清朝十二个皇帝
从点出发
通过“点”,从1到无数,逐渐引出知识来,但是只能引出关键字,所以还是要按照这个顺序(从1到无数),放到宫殿来,利用宫殿的物品,勾画出对应精华知识。
一个点:无东西
两个点:中点坐标(算术平均值)、距离公式(勾股定理),对称关系
两点成线→直线:直线方程(斜截,点斜,截距,两点,一般)、位置关系(平行,相交,垂直),
一个点与一条直线(三个点):距离公式,位置关系,对称关系,
一条直线与一条直线(四个点):距离公式(两平行直线(相交无距离)),对称关系,
圆(无数点):圆方程(标准式,一般式)
一个点与一个圆(1+无数点):位置关系,对称关系
一条直线与一个圆(2+无数点):位置关系,对称关系
一个圆与一个圆(无数+无数点):位置关系,对称关系
| 点数 | 对象 | 公式 | 位置 | 对称 | 最值 |
|---|---|---|---|---|---|
| 1个点 | - | - | - | - | - |
| 2个点 | 一个点与一个点;直线 | 中点坐标,两点间距离公式;直线的k,直线的方程 | - | 点关于点对称 | 斜率型,截距型,两点距离型,利用对称、圆心 |
| 3个点 | 一个点与一条线(两点成线) | 点到直线距离公式 | 点关于直线对称;直线关于点对称 | ||
| 4个点 | 一条直线与一条直线 | 平行直线间距离公式 | 重合,平行,相交,垂直 | 直线关于直线对称 | |
| 无数点 | 圆 | 圆方程(标准,一般) | - | - | - |
| 无数+1点 | 一个点与一个圆 | 点在圆内,上,外 | 圆关于点对称 | ||
| 无数+2点 | 一条线与一个圆 | 圆上的点与直线的距离 | 相离,相切,相交 | 圆关于直线对称;曲线关于特殊直线对称 | |
| 无数+无数点 | 一个圆与一个圆 | 外离,外切,相交,内切,内含 |
局部用各种方法
数字编码法
学习记忆——记忆宫殿——编码——数字编码和字母编码——两位数
学习记忆——英语——字母编码
学习记忆——记忆宫殿——编码——数字编码——数字声母
-
特殊角度的正切值

转换图像法
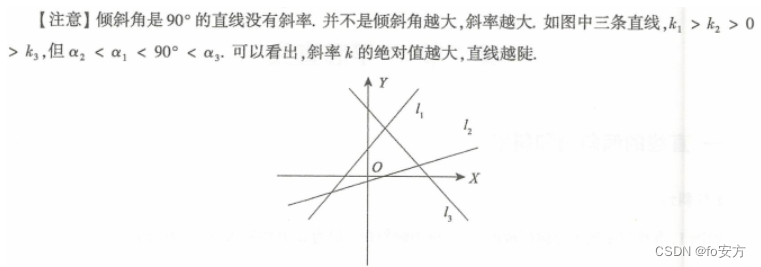
-
两圆位置关系:外离,外切,相交,内切,内含
(1)公共内切线条数:2,1,0,0,0
(2)公共外切线条数:2,2,2,1,0
0呼啦圈;1树,蜡烛;2鹅;

0是D;1是Y;2是Z。
注意,顺序是:从外到内,最最重要的,职业道德的两个呼啦圈。
外离,外切,相交,内切,内含
外:22210,zzzyd,最最重要的
内:21000,zyddd,职业道德的
归类记忆法
数学知识有一个最显著的特点,就是系统性很强。数学知识之间有着内在的联系,我们可以按照它们的特性,恰当归类,使之条理化、系统化,组成一个便于记忆的知识网络。
重点记忆法
抓住一个重点,去推导,去联想。
歌决记忆法
-
平移问题:上加下减,左加右减 ⇒ \Rightarrow ⇒
(1)曲线 y = f ( x ) y=f(x) y=f(x),向上平移α个单位(a>0),方程变为 y = f ( x ) + a y=f(x)+a y=f(x)+a;
(2)曲线 y = f ( x ) y=f(x) y=f(x),向下平移α个单位(a>0),方程变为 y = f ( x ) − a y=f(x)-a y=f(x)−a;
(3)曲线 y = f ( x ) y=f(x) y=f(x),向左平移α个单位(a>0),方程变为 y = f ( x + a ) y=f(x+a) y=f(x+a);
(4)曲线 y = f ( x ) y=f(x) y=f(x),向右平移α个单位(a>0),方程变为 y = f ( x − a ) y=f(x-a) y=f(x−a)。 -
对称求最值:同侧加和求最小值,异侧相减求最大值。
-
垂径定理:有弦先连弦心距,垂直平分用勾股。
转图像记忆法
https://blog.csdn.net/stqer/article/details/132844326
找出规律法
x \sqrt{x} x相关公式
点到点距离: ∣ A 1 A 2 ∣ = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 |A_1A_2|=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2} ∣A1A2∣=(x2−x1)2+(y2−y1)2
点到直线距离: d = ∣ A x 0 + B y 0 + C ∣ A 2 + B 2 d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}} d=A2+B2∣Ax0+By0+C∣
平行直线距离: d = ∣ C 1 − C 2 ∣ A 2 + B 2 d=\frac{|C_1-C_2|}{\sqrt{A^2+B^2}} d=A2+B2∣C1−C2∣
特殊对称

内外切线
直线方程

直线对称万能公式
已知对称轴 l 0 l_0 l0: A x + B y + C = 0 Ax+By+C=0 Ax+By+C=0;已知直线 l 1 l_1 l1: a x + b y + c = 0 ax+by+c=0 ax+by+c=0;则对称直线 l 2 l_2 l2为:
a x + b y + c A x + B y + C = 2 A a + 2 B b A 2 + B 2 \frac{ax+by+c}{Ax+By+C}=\frac{2Aa+2Bb}{A^2+B^2} Ax+By+Cax+by+c=A2+B22Aa+2Bb
直线与直线的位置关系
原理推导法
“点到直线距离公式” ⇒ \Rightarrow ⇒“两平行直线距离公式”:
d = ∣ A x 0 + B y 0 + C ∣ A 2 + B 2 d=\frac{|Ax_0+By_0+C|}{\sqrt{A^2+B^2}} d=A2+B2∣Ax0+By0+C∣ ⇒ \Rightarrow ⇒ d = ∣ C 1 − C 2 ∣ A 2 + B 2 d=\frac{|C_1-C_2|}{\sqrt{A^2+B^2}} d=A2+B2∣C1−C2∣
点
两点中点坐标公式
两点中点坐标公式可以看成是两点坐标的算术平均值。
两点距离公式
两点距离公式是根据平面几何的勾股定理推导出的。
点到直线距离公式
两平行直线的距离

直线关于点的对称

可视化法
管理类联考——数学——可视化篇——代数即几何

这篇关于管理类联考——数学——汇总篇——知识点突破——几何——解析几何——记忆的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!







