第二类专题
Light OJ 1236 Race 第二类斯特林数
第二类斯特林数 n 匹马 分成1 2 3... n组 每一组就是相同排名 没有先后 然后组与组之间是有顺序的 在乘以组数的阶乘 #include <cstdio>#include <cstring>using namespace std;int dp[1010][1010];int a[1010];int main(){a[0] = 1;dp[0][0] = 1;for(int
组合数学几类特殊的数,斯特林第一类数,斯特林第二类数,贝尔数
贝尔数 定义: Bn是基数为n的集合的划分方法的数目。集合S的一个划分是定义为S的两两不相交的非空子集的族,它们的并是S。例如B3 = 5因为3个元素的集合{a, b, c}有5种不同的划分方法: {{a}, {b}, {c}}, {{a}, {b, c}}, {{b}, {a, c}}, {{c}, {a, b}}, {{a, b, c}}。 B0是1,因为空集正好有1种划分方法
UVA 10844 - Bloques (第二类斯特灵数)
UVA 10844 - Bloques 题目链接 题意:给定n个数字,问这n个数字能分成子集分成有几种分法 思路:一开始先想了个状态,dp[i][j]表示放i个数字,分成j个集合的方案,那么转移为,从dp[i - 1][j - 1]在多一个集合,和从dp[i - 1][j]有j个位置放,那么转移方程为dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j] *
自然数幂和 拉格朗日插值法和第二类斯特林数法
写在这里,目的是在以后需要看的时候不用再去网上抄(划掉) 求 s ( n ) = ∑ i = 1 n i k 求s(n)=\sum_{i=1}^n i^k 求s(n)=i=1∑nik 拉格朗日插值法 给定若干个点值,(x0,y0),(x1,y1),(xn,yn),它们的差值多项式 L ( x ) = ∑ i = 0 n y i ∗ ∏ j ≠ i x − x j x i − x j L(
Vision_MATH_球盒问题+第二类Stirling数
///定义: /* 排列组合解决球盒的八大问题,其中用到排列组合公式和第二类斯特林公式 */ ///代码: /***name:第二类斯特林数(第二类Stirling数)**function:解决求不同盒同等问题**公式: S(r, c) = S(r-1,c-1) + c * S(r-1, c)*/#include <iostream>#inclu
格林公式(二维中第二类曲面与第二类曲线曲线互相转换)
第二类曲面与第二类曲线曲线互相转换 设闭区域D由光滑曲线L围成,若P(x,y),Q(x,y)在D上有一阶连续偏导数,则有 其中,L是D的取正向的边界曲线(即沿直线方向前进,左边是D,右边不属于D
hdu2512 第二类斯特林数
题意: 给出n个卡,求这些卡放在一个包里面的方法数 + 放在两个包的方法数 + 放在三个包的方法数 。。。。放在n个包的方法数 的总和 题解: 模板题 第二类斯特拉数 将p个物体排成k个非空集合排列的方法数。s(p,0)=0 ,p>=1 ;s(p,p)=1 ,p>=0。 递推式:s(p,k)=k*s(p-1,k)+s(p-1,k-1) ,1<=k<=p-1
[ACM] SDUT 2883 Hearthstone II (第二类Stiring数)
Hearthstone II Time Limit: 2000ms Memory limit: 65536K 有疑问?点这里^_^ 题目描述 The new season has begun, you have n competitions and m well prepared decks during the new season. Each comp
数据的创建、调用、修改、删除存储过程,以及第一类丢失更新(回滚丢失)和 第二类丢失更新(覆盖丢失/两次更新问题)
数据的创建存储过程、调用存储过程、修改存储过程、删除存储过程,以及第一类丢失更新(回滚丢失)和 第二类丢失更新(覆盖丢失/两次更新问题) 文章目录 一、创建存储的语法二、调用存储过程三、修改存储过程四、删除存储过程五、**第一类丢失更新**(回滚丢失)六、**第二类丢失更新**(覆盖丢失/两次更新问题) 提示:以下是本篇文章正文内容,下面案例可供参考 一、创建存储的语
对坐标的曲面积分@第二类曲面积分
文章目录 abstract曲面基本概念双侧曲面有向曲面曲面区域投影平面区域投影 对坐标的曲面积分流向曲面一侧的流量简单情形 一般情形小结 对坐标的曲面积分其他定义第二类曲面积分的存在性并写和简写流量用第二类曲面积分描述 性质对坐标的曲面积分的计算公式的其他形式应用例例 abstract 对坐标的曲面积分@第二类曲面积分 曲面基本概念 双侧曲面 通常,曲面是双侧的,例如
对坐标的曲面积分@第二类曲面积分
文章目录 abstract曲面基本概念双侧曲面有向曲面曲面区域投影平面区域投影 对坐标的曲面积分流向曲面一侧的流量简单情形 一般情形小结 对坐标的曲面积分其他定义第二类曲面积分的存在性并写和简写流量用第二类曲面积分描述 性质对坐标的曲面积分的计算公式的其他形式应用例例 abstract 对坐标的曲面积分@第二类曲面积分 曲面基本概念 双侧曲面 通常,曲面是双侧的,例如
11.21假设检验,第一第二类错误
两类错误 做假设的时候,首选假设都是已知的参数。 备选假设是不确定的。 要验证的是已知的可能的参数,也就是说是在这样一组数据下的分布,的概率,是不是落在拒绝域里,如果落在拒绝域里就说明当下的假设不成立,选取备用假设。 即验证的时候,用的分布的参数都是当下的参数 第一类错误就是检验假设是正确的,然后落在检验假设拒绝域里的概率; 算这个概率,就是要依据假设的分布参数。这个概率就是显著性
自然数幂和——第一类Stirling数和第二类Stirling数
第一类Stirling数 首先设 $$S_k(n)=\sum_{i=0}^ni^k$$ 根据第一类斯特林数的定义(P是排列数,C是组合数,s是Stirling) $$C_n^k={P_n^k\over k!}={\sum_{i=0}^k(-1)^{i+k}s(k,i)n^i\over k!}$$ 变形得 $$ n^k ={\sum_{i=0}^{k-1}(-1)^{i+k}s(k,i)n^i}-
学习心得——第一类错误、第二类错误、统计功效
一、什么是第一类错误、第二类错误、统计功效 在某个文艺小清新网站上,有一则作者不可考的略黄略暴力的故事很好地阐述了这几个概念:话说N年过去了,某位性别不明的地球统治者决定要消灭地球上的男人们。但是怎样找到地球上所有的男人并把他们都消灭呢?这位统治者开发出了一种自动判别武器——如果胸小于A罩杯,则杀无赦;如果等于或大于A罩杯,则放过。 如果用统计学的语言来说
操作系统学习——第一类R/W问题和第二类R/W问题
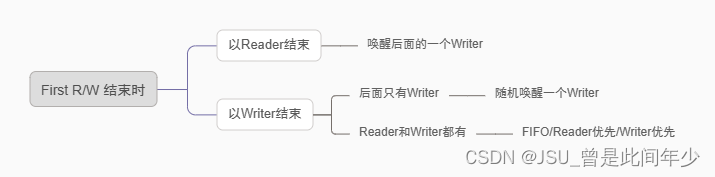
一、First Reader/Writer问题 访问时 结束时 这里因为在第一类读写问题里面Reader可以同时操作,所以在最后一个Reader结束的时刻一定没有其他Reader了 二、Second Reader/Writer问题 第二类问题遵循Writer优先原则,只要存在Writer操作就执行读操作
[LuoguP1829]Crash的文明表格(二次扫描与换根+第二类斯特林数)
Solution: 由于\[ x^m = \sum_{i=0}^m{~m~\choose i}{~x~\brace i}i! \] 将所求的式子化成这样,挖掘其性质,考虑是否能从儿子转移(或利用以求得信息)。\[ \begin{aligned} S(u) &= \sum_{i=1}^ndis(u,i)^k\\ &= \sum_{i=1}^n\sum_{j=0}^k{dis(u, i)
第一类第二类斯特林数学习笔记
第一类斯特林数 p p p个不同人围着 k k k个不同圆桌坐,要求每桌非空,方案数即为 S ( p , k ) S(p,k) S(p,k) 递推 边界 S ( p , p ) = 1 ( p > = 0 ) , S ( p , 0 ) = 0 ( p > = 1 ) S(p,p)=1(p>=0),S(p,0)=0(p>=1) S(p,p)=1(p>=0),S(p,0)=0(p>=1)
hdu 7095 Add or Multiply 1 第二类Stirling数
https://acm.hdu.edu.cn/showproblem.php?pid=7095 给出若干个加法和乘法的操作次数,问有多少个本质不同的操作序列 比如说如果有两个加法和一个乘法,那么得到的操作序列可以是下面的几种 1 ◯ ( ( x + a 1 ) + a 2 ) × a 3 2 ◯ ( ( x + a 1 ) × a 3 ) + a 2 3 ◯ ( ( x + a 2 ) + a



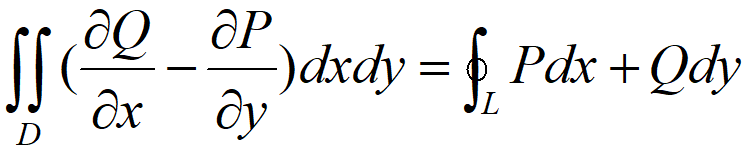
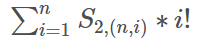




![[LuoguP1829]Crash的文明表格(二次扫描与换根+第二类斯特林数)](https://i.loli.net/2019/08/31/N6DbcXtPal7yQrB.png)