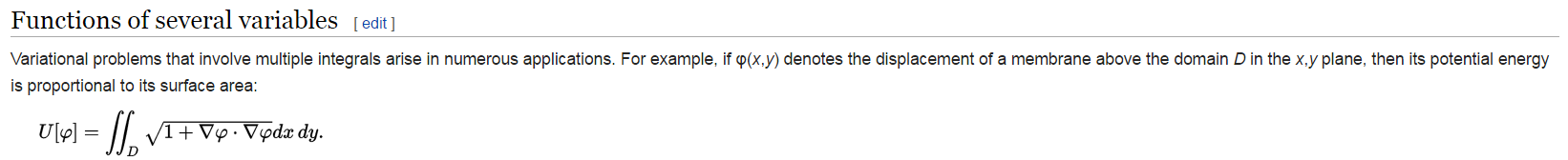第二类曲面积分

本文主要是介绍第二类曲面积分，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

先看高数曲面积分的定义

推导下如何将曲面上的面元投影到xOy平面上, 曲面$z-z(x,y)=0$ 的法向量为$(-z_x, -z_y, 1)$, 单位化后与xOy平面的法向量$(0,0,1)$相乘得到$cos \theta = 1 / \sqrt{1+z_x^2 + z_y^2}$

$dxdy = cos \theta dS$

得证

再看Calculus of variations
https://en.wikipedia.org/wiki/Calculus_of_variations

其中找两点间, 弧长最短的函数$y=f(x)$, 其中这两点可以看成边界条件

对于面积来讲, 找出一个满足边界条件且面积最小的函数$\varphi = \varphi(x,y)$

这里$U[\varphi]$指函数$\varphi$的面积, 注意这里他用的$\nabla \varphi \cdot \nabla \varphi = (\varphi_x, \varphi_y) \cdot (\varphi_x, \varphi_y)= \varphi_x^2 + \varphi_y^2$
这种写法跟我们高数里的写法一样了

然后再看

推导过程如下:

由于是差值,那么表示为$\iint_D (\sqrt{1+\nabla \varphi\cdot \nabla \varphi}-1)dxdy$

然后分子分母同时除以 $(\sqrt{1+\nabla \varphi\cdot \nabla \varphi}+1)$,则结果为

$$\frac{\iint_D \nabla \varphi\cdot \nabla \varphi dxdy}{\sqrt{1+\nabla \varphi\cdot \nabla \varphi}+1}$$

由于微小变化,所以$\sqrt{1+\nabla \varphi\cdot \nabla \varphi}+1 = 2$ 得证

这篇关于第二类曲面积分的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---