皇后专题

题目1254：N皇后问题

题目1254：N皇后问题时间限制：1 秒内存限制：128 兆特殊判题：否题目描述： N皇后问题，即在N*N的方格棋盘内放置了N个皇后，使得它们不相互攻击（即任意2个皇后不允许处在同一排，同一列，也不允许处在同一斜线上。因为皇后可以直走，横走和斜走如下图)。你的任务是，对于给定的N，求出有多少种合法的放置方法。输出N皇后问题所有不同的摆放情况个数。输入

代码训练营 Day26 | 47.排序II | 51. N-皇后 |

47.排序II 1.跟46题一样只不过加一个树层去重 class Solution(object):def backtracking(self,nums,path,result,used):# recursion stopif len(path) == len(nums):# collect our setresult.append(path[:])return for i in range(

JAVA学习-练习试用Java实现“N皇后 II”

问题： n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。给定一个整数 n ，返回 n 皇后问题不同的解决方案的数量。示例 1：输入：n = 4 输出：2 解释：如上图所示，4 皇后问题存在两个不同的解法。示例 2：输入：n = 1 输出：1 提示： 1 <= n <= 9 皇后彼此不能相互攻击，也就是说：任何两个皇后都不能处于同

笔试，牛客.kotori和n皇后，牛客.AOE还是单体

目录牛客.kotori和n皇后编辑牛客.AOE还是单体牛客.kotori和n皇后想起来，我之前还写过n皇后的题，但是这个我开始只能想到暴力解法判断是不是斜对角线，联想y=x+b和y=-x+b,假如在一条线上，那么他们的x和y会对应成比例，这个扫描+判断是一个O(n^2)的操作。 import java.util.*; import java.io.*;//

代码随想录算法训练营第二十五天| 491.递增子序列 46.全排列 47.全排列 II 51.N皇后

目录一、LeetCode 491.递增子序列思路：C++代码二、LeetCode 46.全排列思路C++代码三、LeetCode 47.全排列 II思路C++代码四、LeetCode 51.N皇后思路C++代码总结一、LeetCode 491.递增子序列题目链接：LeetCode 491.递增子序列文章讲解：代码随想录视频讲解：回溯算法精讲，树层去重与树

分书和八皇后问题

1.分数问题：若干个人如何都拿到自己喜欢的书 #include<iostream>#include<iomanip>using namespace std;int Num; //方案数int take[5]; //5本书分别给谁(用户编号)bool assigned[5]; //5本书是否已分配int like[5][5]={{0,0,1,1,0},{1,1,0,0,1},

回溯法-n皇后

N皇后问题问题定义棋盘: 一个n×n的网格。皇后: 一种特殊棋子，可以攻击同一行、同一列或两条对角线上的任何棋子。目标: 在棋盘上放置n个皇后，使得它们之间没有任何一个能够攻击到对方。问题难点确保皇后之间不在同一行或列。避免皇后在对角线上相互攻击。题目分析问题概述在n×n的棋盘上放置n个皇后，要求它们互不攻击。我们使用一个一维数组来存储皇后的坐标。坐标存储使

八皇后问题回溯解法

/****************************************************************************************************************///八皇后问题的求解:使用回溯法#include <stdio.h>#include <math.h>#define N 8int count = 0

HDU2553 N皇后问题

大致题意：在N*N的棋盘上摆放N个皇后，注意是正好N个皇后二不是小于N，使横竖左右均没有对应的皇后，完成一次求解。统计这样的次数。大致思路：如果做过Fire Net （http://acm.hdu.edu.cn/showproblem.php?pid=1045）的话会很自然想到建立一个10 * 10 的二维数组来保存这样的棋盘，每次放置一个棋子并且判断是否可以放置，如果可以放置则进行下一次的搜

【LeetCode】N-Queens II 【九度】题目1254：N皇后问题

N-Queens II Total Accepted: 2737 Total Submissions: 10408 My Submissions Follow up for N-Queens problem. Now, instead outputting board configurations, return the total number of distinct solutions.

回溯法求解N皇后问题及其时间复杂度分析

回溯法求解N皇后问题及其时间复杂度分析一、回溯法简介1. 什么是回溯法？2. 回溯法的时间复杂度分析蒙特卡罗方法蒙特卡罗方法在回溯法求解时间复杂度中的应用二、回溯法求解N皇后问题1. 回溯法求解N皇后问题的过程2. 回溯法求解N皇后问题的时间复杂度2.1 求解时的效率分析回溯法进行效率分析的代码 2.2 时间复杂度分析一、回溯法简介 1. 什么是回溯法？相信"

遗传算法与深度学习实战（7）——使用遗传算法解决N皇后问题

遗传算法与深度学习实战（7）——使用遗传算法解决N皇后问题 0. 前言1. N 皇后问题2. 解的表示3. 遗传算法解决 N 皇后问题小结系列链接 0. 前言进化算法 (Evolutionary Algorithm, EA) 和遗传算法 (Genetic Algorithms, GA) 已成功解决了许多复杂的设计和布局问题，部分原因是它们采用了受控随机元素的搜索。这通常使得使

LeetCode.51N皇后详解

问题描述按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。 n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。给你一个整数 n ，返回所有不同的 n 皇后问题的解决方案。每一种解法包含一个不同的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。 n 皇后问题是一个经典的回溯

N皇后问题(深搜板子题)

N N N皇后问题(以洛谷P1219为例) 在 n × n n\times n n×n大小的棋盘上给出 n n n个皇后，寻找使得所有皇后不同处一行、一列或一条斜线上的摆放方案总数。本题难点在于考虑剪枝条件：对广度进行剪枝(列)对副对角线进行剪枝： i + j i+j i+j对主对角线进行剪枝： i − j + n i-j+n i−j+n(为避免出现负数) #include<bit

回溯法 8皇后

问题太经典，就不描述问题了： public class HuangHou8 {static int n=8;static int tot=0;static int[] C;static int[][] vis=new int[3][16];public static void main(String[] args) {tot=0;C=new int[8];search(0);System.out

回溯法1——八皇后问题

问题：8X8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。思路：回溯法是一种试错方法： 1.先选一个位置试着放置一下，并做“记录”； 2.在每次子问题中进行判定时需要过去的“记录”作为是否可以继续尝试的依据； 3.最后很关键，需要在每次判断结束后将尝试位置进行复位，是为回溯。 #include<stdio.h>#

HDU2553 N皇后问题【回溯法】

N皇后问题 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 9579 Accepted Submission(s): 4314 Problem Description 在N*N的

警惕黑桃皇后组织

好男生一定注意了，别花大量彩礼娶到黑桃皇后组织成员，不值得。渗透已经严重:

HDU--2553 -- N皇后问题

N皇后问题 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 5526 Accepted Submission(s): 2507 Problem Description 在N*N的方格棋盘放置了N个皇后，使得它们不

递归【1】（全排列andN皇后）（排列型回溯）

全排列分治与递归递归是实现分治的一种方法思想思路题目：全排列i 我这样直接输出会多输出一个空行（最后一个\n） #include<stdio.h>using namespace std;const int maxn=10;int an[maxn];int n;bool hash[maxn]={0};int c=0;void pl(int index){

八皇后问题解法及算法分析

什么是八皇后问题八皇后问题，是一个古老而著名的问题，是回溯算法的典型例题。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8X8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。问题解法（C语言），关键看注释，仅供参考 #define N 6 //设置棋盘行列数，既皇后有几个int column[N

【代码随想录】【算法训练营】【第30天】 [322]重新安排行程 [51]N皇后 [37]解数独

前言思路及算法思维，指路代码随想录。题目来自 LeetCode。 day 30，周四，好难，会不了一点~ 题目详情 [322] 重新安排行程题目描述 322 重新安排行程解题思路前提：…… 思路：回溯。重点：……。代码实现 C语言回溯 + 链表自实现超出时间限制！！ /*** Note: The returned array must be mall

代码随想录第三十天打卡|332.重新安排行程， 51. N皇后， 37. 解数独

332.重新安排行程（可跳过）代码随想录 class Solution {public:unordered_map<string,map<string,int>>mp;bool backtracking(int ticketNum,vector<string>&res){if (res.size()==ticketNum+1)return true;for (pair<const str

【代码随想录算法训练Day30】LeetCode 332.重新安排行程、LeetCode 51.N皇后、LeetCode 37.解数独

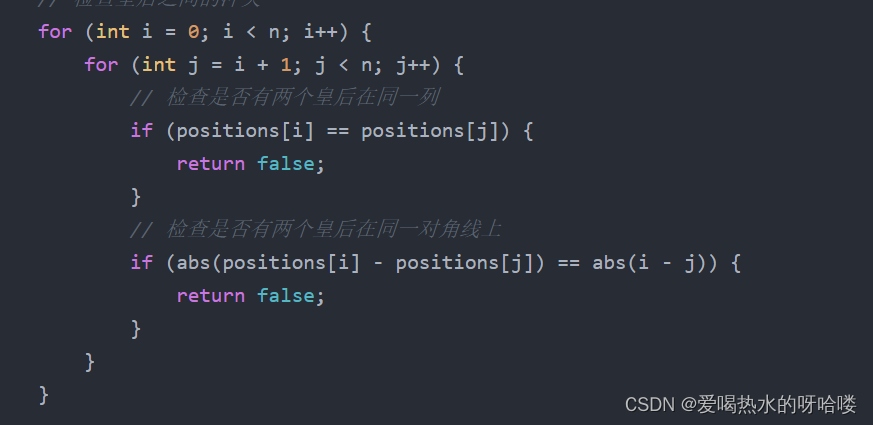
Day30 回溯第六天 LeetCode 332.重新安排行程看了半天也没看懂题，以后再来。 LeetCode 51.N皇后 N皇后题目是回溯算法的经典题目，这道题的难度在思维。我们如何才能正确遍历二维数组，如何确定皇后的摆放位置，这些是本题的难点。在拆分题意后本体其实清晰了很多，我们要做的首先是确定这个格子能不能放皇后，也就是isValid()函数的实现，判断所在行列以及斜线是否有元

算法（十三）回溯算法---N皇后问题

文章目录算法概念经典例子 - N皇后问题什么是N皇后问题？实现思路算法概念回溯算法是类似枚举的深度优先搜索尝试过程，主要是再搜索尝试中寻找问题的解，当发生不满足求解条件时，就会”回溯“返回（也就是递归返回），尝试别的路径求解。经典例子 - N皇后问题什么是N皇后问题？ N皇后问题研究的是：如何将ｎ个皇后放在n * n的棋盘上，并且使皇后彼此之间不能相遇，也就是一

hdu-2553 N皇后问题（深搜 + 状态压缩）

参考大牛博客 http://www.cnblogs.com/gj-Acit/archive/2013/08/04/3236148.html