递归【1】（全排列andN皇后）（排列型回溯）

2024-06-09 04:28
文章标签 递归 皇后 排列 回溯 andn

本文主要是介绍递归【1】（全排列andN皇后）（排列型回溯），希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

全排列

分治与递归

递归是实现分治的一种方法

思想思路

题目：

全排列i

我这样直接输出会多输出一个空行（最后一个\n）

#include<stdio.h>using namespace std;
const int maxn=10;
int an[maxn];
int n;
bool hash[maxn]={0};
int c=0;
void pl(int index)
{if (index>n-1)
{for (int i=0;i<n-1;i++)printf("%d ",an[i]);printf("%d",an[n-1]);printf("\n");return;}		 for(int i=1;i<=n;i++){if (!hash[i]){an[index]=i;hash[i]=1;pl(index+1);c++;hash[i]=0;}}} int main(){scanf("%d",&n);pl(0);}

使用vector存储，在最后一格时不输出

 参考解答

#include <cstdio>
#include <vector>
using namespace std;const int MAXN = 8 + 1;
vector<vector<int> > result;
vector<int> temp;
int n;
bool used[MAXN] = {false};void DFS(int idx) {if (idx == n + 1) {result.push_back(temp);return;}for (int i = 1; i <= n; i++) {if (!used[i]) {temp.push_back(i);used[i] = true;DFS(idx + 1);used[i] = false;temp.pop_back();}}
}int main() {scanf("%d", &n);DFS(1);for (int i = 0; i < result.size(); i++) {for (int j = 0; j < result[i].size(); j++) {printf("%d", result[i][j]);printf(j + 1 < result[i].size() ? " " : "\n");}}return 0;
}

 我也改好了

#include<stdio.h>
#include<vector>
using namespace std;
const int maxn=10;
//int an[maxn];
vector<vector<int> > ans;
vector<int> temp;
int n;
bool hasha[maxn]={0};
int c=0;
void pl(int index)
{if (index>n-1)
{
//for(int j=0;j<temp.size();j++)printf("%d ",temp[j]);ans.push_back(temp);
//	for (int i=0;i<n-1;i++)
//	printf("%d ",an[i]);
//	printf("%d",an[n-1]);
//	 printf("\n");
//	return;}		 for(int i=1;i<=n;i++){if (!hasha[i]){temp.push_back(i);hasha[i]=1;pl(index+1);hasha[i]=0;temp.pop_back();
//			an[index]=i;
//			hash[i]=1;
//			pl(index+1);
//			c++;
//			hash[i]=0;}}} int main(){scanf("%d",&n);pl(0);for(int i=0;i<ans.size();i++){for(int j=0;j<n;j++){printf("%d",ans[i][j]);if (j<n-1)printf(" ");}if(i<ans.size()-1)printf("\n");}}

N皇后

判断8皇后

弃用数组，研究vector的用法搞了半天关于vector的一些菜鸟吐槽-CSDN博客

首先弄明白bool

true是1，false是0

用了二维vector，加上各种边界条件总算搞出来了

可是时间复杂度on3

#include<stdio.h>
#include<vector>
#include<iostream>
using namespace std;
int n=8;
vector<vector<int> > a=vector<vector<int> >(8, vector<int>(8, 0));;
// vector<vector<int> > board = vector<vector<int> >(8, vector<int>(8, 0));int jud(int n,vector<vector<int> > a)//??
{int sum1=0,sum2=0;for(int i=0;i<n;i++){sum1=0;sum2=0;for(int j=0;j<n;j++){sum1+=a[i][j];sum2+=a[j][i];
//行和为1，列和为1//		printf("##??--%d%d%dn%dj%d-\n",i,sum1,sum2,n,j)	;if(a[i][j]==1){for(int k=0;k<n;k++){if(i+j-k<n&&i+j-k>=0&&i+j-k!=i){if(a[i+j-k][j]==a[i][j]){return false;}}if(k+j-i<n&&k+j-i>=0&&k!=i){if(a[k][k+j-i]==a[i][j]){return false;}}}}else if (a[i][j]!=0) 					{return false;}//		printf("#--%d%d%d-\n",i,sum1,sum2)	;}if(sum1!=1||sum2!=1) 					{return false;}}
return true;}
int main()
{
int n1=8;
int ins;
int b[n1][n1];
//printf("%d %d",bool(true),bool(false));for(int i=0;i<n1;i++)for(int j=0;j<n1;j++){scanf("%d",&ins);a[i][j]=ins;}
//printf("%d",jud(n1,a));
if(jud(n1,a))printf("YES"); else printf("NO");
}

事实上答案只用了1-D数组（1的单坐标），并且遍历比我少一半（j>i）即可，减少重复

#include <iostream>
#include <vector>
#include <cmath>using namespace std;bool isValidQueenPlacement(const vector<vector<int>>& board) {int n = board.size();vector<int> positions(n, -1); // positions[i] 表示第 i 行的皇后所在的列// 遍历棋盘，找出所有皇后的位置for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (board[i][j] == 1) {positions[i] = j;}}}// 检查皇后之间的冲突for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {// 检查是否有两个皇后在同一列if (positions[i] == positions[j]) {return false;}// 检查是否有两个皇后在同一对角线上if (abs(positions[i] - positions[j]) == abs(i - j)) {return false;}}}return true;
}int main() {vector<vector<int>> board = vector<vector<int>>(8, vector<int>(8, 0));for (int i = 0; i < 8; i++) {for (int j = 0; j < 8; j++) {cin >> board[i][j];}}cout << (isValidQueenPlacement(board) ? "YES" : "NO") << endl;

判断这里也巧用绝对值

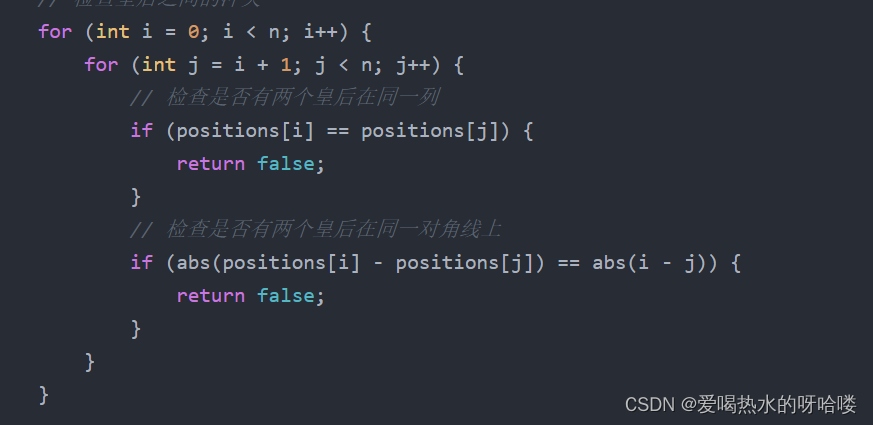
 不过他没有判断皇后同行，似乎是包含在这两个之中了。？

N皇后

·和全排列一样，需要使用hashtable记录某个数字是否被使用

这个错代码看了好多遍了，愣是没发现错在哪

#include <iostream>
#include <vector>
#include <cmath>using namespace std;
const int N=9;
vector<vector<int> > a;
vector<int> temp;
int hashe1[N+2]={0};
void  p(int index,int n)
{if (index==n){printf("?");a.push_back(temp);}for(int i=1;i<n;i++){if(hashe1[i]==0)for (int j=0;j<index;j++){temp.push_back(i);hashe1[i]=1;p(index+1,n);hashe1[i]=0;temp.pop_back();		}}}//}
int main()
{int n=8;
p(0,n);printf("%d",a.size());
}

，对比我自己上次写的全排列，才发现是循环多套了一层。构造排列之后直接判断+pushback还原现场一系列操作即可，但是你却多搞了个j从1-n？

改了还是错

#include <iostream>
#include <vector>
#include <cmath>using namespace std;
const int N=9;
vector<vector<int> > a;
vector<int> temp;
int hashe1[N+2]={0};
void  p(int index,int n)
{if (index==n){printf("?");a.push_back(temp);}for(int i=1;i<n;i++){if(hashe1[i]==0){temp.push_back(i);hashe1[i]=1;p(index+1,n);hashe1[i]=0;temp.pop_back();		}}
}//}
int main()
{int n=8;
p(0,n);printf("%d",a.size());
}

艹！少了个等于！i从1~n，我写的i<n...

#include <iostream>
#include <vector>
#include <cmath>using namespace std;
const int N=9;
vector<vector<int> > a;
vector<int> temp;
int hashe1[N+2]={0};
void  p(int index,int n)
{if (index>n-1){printf("?");a.push_back(temp);}for(int i=1;i<=n;i++){if(hashe1[i]==0){temp.push_back(i);hashe1[i]=1;p(index+1,n);hashe1[i]=0;temp.pop_back();		}}
}//}
int main()
{int n=8;
p(0,n);printf("%d",a.size());
}

 这下至少构造排列部分对了

 然后输出还是0，崩了

#include <iostream>
#include <vector>
#include <cmath>using namespace std;
const int N=9;
vector<vector<int> > a;
vector<int> temp;
int hashe1[N+2]={0};
bool flag=0;
//bool j(vector<int> a)
//{
//	for(int i=0;i<a.size();i++)
//	{//不用判断同行同列，因为造出了是排列
//	for(int j=i+1;i<a.size();j++)
//	{
//		if(abs(a[j]-a[i])==j-i) return false;
//	 } 
//	}
//	return true;
// } 
void  p(int index,int n)
{if (index==n){a.push_back(temp);return;}for(int i=1;i<=n;i++){if(hashe1[i]==0){if(index==0){temp.push_back(i);hashe1[i]=1;p(index+1,n);hashe1[i]=0;temp.pop_back();}else{//printf("?");
//			flag=0;for(int k=0;k<index;k++){//printf("**%d %d %d %d.\n",k,index,temp[k],i);if(abs(i-temp[k])==abs(index-k)) {//printf("*%d %d %d %d.\n",k,index,temp[k],i);flag=1;break;}}if(!flag){//printf("**");temp.push_back(i);hashe1[i]=1;p(index+1,n);hashe1[i]=0;temp.pop_back();}}}}}//}
int main()
{int n=8;
p(0,n);printf("%d",a.size());
}

竟是因为少了个flag归零。蹦

#include <iostream>
#include <vector>
#include <cmath>using namespace std;
const int N=9;
vector<vector<int> > a;
vector<int> temp;
int hashe1[N+2]={0};
bool flag=0;
//bool j(vector<int> a)
//{
//	for(int i=0;i<a.size();i++)
//	{//不用判断同行同列，因为造出了是排列
//	for(int j=i+1;i<a.size();j++)
//	{
//		if(abs(a[j]-a[i])==j-i) return false;
//	 } 
//	}
//	return true;
// } 
void  p(int index,int n)
{if (index==n){a.push_back(temp);return;}for(int i=1;i<=n;i++){if(hashe1[i]==0){if(index==0){temp.push_back(i);hashe1[i]=1;p(index+1,n);hashe1[i]=0;temp.pop_back();}else{//printf("?");flag=0;//这句话害我浪费一个晚上for(int k=0;k<index;k++){//printf("**%d %d %d %d.\n",k,index,temp[k],i);if(abs(i-temp[k])==abs(index-k)) {//printf("*%d %d %d %d.\n",k,index,temp[k],i);flag=1;break;}}if(!flag){//printf("**");temp.push_back(i);hashe1[i]=1;p(index+1,n);hashe1[i]=0;temp.pop_back();}}}}}//}
int main()
{int n=8;
p(0,n);printf("%d",a.size());
}

这篇关于递归【1】（全排列andN皇后）（排列型回溯）的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！


http://www.chinasem.cn/article/1044214。

相关文章

题目1254：N皇后问题

题目1254：N皇后问题

题目1254：N皇后问题 时间限制：1 秒 内存限制：128 兆 特殊判题：否 题目描述： N皇后问题，即在N*N的方格棋盘内放置了N个皇后，使得它们不相互攻击（即任意2个皇后不允许处在同一排，同一列，也不允许处在同一斜线上。因为皇后可以直走，横走和斜走如下图)。 你的任务是，对于给定的N，求出有多少种合法的放置方法。输出N皇后问题所有不同的摆放情况个数。 输入
阅读更多...
PHP字符串全排列

PHP字符串全排列

方法一： $str = 'abc';$a =str_split($str);perm($a, 0, count($a)-1);function perm(&$ar, $k, $m) {if($k == $m){ echo join('',$ar), PHP_EOL;}else {for($i=$k; $i<=$m; $i++) {swap($ar[$k], $ar[$i]);perm($ar
阅读更多...
PHP实现二叉树遍历(非递归方式，栈模拟实现)

PHP实现二叉树遍历(非递归方式，栈模拟实现)

二叉树定义是这样的：一棵非空的二叉树由根结点及左、右子树这三个基本部分组成，根据节点的访问位置不同有三种遍历方式： ① NLR：前序遍历(PreorderTraversal亦称(先序遍历)) ——访问结点的操作发生在遍历其左右子树之前。 ② LNR：中序遍历(InorderTraversal) ——访问结点的操作发生在遍历其左右子树之中(间)。 ③ LRN：后序遍历(PostorderT
阅读更多...
回溯——9.全排列

回溯——9.全排列

力扣题目链接 给定一个 没有重复 数字的序列，返回其所有可能的全排列。 示例: 输入: [1,2,3]输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ] 解题思路 问题建模：题目要求给出一个数组的所有排列组合，属于典型的全排列问题，这可以用回溯法来解决。回溯法通过递归的方式，依次将数组中的每个元素放入排列中，直到生成
阅读更多...
oracle11.2g递归查询（树形结构查询）

oracle11.2g递归查询（树形结构查询）

转自： 一 二 简单语法介绍 一、树型表结构：节点ID 上级ID 节点名称二、公式： select 节点ID,节点名称,levelfrom 表connect by prior 节点ID=上级节点IDstart with 上级节点ID=节点值 oracle官网解说 开发人员：SQL 递归： 在 Oracle Database 11g 第 2 版中查询层次结构数据的快速
阅读更多...
代码训练营 Day26 | 47.排序II | 51. N-皇后 |

代码训练营 Day26 | 47.排序II | 51. N-皇后 |

47.排序II 1.跟46题一样只不过加一个树层去重 class Solution(object):def backtracking(self,nums,path,result,used):# recursion stopif len(path) == len(nums):# collect our setresult.append(path[:])return for i in range(
阅读更多...
Leetcode面试经典150题-128.最长连续序列-递归版本另解

Leetcode面试经典150题-128.最长连续序列-递归版本另解

之前写过一篇这个题的，但是可能代码比较复杂，这回来个简洁版的，这个是递归版本 可以看看之前的版本，两个版本面试用哪个都保过 解法都在代码里，不懂就留言或者私信 class Solution {/**对于之前的解法，我现在提供一共更优的解，但是这种可能会比较难懂一些（思想方面）代码其实是很简洁的，总体思想如下：不需要排序直接把所有数放入map，map的key是当前数字，value是当前数开始的
阅读更多...
风控系统之指标回溯，历史数据重跑

风控系统之指标回溯，历史数据重跑

个人博客：无奈何杨（wnhyang） 个人语雀：wnhyang 共享语雀：在线知识共享 Github：wnhyang - Overview 回顾 默认你已经看过之前那篇风控系统指标计算/特征提取分析与实现01，Redis、Zset、模版方法。 其中已经介绍了如何利用redis的zset结构完成指标计算，为了方便这篇文章的介绍，还是在正式开始本篇之前回顾一下。 时间窗口 zset
阅读更多...
代码随想录刷题day25丨491.递增子序列 ，46.全排列 ，47.全排列 II

代码随想录刷题day25丨491.递增子序列 ，46.全排列 ，47.全排列 II

代码随想录刷题day25丨491.递增子序列 ，46.全排列 ，47.全排列 II 1.题目 1.1递增子序列 题目链接：491. 非递减子序列 - 力扣（LeetCode） 视频讲解：回溯算法精讲，树层去重与树枝去重 | LeetCode：491.递增子序列_哔哩哔哩_bilibili 文档讲解：https://programmercarl.com/0491.%E9%80%92%E
阅读更多...
python 实现第k个字典排列算法

python 实现第k个字典排列算法

第k个字典排列算法介绍 "第k个字典排列"算法通常指的是在给定的字符集合（例如，字符串中的字符）中，找到所有可能排列的第k个排列。这个问题可以通过多种方法解决，但一个常见且高效的方法是使用“下一个排列”算法的变种，或称为“第k个排列”的直接算法。 方法一：使用“下一个排列”的变种 生成所有排列：首先生成所有排列，但显然这种方法对于较大的输入集合是不切实际的，因为它涉及到大量的计算和存储。 排序
阅读更多...

Copyright China编程 23002807@qq.com

沪ICP备2023033072号-2