杯国赛专题
2024年高教杯国赛(D题)数学建模竞赛解题思路|完整代码论文集合
我是Tina表姐,毕业于中国人民大学,对数学建模的热爱让我在这一领域深耕多年。我的建模思路已经帮助了百余位学习者和参赛者在数学建模的道路上取得了显著的进步和成就。现在,我将这份宝贵的经验和知识凝练成一份全面的解题思路与代码论文集合,专为本次赛题设计,旨在帮助您深入理解数学建模的每一个环节。 本次国赛D题可以做如下考虑 本次国赛(五题)完整内容均可以在文章末尾领取! 问题复述 在
2024年高教杯国赛(E题)数学建模竞赛解题思路|完整代码论文集合
我是Tina表姐,毕业于中国人民大学,对数学建模的热爱让我在这一领域深耕多年。我的建模思路已经帮助了百余位学习者和参赛者在数学建模的道路上取得了显著的进步和成就。现在,我将这份宝贵的经验和知识凝练成一份全面的解题思路与代码论文集合,专为本次赛题设计,旨在帮助您深入理解数学建模的每一个环节。 本次国赛E题可以做如下考虑 本次国赛(五题)完整内容均可以在文章末尾领取! 首先问题一对经中路
第15届蓝桥杯国赛JavaA组个人题解
最后两个概率题不会做, 50分没了 博弈论交了暴力, 30%的分 赛后hack了自己1个填空和一个15分的题 算下来应该是66分, 喜提国一最后一名, rank11 A 田字与直线 题目: 9个点按3*3排成矩阵状, 求恰好经过其中2个点的直线个数 答案 过角的: 4个角, 每个2条 不过角: 4个中点, 4条 ans = 12 B 传送阵 题目 42个传送阵, 长度为4
6/1 第十五届蓝桥杯国赛pb组 真题本人答案 仅供参考
6月1日,今天参加了第十五届蓝桥杯国赛,本人打的是pb组,做完回来就把代码复盘了一下。但由于成绩未出,答案仅供参考。 第一题:31 第二题: 没写出来 第三题: dic={}n,m=map(int,input().split())ls=list(map(int,input().split()))for i in range(1,n+1):dic[i]=[]for j
codefun的蓝桥杯国赛之旅
前言 好久没有刷算法了,今天完成了我的蓝桥杯国赛之旅! 总的来说,比赛的过程不是很顺利,只能ac两道题目,好多题都是有思路,但是要么是写不出来,要么是debug不出来,多重背包,回溯+剪枝,图的遍历,都没搞出来,曾经熟悉的算法在不练习之下也会变得生疏! PS:附上一张西科大的图片 蓝桥杯之旅结束了,我的算法之旅还在继续,希望能取得一个好成绩吧, 建议 我认为有比赛一定要去参加,以赛代练促进
2024蓝桥杯国赛C++研究生组游记+个人题解
Day0 开始复习,过了一遍大部分板子 本来打算再学一遍SAM,但是想到去年考了字符串大题今年应该不会再考了吧。。 过了一遍数据结构和图论,就1点了 两点的时候还没睡着,舍友打游戏好像打到2点过。。 Day1 相当困 第一题: 数田字有多少条直线可以只经过两个点,12条 第二题: 求长度42的置换中,周期恰好为2024的置换个数 首先2024=8*11*23,然后8+11+2
【蓝桥杯国赛】二分法
“二分法”的代码模板: (具体参考:查找算法/搜索 | 二分法(python)_python 二分法-CSDN博客) 1. 闭区间:[left, right] def binary_search1(nums, target):left, right = 0, len(nums) - 1 # 闭区间 [left, right]while left <= right: # 区间不为空# 循环
最小质数对-第12届蓝桥杯国赛Python真题解析
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第63讲。 最小质数对,本题是2021年5月29日举办的第12届蓝桥杯青少组Python编程全国总决赛真题编程部分第4题。题目要求给定一个大于2的偶数,编程找出质数差最小的一对,并输出其差值。
最长数字子串-第12届蓝桥杯国赛Python真题解析
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第62讲。 最长数字子串,本题是2021年5月29日举办的第12届蓝桥杯青少组Python编程全国总决赛真题编程部分第3题。题目要求编程对给定的字符串,计算次字符串中最长的数字子串的长度。 先来
Floyd+二分,蓝桥杯国赛2022[环境治理]
一、题目 1、题目描述 2、输入输出 2.1输入 2.2输出 3、原题链接 0环境治理 - 蓝桥云课 (lanqiao.cn) 二、解题报告 1、思路分析 考虑我们治理时间越长,灰尘度和越低,具有单调性 考虑 二分治理天数mid,1~n可以降低与其相连边 mid / n 点的边权 1 ~ mid % n 可以额外降低与其相连边 1点 的边
2023第十四届蓝桥杯国赛C/C++ 大学 A 组 圆上的连线
思路:很显然总的方案数等于挑选偶数点的方案数乘以对应偶数点的连线方案数之和,挑选偶数点的方案数靠组合数得出,偶数点的连线方案数就是个卡特兰数。具体为什么是卡特兰数,可以任选一个点,枚举这个点所连边的位置,这条边把点分为两部分,方案数等于这俩小部分各自方案数的乘积,结合卡特兰数的性质, #include<bits/stdc++.h>using namespace std;#define i
蓝桥杯国赛(最大数字)
前言: 本题是一个典型的回溯问题,en.....题主最开始以为是一个贪心,贪心写的代码只通过了60%qvq 题目描述: 思路: 本题用回溯去查找先对操作1查找再回溯对操作2查找 AC代码: #include <iostream>#include <algorithm>using namespace std;char n[20];int a, b;long long m
第十三届蓝桥杯国赛真题 Java C 组【原卷】
文章目录 发现宝藏试题 A: 斐波那契与 7试题 B: 小蓝做实验试题 C: 取模试题 D: 内存空间试题 E \mathrm{E} E : 斐波那契数组试题 F: 最大公约数试题 G: 交通信号试题 I: 打折试题 J: 宝石收集 发现宝藏 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默,忍不住分享一下给大家。【宝藏入口】。 第十三届蓝桥杯大赛软件赛国赛
2019年第十届蓝桥杯国赛总结(JavaA组)
JavaA组国二,可以报销了~ JA死亡之组可不是盖的,rank12的排名还是拿不到国一啊(只有五个。。 出成绩的一刻波澜不惊,毕竟去年有国一了不慌哈哈哈 不过对我来说这个结果还算意料之外吧,毕竟大三考研狗 这次再也不敢说蓝桥杯水了,十周年十道题分分钟教你做人... 不仅题量大时间紧,题目难度也在向ACM看齐(ACM还让带板子呢。。 先说题目吧,具体记不太清了,有错误欢迎指正 第一题三升序列
第十届蓝桥杯国赛 C++ B组(仅题目)
试题 A: 平方序列 问题描述 小明想找到两个正整数 X 和 Y,满足 2019 < X < Y;20192 , X2 , Y2 组成等差数列。 请你求出在所有可能的解中,X + Y 的最小值是多少? 答案提交 这是一道结果填空的题,你只需要算出结果后提交即可。 本题的结果为一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。 试题 B: 质数拆分 问题描述 将
第十四届蓝桥杯国赛 C++ A 组 E 题——第K小的和(AC)
目录 1. 第K小的和1. 问题描述2. 输入格式3. 输出格式4. 样例输入5. 样例输出6. 评测用例规模与约定7. 原题链接 2. 解题思路3. AC_Code 1. 第K小的和 前置知识点:二分,排序 1. 问题描述 给定两个序列 A , B A, B A,B,长度分别为 n , m n, m n,m。 设另有一个序列 C C C 中包含了 A , B A,
计算阶乘-第11届蓝桥杯国赛Python真题精选
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第34讲。 计算阶乘,本题是2020年10月30日举办的第11届蓝桥杯青少组Python编程国赛编程部分第1题,题目要求计算输入数字的阶乘。 先来看看题目的要求吧。 一.题目说明 提示信息:
第十四届蓝桥杯国赛 C++ B 组 C 题——班级活动(AC)
目录 1. 班级活动1. 问题描述2. 输入格式3. 输出格式4. 样例输入5. 样例输出6. 样例说明7. 评测用例规模与约定8. 原题链接 2. 解题思路3. AC_Code 1. 班级活动 前置知识点:思维,分类讨论 1. 问题描述 小明的老师准备组织一次班级活动。班上一共有 n n n 名 ( n n n 为偶数) 同学,老师想把所有的同学进行分组,每两名同学一组。
2019年第十届蓝桥杯国赛C++B组
文章目录 平方序列质数拆分拼接求值路径计数最优包含排列数解谜游戏第八大奇迹燃烧权杖 平方序列 【问题描述】 小明想找到两个正整数 X 和 Y,满足 • 2019 < X < Y; • 20192, X2, Y2 组成等差数列。 请你求出在所有可能的解中, X + Y 的最小值是多少? 3111 + 3909 = 7020 #include<bits/stdc++.h
电梯用电量-第10届蓝桥杯国赛Python真题精选
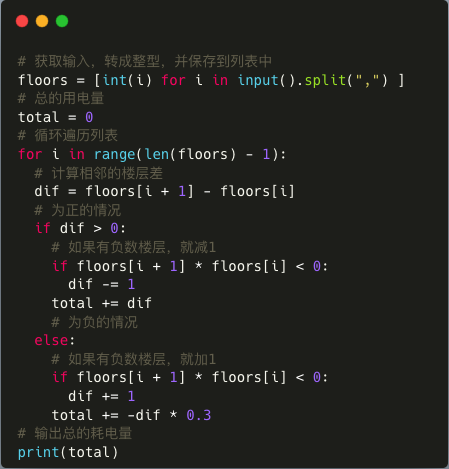
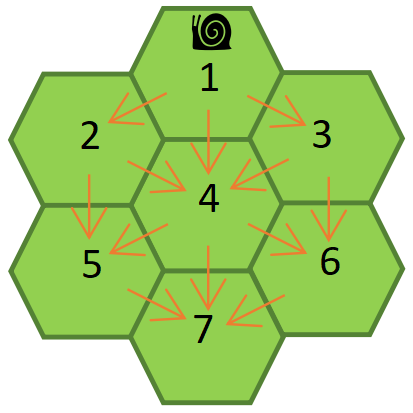
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第8讲。 电梯用电量,本题是2019年5月25日举行的第10届蓝桥杯青少组Python编程国赛真题,题目要求通过输入的某段时间内电梯停过的楼层顺序,编程计算电梯消耗了多少单位电量。 先来看看题目
第十四届蓝桥杯国赛python青少组题目
LQGS14PB01 时间限制: 3000MS 内存限制: 589824KB 题目描述: 编程实现: (注.input()输入函数的括号中不允许添加任何信息) 给定一个字符串S(S长度<100),统计字符串中字母一共有多少个。 例如:S =“1Abb”,其中字母有A,b,b一共有3个。 输入描述 输入一个字符串S(S长度<100) 输出描述 输出一个整数,表示字符串S中字母的个数 样例输入 1Ab
第十三届蓝桥杯国赛JavaB组题解
A. 重合次数 思路: 枚举不同的时刻,判断哪些时刻秒针和分针表示的数字是相同的。这道题坑就坑在:xx:59:59 xx:00:00分针和时。也就是说一个小时会重叠两次。 题目要求是分钟和秒钟的重叠次数,故时钟,分钟,秒钟同时重叠的次数不算(这题还是有点咬文嚼字了,我说怎么比答案多了8次)。 代码: import java.io.BufferedReader;import java.i
2022年第十三届蓝桥杯国赛JavaB组-决赛部分题解
题目与部分参考答案 这题要考虑一下一个小时分针与秒针重合的次数只有59次,没有60次。第x1:59:00~x1:59:59这六十秒里分针和秒针不会重合。 而到x2:00:00时会重合,但是这已经是另一个小时了。 答案:494(502 - 8) import java.util.Scanner;public class Main {public static void main(String
第十届蓝桥杯国赛Scratch编程真题解析:逃不掉的小球
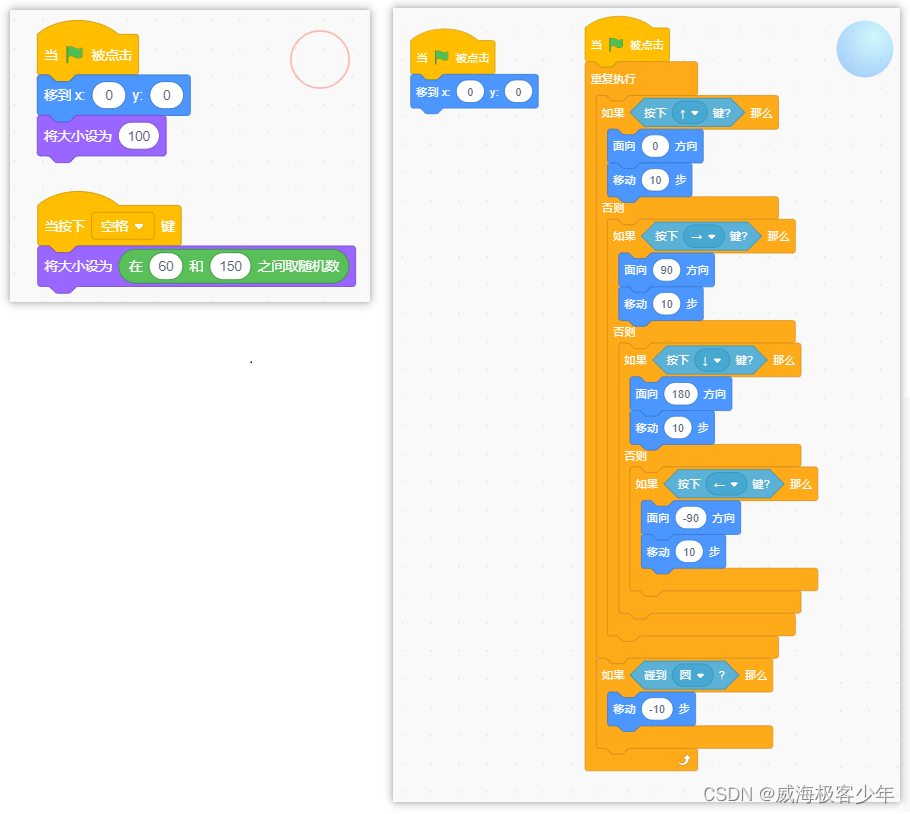
逃不掉的小球 准备工作 从角色库中选择《Ball》小球角色,绘制1个轮廓较粗的红色空心圆。 编程实现 键盘控制小球运动,小球不能越过圆形边缘。 具体要求 圆形和小球都放置在舞台中间,如上图所示。点击绿旗,使用上、下、左、右按键可以控制小球上下左右移动,但在程序未运行时,按下按键则应该不能控制小球移动。小球只能在其圆形范围内移动,允许触碰到边缘,但不能越过边缘。当按下空格键时,小球要回









![Floyd+二分,蓝桥杯国赛2022[环境治理]](https://img-blog.csdnimg.cn/direct/5693c32bb3204e06a1c8504b5fa80596.png)