第十三届蓝桥杯国赛JavaB组题解

A. 重合次数

思路：

枚举不同的时刻，判断哪些时刻秒针和分针表示的数字是相同的。这道题坑就坑在:xx:59:59 xx:00:00分针和时。也就是说一个小时会重叠两次。
题目要求是分钟和秒钟的重叠次数,故时钟,分钟,秒钟同时重叠的次数不算(这题还是有点咬文嚼字了,我说怎么比答案多了8次)。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;public class Main {static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static StreamTokenizer in = new StreamTokenizer(br);public static int nextInt() throws IOException {in.nextToken();return (int) in.nval;}public static void main(String[] args) {// TODO Auto-generated method stubint h = 6, m = 13, s = 22;int cnt = 0;while (h != 14 || m != 36 || s != 20) {if (m == s) cnt++;s++;if (s == 60) {m++;s = 0;}if (m == 60) {h++;m = 0;}}// 减去整点重复System.out.println(cnt - 8);}
}

B. 数数

思路：

这道题本来想通过搜索判断一个数是否可以用12个质因数表示，但是失败了。后来想到可以用试除法分解质因数判断一个数是否可以被分解成12个质因子，虽然最后也跑了一会儿不过作为填空题还是给过了。

代码：

public class Main {static int ans;public static boolean check(int x) {int cnt = 0;for (int i = 2; i <= x / i; i++) {if (x % i == 0) {while (x % i == 0) {x /= i;cnt++;}}}return cnt == 12;}public static void main(String[] args) {// TODO Auto-generated method stub// for (int i = 2333333; i <= 23333333; i++) //     if (check(i)) ans++;System.out.println(25606);}
}

C. 左移右移

思路：

初始的想法是保存每个数的位置，当某个数左移的时候，左边的每个数的位置都+1，右边的数不变；当某个数右移的时候，右边的每个数的位置都-1，左边的数不变，自然而然想到了差分，算出位置后，接着再根据位置输出即可。但是后来想想每次都要求得每个数的位置，复杂度为 $O(N)$，一共有 $M$ 个操作，复杂度就是 $O(NM)$，最大程度会 $4\times 10^{10}$ ，显然会超时，这种做法不可取。

后来想到了用双链表进行求解，每次交换位置的时候要先删除再插入，在插入的时候更新元素的位置。在 $O(N)$ 的复杂度内可以得到正确答案。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;public class Main {static final int N = 400010;static int[] e = new int[N], l = new int[N], r = new int[N], loc = new int[N];static int n, m, idx;static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));public static void insert(int k, int x) {loc[x] = idx;e[idx] = x;l[idx] = k;r[idx] = r[k];l[r[k]] = idx;r[k] = idx++;}public static void remove(int k) {r[l[k]] = r[k];l[r[k]] = l[k];}public static void main(String[] args) throws IOException {// TODO Auto-generated method stubString[] nm = br.readLine().split(" ");n = Integer.parseInt(nm[0]);m = Integer.parseInt(nm[1]);// 0为头节点，1为尾节点l[1] = 0;r[0] = 1;idx = 2;for (int i = 1; i <= n; i++) insert(l[1], i);while (m-- != 0) {String[] ops = br.readLine().split(" ");char op = ops[0].charAt(0);int x = Integer.parseInt(ops[1]);if (op == 'L') {remove(loc[x]);insert(0, x);} else {remove(loc[x]);insert(l[1], x);}}for (int i = r[0]; i != 1; i = r[i]) out.printf("%d ", e[i]);out.flush();}
}

D. 窗口

思路：

定义窗口类，存储相关信息：

static class Window implements Comparable<Window> {int pid, top, left, height, width, priority;Window(int pid, int top, int left, int height, int width, int priority) {this.pid = pid;this.top = top;this.left = left;this.height = height;this.width = width;this.priority = priority;}void move(int ver, int hor) {this.top += ver;this.left += hor;this.priority = ++pri;}void resize(int h, int w) {this.height = h;this.width = w;this.priority = ++pri;}@Overridepublic int compareTo(Window o) {// TODO Auto-generated method stubreturn priority - o.priority;}}

依次处理每个操作，更新窗口信息。接着将窗口按优先级从小到大排序，优先级为0的窗口不予处理。在根据排好序的窗口绘制图形，就能实现优先级较大的窗口处于顶层。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.util.Arrays;
import java.util.HashSet;public class Main {static final int N = 300, M = 100010;static char[][] g = new char[N][N];static Window[] arr = new Window[M];static Window[] wins = new Window[M];static int n, m, k, pri = 0;static class Window implements Comparable<Window> {int pid, top, left, height, width, priority;Window(int pid, int top, int left, int height, int width, int priority) {this.pid = pid;this.top = top;this.left = left;this.height = height;this.width = width;this.priority = priority;}void move(int ver, int hor) {this.top += ver;this.left += hor;this.priority = ++pri;}void resize(int h, int w) {this.height = h;this.width = w;this.priority = ++pri;}@Overridepublic int compareTo(Window o) {// TODO Auto-generated method stubreturn priority - o.priority;}}static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));public static void draw(int x1, int y1, int x2, int y2) {for (int i = x1; i <= x2; i++) for (int j = y1; j <= y2; j++) {if (i < 0 || i >= n || j < 0 || j >= m) continue;if (i == x1 || i == x2) {if (j == y1 || j == y2) g[i][j] = '+';else g[i][j] = '-';} else if (j == y1 || j == y2) g[i][j] = '|';else g[i][j] = ' ';}}public static void main(String[] args) throws IOException {// TODO Auto-generated method stubString[] nm = br.readLine().split(" ");n = Integer.parseInt(nm[0]);m = Integer.parseInt(nm[1]);k = Integer.parseInt(br.readLine());HashSet<Integer> pSet = new HashSet<Integer>();for (int i = 0; i < k; i++) {String[] op = br.readLine().split(" ");int id = Integer.parseInt(op[1]);pSet.add(id);if (op[0].equals("new")) {int t = Integer.parseInt(op[2]);int l = Integer.parseInt(op[3]);int h = Integer.parseInt(op[4]);int w = Integer.parseInt(op[5]);arr[id] = new Window(id, t, l, h, w, ++pri);} else if (op[0].equals("move")) {int ver = Integer.parseInt(op[2]);int hor = Integer.parseInt(op[3]);arr[id].move(ver, hor);} else if (op[0].equals("resize")) {int h = Integer.parseInt(op[2]);int w = Integer.parseInt(op[3]);arr[id].resize(h, w);} else if (op[0].equals("close")) {arr[id].priority = 0;} else {arr[id].priority = ++pri;}}int num = 0;for (Integer id : pSet) {wins[num++] = arr[id];}Arrays.sort(wins, 0, num);for (int i = 0; i < n; i++)for (int j = 0; j < m; j++)g[i][j] = '.';for (int i = 0; i < num; i++) {if (wins[i].priority != 0) {int x1 = wins[i].top;int y1 = wins[i].left;int x2 = x1 + wins[i].height - 1;int y2 = y1 + wins[i].width - 1;draw(x1, y1, x2, y2);}}for (int i = 0; i < n; i++) {for (int j = 0; j < m; j++)out.print(g[i][j]);out.println();}out.flush();  }
}

E. 迷宫

思路：
bfs求最短路，从终点一次bfs可以求得到所有点的最短距离，将所有点的最短距离相加再除以点数即可得到最短距离的数学期望。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Queue;public class Main {static final int N = 2010, M = N * N, inf = 0x3f3f3f3f;static int[] h = new int[M], e = new int[N * 2], ne = new int[N * 2];static int[][] d = new int[N][N];static int[] dx = {-1, 0, 1, 0}, dy = {0, 1, 0, -1};static int n, m, idx;static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static StreamTokenizer in = new StreamTokenizer(br);public static int nextInt() throws IOException {in.nextToken();return (int) in.nval;}public static void add(int a, int b) {e[idx] = b;ne[idx] = h[a];h[a] = idx++;}public static int get(int x, int y) {return x * N + y;}public static void bfs() {for (int i = 0; i <= n; i++)for (int j = 0; j <= n; j++)d[i][j] = inf;Queue<Integer> q = new LinkedList<Integer>();q.offer(n * N + n);d[n][n] = 0;while (!q.isEmpty()) {int v = q.poll();int x = v / N, y = v % N;for (int i = 0; i < 4; i++) {int tx = x + dx[i], ty = y + dy[i];if (tx <= 0 || tx > n || ty <= 0 || ty > n) continue;if (d[tx][ty] > d[x][y] + 1) {d[tx][ty] = d[x][y] + 1;q.offer(tx * N + ty);}}for (int i = h[v]; i != -1; i = ne[i]) {int j = e[i];int tx = j / N, ty = j % N;if (d[tx][ty] > d[x][y] + 1) {d[tx][ty] = d[x][y] + 1;q.offer(tx * N + ty);}}}}public static void main(String[] args) throws IOException {// TODO Auto-generated method stubn = nextInt();m = nextInt();Arrays.fill(h, -1);while (m-- != 0) {int x1 = nextInt();int y1 = nextInt();int x2 = nextInt();int y2 = nextInt();int a = get(x1, y1);int b = get(x2, y2);add(a, b);add(b, a);}bfs();long ans = 0;for (int i = 1; i <= n; i++) for (int j = 1; j <= n; j++) ans += d[i][j];out.printf("%.2f", ans * 1.0 / (n * n));out.flush();}}

F. 小球称重

思路：
思路比较简单，直接上代码吧。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.HashSet;public class Main {static int n, m;static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static StreamTokenizer in = new StreamTokenizer(br);public static int nextInt() throws IOException {in.nextToken();return (int) in.nval;}public static void main(String[] args) throws IOException {// TODO Auto-generated method stubString[] nm = br.readLine().split(" ");n = Integer.parseInt(nm[0]);m = Integer.parseInt(nm[1]);HashSet<String> abnormal = new HashSet<>();HashSet<String> tmp = new HashSet<>();HashSet<String> normal = new HashSet<>();while (m-- != 0) {int k = Integer.parseInt(br.readLine());String[] a = br.readLine().split(" ");String[] b = br.readLine().split(" ");HashSet<String> left = new HashSet<String>();HashSet<String> right = new HashSet<String>();for (int i = 0; i < k; i++) {left.add(a[i]);right.add(b[i]);}char op = br.readLine().charAt(0);if (op == '<') {if (abnormal.isEmpty()) abnormal = left;else {tmp = new HashSet<String>();for (String x : left) {if (abnormal.contains(x)) tmp.add(x);}    abnormal = tmp;}} else if (op == '>') {if (abnormal.isEmpty()) abnormal = right;else {tmp = new HashSet<String>();for (String x : right) {if (abnormal.contains(x)) tmp.add(x);}    abnormal = tmp;}} else {normal.addAll(left);normal.addAll(right);for (String x : left) abnormal.remove(x);for (String x : right) abnormal.remove(x);}  }if (abnormal.isEmpty()) out.println(n - normal.size());else out.println(abnormal.size());out.flush();}}

G. 背包与魔法

思路分析：
本题是01背包问题的变种，限制条件是最多只能使用一次魔法，求所装物品的最大值。由于使用和不使用有两个状态，因此背包需要再开一维状态，我们用0表示没有使用魔法，用1表示使用魔法。状态表示f[i,j,k]所有用前 $i$ 个物品，总体不超过 $j$ ，使用/不适用魔法的价值的最大值。本问题的分析过程大部分与01背包问题相同，区别在于判断是否使用魔法。
当 $j>=k-w[i]$ 时，更新使用魔法的最大值，$$f[i,j,1]=max(f[i,j,1],f[i-1,j-k-w[i],0]+2\ast v[i])$$

下面是使用闫氏DP分析法的分析过程：

值得注意的是，由于本题数据范围太大，需要优化为二维才能过，否则会超时

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;public class Main {static final int N = 2010, M = 10010;static int[][] dp = new int[M][2];static int[] v = new int[N], w = new int[N];static int n, m, k;static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static StreamTokenizer in = new StreamTokenizer(br);public static int nextInt() throws IOException {in.nextToken();return (int) in.nval;}public static void main(String[] args) throws IOException {// TODO Auto-generated method stubn = nextInt();m = nextInt();k = nextInt();for (int i = 1; i <= n; i++) {w[i] = nextInt();v[i] = nextInt();}for (int i = 1; i <= n; i++) {for (int j = m; j >= w[i]; j --) {dp[j][0] = Math.max(dp[j][0], dp[j - w[i]][0] + v[i]);dp[j][1] = Math.max(dp[j][1], dp[j - w[i]][1] + v[i]);if (j >= k + w[i]) dp[j][1] = Math.max(dp[j][1], dp[j - k - w[i]][0] + v[i] * 2);}}out.println(Math.max(dp[m][0], dp[m][1]));out.flush();}}

H. 修路

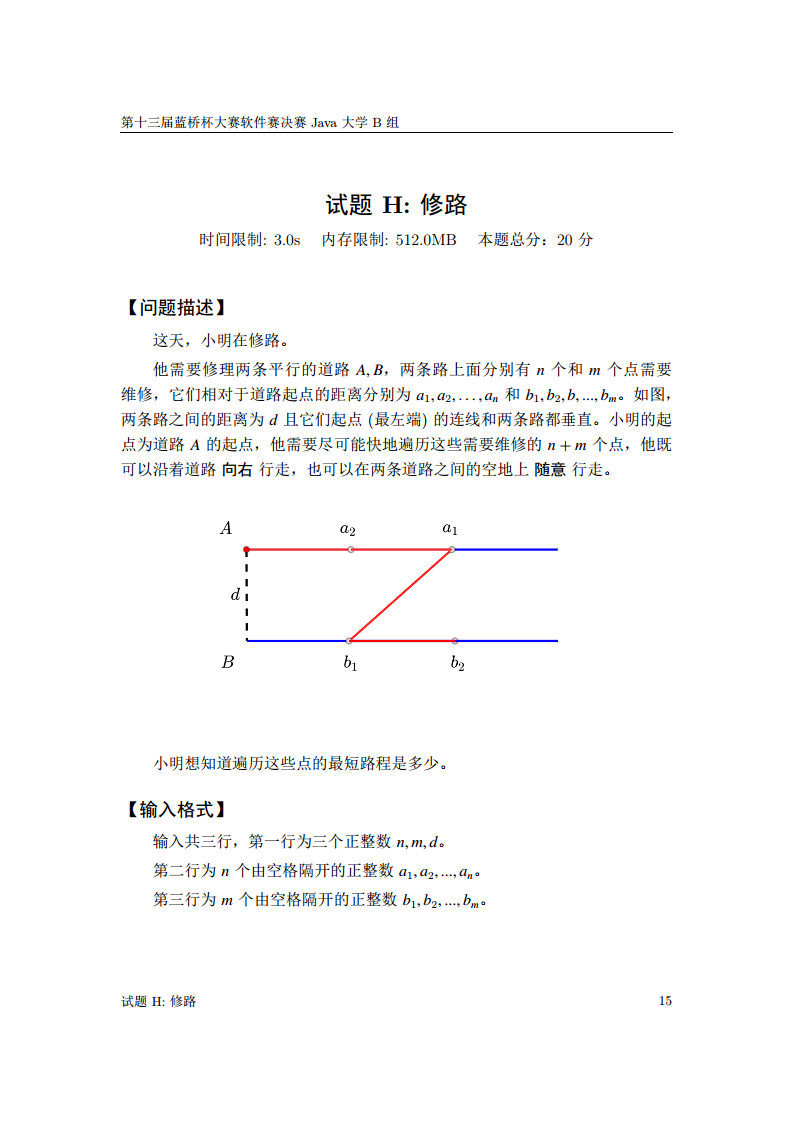
思路：
本题是一个动态规划的题目，可以用闫氏DP分析法分析问题：分析过程如下：

状态 $f(i,j,k)$ 表示所有走过 $a_i$ 、$b_j$ 的所有走法的集合，属性为 $min$。

当 $k=0$ 时，表示当前在道路 $A$ 上；当 $k=1$ 时，表示当前在道路 $B$ 上。

根据 上一个点在 $b_j$ 还是 $a_{i-1}$ 上可以划分状态计算，每一类又有两种情况：在道路 $A$ 上，在道路 $B$ 上，分别取 $min$ 即可。

重点在于初始化，状态转移方程为：
{ f ( i , j , 0 ) = m i n { f ( i − 1 , j , 0 ) + a i − a i − 1 , f ( i − 1 , j , 1 ) + d i s t ( a i , b j ) } f ( i , j , 1 ) = m i n { f ( i , j − 1 , 0 ) + d i s t ( a i , b j ) , f ( i , j − 1 , 1 ) + b j − b j − 1 } \begin{cases} f(i, j,0) = min\{f(i - 1, j, 0) + a_i - a_{i - 1}, f(i - 1, j, 1) + dist(a_i, b_j) \} \\ f(i, j,1) = min\{f(i, j - 1, 0) + dist(a_i, b_j), f(i , j - 1, 1) +b_j - b_{j - 1} \} \\ \end{cases} {f(i,j,0)=min{f(i−1,j,0)+ai​−ai−1​,f(i−1,j,1)+dist(ai​,bj​)}f(i,j,1)=min{f(i,j−1,0)+dist(ai​,bj​),f(i,j−1,1)+bj​−bj−1​}​

通过 $O(NM)$ 的时间复杂度可以求解。

代码：

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.OutputStreamWriter;
import java.io.PrintWriter;
import java.io.StreamTokenizer;
import java.util.Arrays;public class Main {static final int N = 2010;static int[] a = new int[N], b = new int[N];static double[][][] f = new double[N][N][2]; static int n, m, d;static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));static PrintWriter out = new PrintWriter(new OutputStreamWriter(System.out));static StreamTokenizer in = new StreamTokenizer(br);public static int nextInt() throws IOException {in.nextToken();return (int) in.nval;}public static void main(String[] args) throws IOException {// TODO Auto-generated method stubn = nextInt();m = nextInt();d = nextInt();a[0] = b[0] = 0;for (int i = 1; i <= n; i++) a[i] = nextInt();for (int i = 1; i <= m; i++) b[i] = nextInt();Arrays.sort(a, 0, n + 1);Arrays.sort(b, 0, m + 1);for (int i = 1; i <= n; i++) {f[i][0][0] = a[i];f[i][0][1] = 1e9;}f[0][1][0] = 1e9;f[0][1][1] = Math.hypot(d, b[1]);for (int i = 2; i <= m; i++) {f[0][i][0] = 1e9;f[0][i][1] = f[0][i - 1][1] + b[i] - b[i - 1];}for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {// 走到aif[i][j][0] = Math.min(f[i - 1][j][0] + a[i] - a[i - 1], f[i - 1][j][1] + Math.hypot(d, a[i] - b[j]));// 走到bjf[i][j][1] = Math.min(f[i][j - 1][0] + Math.hypot(d, a[i] - b[j]), f[i][j - 1][1] + b[j] - b[j - 1]);}}out.printf("%.2f", Math.min(f[n][m][0], f[n][m][1]));out.flush();}}

I. 围栏

思路：