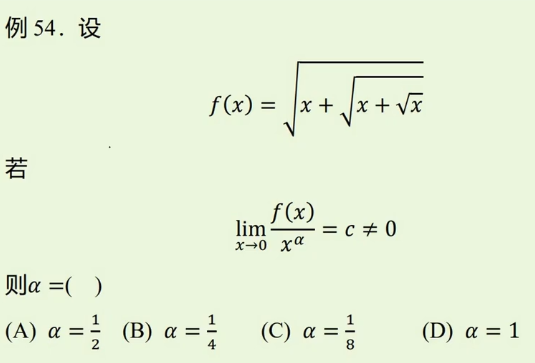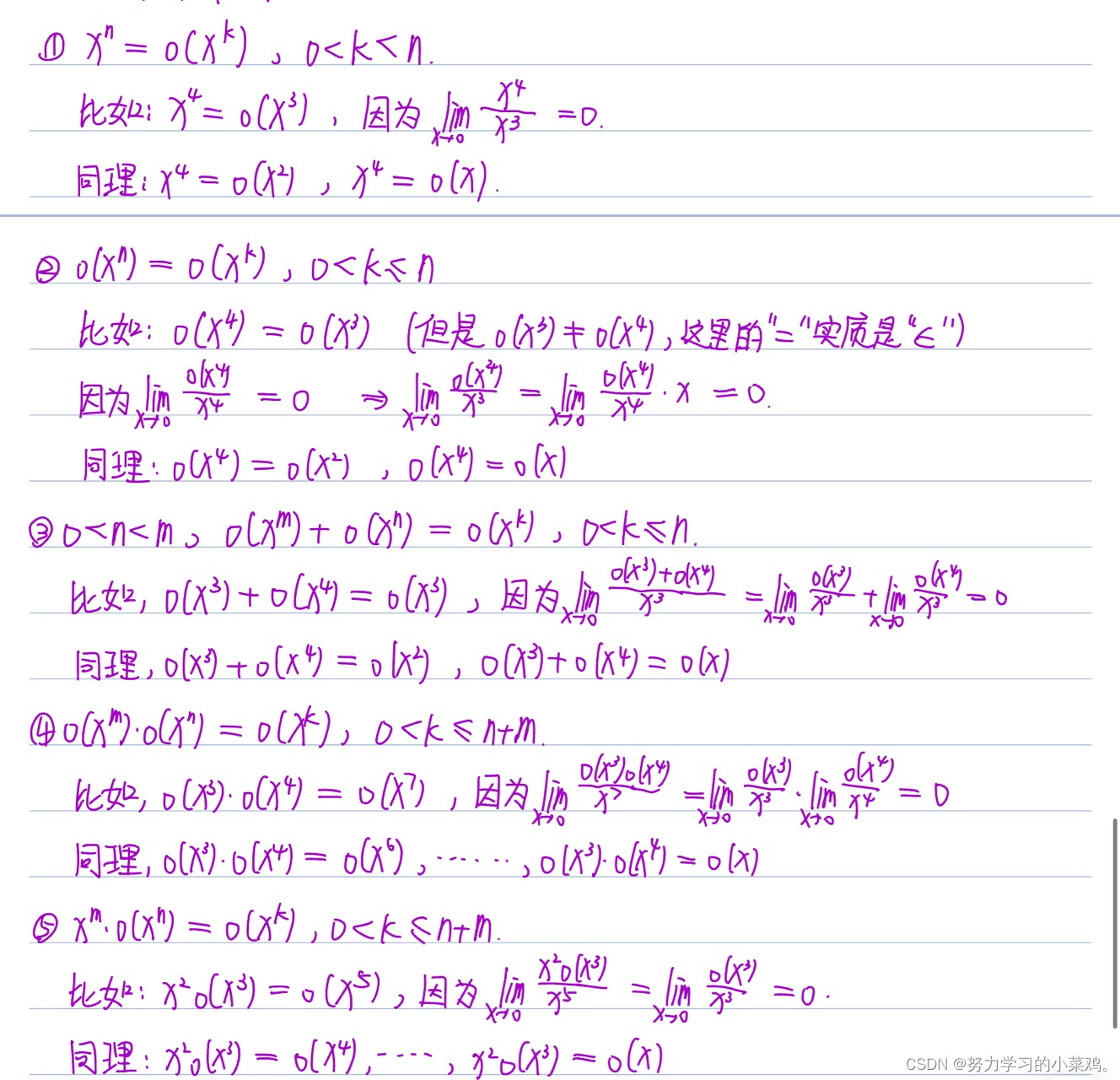无穷小专题
变上限积分无穷小比阶与导数的关系问题
变上限积分无穷小比阶与导数的关系问题 @(微积分) (2004)把 x→0+ x\rightarrow 0^+时的无穷小 α=∫x0cost2dt,β=∫x20tant√dt,γ=∫x</
【数学】常用等价无穷小及其注意事项示例
常用极限 lim x → 0 sin x x = 1 \lim_{x \to 0} {\frac{\sin x}{x}}=1 limx→0xsinx=1 lim x → 0 ( x + 1 ) 1 x = e \lim_{x \to 0} {(x+1)^\frac{1}{x}}=e limx→0(x+1)x1=e lim n → ∞ a n = 1 \lim_{n \t
关于高阶无穷小的解释以及运算
最近在进行一些公式推导时常常被高阶无穷小这个概念折磨的崩溃。高阶无穷小的定义我也看懂了,但是看别人推导公式时突然出现一个高阶无穷小量,仍然看的的我一脸懵逼。通过一天的探究(折磨),终于把高阶无穷小这个概念给弄懂了,原来它是一个集合,并不是一个可以直接纳入代数运算的量,现在将其记下来以帮助以后有类似困惑的人,看完这个博客你至少能解锁如下技能: 1、高阶无穷小到底是个啥玩意 2、再也不用背高阶无穷
图文证明 等价无穷小替换
等价无穷小替换 定义 等价无穷小是无穷小之间的一种关系,指的是:在同一自变量的趋向过程中,若两个无穷小之比的极限为1,则称这两个无穷小是等价的。无穷小等价关系刻画的是两个无穷小趋向于零的速度是相等的。 设当 x → x 0 时, f ( x ) 和 g ( x ) 均为无穷小量。 \text{设当 } x \to x_0 \text{ 时,} f(x) \text{ 和 } g(x)
【高数:3 无穷小与无穷大】
【高数:3 无穷小与无穷大】 1 无穷小与无穷大2 极限运算法则3 极限存在原则4 趋于无穷小的比较 参考书籍:毕文斌, 毛悦悦. Python漫游数学王国[M]. 北京:清华大学出版社,2022. 1 无穷小与无穷大 无穷大在sympy中用两个字母o表示无穷大,正无穷大为sy.oo,负无穷大为-sy.oo import sympy as syx=sy.ooprin
【高数:3 无穷小与无穷大】
【高数:3 无穷小与无穷大】 1 无穷小与无穷大2 极限运算法则3 极限存在原则4 趋于无穷小的比较 参考书籍:毕文斌, 毛悦悦. Python漫游数学王国[M]. 北京:清华大学出版社,2022. 1 无穷小与无穷大 无穷大在sympy中用两个字母o表示无穷大,正无穷大为sy.oo,负无穷大为-sy.oo import sympy as syx=sy.ooprin
c语言 无穷小,C语言中 2%3等于什么 ?
C语言中,2%3等于2。 %是求余运算符,也叫模除运算符,用于求余数。 %要求两个操作数均为整数(或可以隐式转换成整数的类型)。 标准规定: 如果%左边的操作数为负数时,则模除的结果为负数或者0, 如果%左边的操作数为正数时,则模除的结构为正数或者0。 示例代码: #include using namespace std; int main(){ char c = 253; int i =5 ;
高数 | 【极限与等价无穷小】洛必达法则的隐藏细节、广义洛必达法则(分母无穷直接洛必达)使用条件
洛必达使用小结: 发现泰勒展开和等价无穷小代换都搞不定的时候,洛必达判定能否使用: 先看分母,如果趋于0,则看分子是否趋于0;如果分母趋于∞,根据广义洛必达,无需判断分子,即可使用洛必达求解。 对于一些极限类证明题,可以通过构造一个趋于无穷的分母,再使用广义洛必达获得想要的结果。 一、先看洛必达法则的内容 定理的证明:(柯西中值定理) 二、
高数 | 【极限与等价无穷小】来 抓大头与抓小头
一、抓大头 (1)狭义的抓大头 是指求极限 分子分母分别“抓”x的最高次项,忽略低次项。 之所以在分子分母中抓x的最高次项:x趋向于时,最高次项趋向于的速度最快。 (2)广义的抓大头 在求 型未定式极限时,若分子或分母为几项之和,分别取分子分母中趋近最快的无穷大项,忽略趋近速度相对较慢的无穷大项。 当时, 例题: (3)抓大头的推广 若分子分母均是无穷
高数 | 【无穷级数】等价无穷小(Talor展开)判敛法 交错级数不能用通项等价关系审敛
一、引例 我们知道,对于正项级数可以利用所谓的通项等价关系进行审敛,即 废话不多说,看例题 : 二、经错标零 例题你觉得简单?下面这坑你必踩~ 经典的错误,标准的零分~ 关注A选项~ 你的做法: 应用性质:在级数中加上或减去有限项后级数的敛散性不变 设从某一项 N 之后, 运用等价无穷小 如果按照交错级数审敛法(莱布
高数 | 【极限与等价无穷小】两个重要极限 经典错误 什么情况下求极限可以直接带入
可以和这一篇配合食用。 高数 | 等价无穷小量的替换及加减替换条件_西皮呦的博客-CSDN博客_等价无穷小在加减中替换的条件? 可以结合网上等价无穷小是泰勒的粗糙版和 四则运算法中乘法的两个数的极限必须存在 来跟非零因子带入 对比来理解。 一、两个极限存在准则、两个重要极限 1、极限存在准则 夹逼定理(数列和函数极限都适用)、单调有界数列必收敛 对于第二条定理,当运用于函数时需
高数 | 【极限与等价无穷小】常用求极限方法总结
一、利用基本极限求极限 二、利用等价无穷小 三、利用有理运算法则 四、利用洛必达法则 为什么函数二阶可导却不能用两次洛必达法则? ——详见我的相关文章 f(x)二阶可导说明存在f(x)二阶导数存在,但它不一定连续,不连续的话二阶导数的极限就不存在,但是f
极限题型三:确定极限式中的参数 四:无穷小量阶的比较
题型三:确定极限式中的参数 方法:求极限 ①先判断极限的类型 ②将非零极限的因子先提出来 方法一:传统方法,∞-∞型根式差→有理化 方法二:∞-∞型根式差→提无穷因子,先求出a;b回原式看,对原式移项解出b。 方法三:对等式两端同除以x,先求出a;b回原式看,对原式移项解出b。 题型四:无穷小量阶的比较 方法:求型极限的常用三种方法 P40
高数 | 【极限与等价无穷小】等价无穷小量的替换及加减替换条件
可以和这一篇配合食用。 高数 | 复合函数等价无穷小经典错误 & 两个重要极限 & 什么情况下求极限可以直接带入_西皮呦的博客-CSDN博客 一、等价无穷小量的替换的基础知识 1.定义[1] 我们都蛮喜欢用等价无穷小量的替换的,因为在记下了常见的等价无穷小量之后,这种方法我们基本不用复杂的计算。 如果用洛必达法则,我们就要算很长的时间。 2.用等价无穷小量
第二单元 用python学习微积分(十四)无穷小量和不定积分
本文内容来自于学习麻省理工学院公开课:单变量微积分-无穷小量和不定积分-网易公开课 开发环境准备:CSDN 目录 一、无穷小量 二、不定积分 1、 ,这个式子的含义是求谁的导数是sinx 2、 3、 4、 5、 6、 三、例子 1、 2、 3、 4、 5、 6、 一、无穷小量 有函数y = f(x) y的
应用泰勒公式求极限时的无穷小分析
例一 limx→0ln(sin2x+ex)−xln(x2+e2x)−2x \lim_{x_\rightarrow 0}\frac{ln(sin^2x+e^x)-x}{ln(x^2+e^{2x})-2x} 正解: 原式等价于 limx→0ln(sin2x+ex)−lnexln(x2+e2x)−lne2x \lim_{x_\rightarrow 0}\frac{ln