数塔专题

数塔动态规划

Problem Description 在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的：有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？已经告诉你了，这是个DP的题目，你能AC吗? Input 输入数据首先包括一个整数C,表示测试实例的个数，每个测试实例的第一行是一个整数N(1 <= N <= 100

HDU2084_数塔【简单题】【数塔】

数塔 Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 22488 Accepted Submission(s): 13555 Problem Description 在讲述DP算法的

[动态规划] 数塔问题

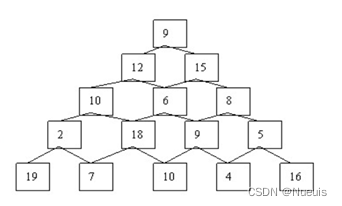
题目给定一个数塔，其存储形式如下图所示：在此数塔中，从顶部出发，每一个节点可以选择向左走或者向右走，一直走到底部，找出一条路径，使路径数值相加结果最大。分析这是一道简单的动态规划题，状态转移是自下向上的，算法思路：假如路径经过第四层2，第五层一定选19假如路径经过第四层18，第五层一定选10假如路径经过第四层9，第五层一定选10假如路径经过第四层5，第五层一定选16把第五层

数塔的变形

聪明的kk 时间限制： 1000 ms | 内存限制： 65535 KB 难度： 3 描述聪明的“KK” 非洲某国展馆的设计灵感源于富有传奇色彩的沙漠中陡然起伏的沙丘，体现出本国不断变换和绚丽多彩的自然风光与城市风貌。展馆由五部分组成，馆内影院播放名为《一眨眼的瞬间》的宽银幕短片，反映了建国以来人民生活水平和城市居住环境的惊人巨变。可移动“沙丘”变戏法的灵感源

数塔动态规划

#include <iostream>using namespace std;#define MAX 20int main(){int i,j,n,a[MAX][MAX];cout<<"请输入塔的层数："<<endl;cin>>n;for(i=0;i<n;++i){cout<<"请输入第"<<i<<"层塔的数据："<<endl;for(j=0;j<=i;++j){cin>

数塔问题（蛮力算法和动态规划）

题目：如下图是一个数塔，从顶部出发在每一个节点可以选择向左或者向右走，一直走到底层，要求找出一条路径，使得路径上的数字之和最大，及路径情况。(使用蛮力算法和动态规划算法分别实现） #include<bits/stdc++.h>#define MAX_SIZE 100 using namespace std;//蛮力算法int maxPathSumForce(int pyramid

数塔问题 (动态规划)

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2084 思路：从上往下推，数越来越多，结果状态太多，不好处理；则由下往上推，越往上数越少，最终归于一个数。(在数塔的最后一层加上n+1个0) 状态方程：dp[i][j] = max(dp[i+1][j], dp[i+1][j+1])+a[i][j]; C++代码实现： #include<stdi

The Triangle--动态规划经典问题--数塔问题

地址：http://acm.nyist.net/JudgeOnline/problem.php?pid=18 The Triangle 时间限制： 1000 ms | 内存限制： 65535 KB 难度： 4

一题多解之数塔问题

递归实现:记忆化+深度遍历 #include <iostream>#include <algorithm>#include <string>using namespace std;int num[1000][1000],n;//递归实现:记忆化+深度遍历int dfs(int x,int y){int sum=0;//记录最大情况if(x>n||y>x) return sum;//

C++数塔问题

#include <iostream>#include <vector>using namespace std;int main() {// 读取输入int n;cin >> n;vector<vector<int>> tower(n, vector<int>(n));for (int i = 0; i < n; i++) {for (int j = 0; j <= i; j++) {cin >

机试:数塔路径

问题描述: 代码示例: //数塔路径#include <bits/stdc++.h>using namespace std;int main(){// 算法思想:// 逆推,将最下方和右下方的数字进行比较,哪个大则加上并更新,直至到根节点即为最大 int n;cin >> n; int nums[n+1][n+1];// 输入数塔 for(int i =1;i <= n;i++){for

HDOJ 2084 数塔【简单DP】

题目详见http://acm.hdu.edu.cn/showproblem.php?pid=2084 题目的意思就是从上到下，找到一个路径加起来和是最大的。这个很简单，就是一个表达式的事，没什么可多想的。遍历是不现实的，也没必要。这个DP 很好想，是我做过最简单的DP了。状态转移方程 array[i][j]+=MAX{array[i-1][j-1]，array[i-1][j]}不多说了，

hdu2084数塔（简单dp）

http://acm.hdu.edu.cn/showproblem.php?pid=2084 数塔 Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others) Total Submission(s): 57124 Accepted Submission(s): 33581 Prob

数塔取数问题

数塔取数问题一个高度为N的由正整数组成的三角形，从上走到下，求经过的数字和的最大值。每次只能走到下一层相邻的数上，例如从第3层的6向下走，只能走到第4层的2或9上。 5 8 4 3 6 9 7 2 9 5 例子中的最优方案是：5 + 8 + 6 + 9 = 28 Input 第1行：N，N为数塔的高度。(2 <= N <= 500) 第2

[ACM] hdu 2084 数塔（简单DP）

Problem Description 在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的：有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？已经告诉你了，这是个DP的题目，你能AC吗? Input 输入数据首先包括一个整数C,表示测试实例的个数，每个测试实例的第一行是一个整数N(1 <=

动态规划2(数塔问题)

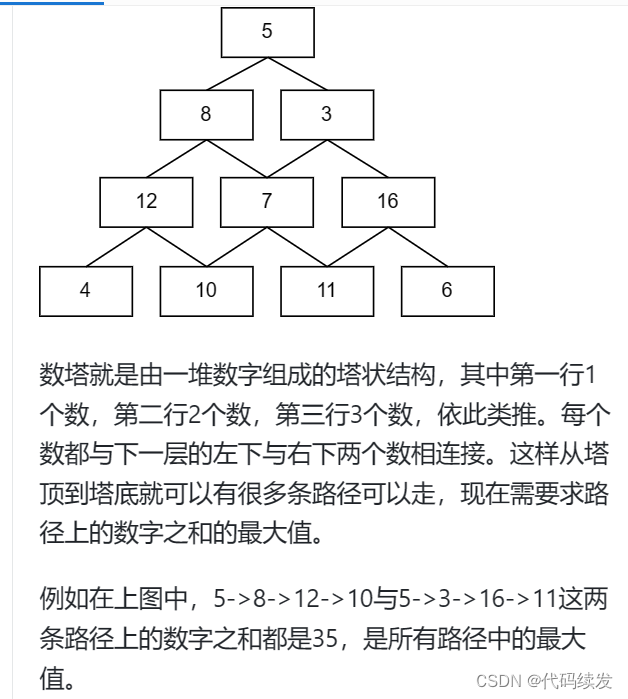
数塔问题是二维情况下动态规划的经典问题，下面以洛谷的一个例题来分析数塔问题以及动态规划：原题链接题目描述观察下面的数字金字塔。写一个程序来查找从最高点到底部任意处结束的路径，使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。在上面的样例中,从7→3→8→7→5 的路径最大输入格式第一个行一个正整数 rr ,表示行的数目。后面每行为这个数字金字塔特定行包

HDU——1176 免费馅饼（动态规划类似数塔问题）

Problem Description 都说天上不会掉馅饼，但有一天gameboy正走在回家的小径上，忽然天上掉下大把大把的馅饼。说来gameboy的人品实在是太好了，这馅饼别处都不掉，就掉落在他身旁的10米范围内。馅饼如果掉在了地上当然就不能吃了，所以gameboy马上卸下身上的背包去接。但由于小径两侧都不能站人，所以他只能在小径上接。由于gameboy平时老呆在房间里玩游戏，虽然在游戏中是个

DP-数塔

题意：从塔顶到塔底，每个点都有一个数字，求一条不能回走的路径，使经过的点的和最大题目链接：数塔解题思路：咳咳，题目都说了是个DP题，那就用DP方法吧！DP有自顶向下和自顶向上两种方法，可以试着比较两种方法。自底向上的状态转移方程dp[i][j]=a[i][j] =max(dp[i+1

动态规划中三角数塔问题(python版本）

###python版本import numpy as npclass triangle_dynatic():def main(self,data):#data塔的原始数据，dp存储动态数据dp = np.zeros(np.array(data).shape)#n为行数，在这里相当于塔数n,m = np.array(data).shape#初始化dp#下面这个循环相当于把data的最后一行付给了

DP Problem F：数塔（HDU 2084）

Problem F Time Limit : 1000/1000ms(Java/Other) Memory Limit : 32768/32768K (Java/Other) Total Submission(s) : 2 AcceptedSubmission(s) : 1 Problem Description 在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的：

数塔问题-算法程序与设计笔记

数塔问题如图所示的一个数塔，从顶部出发，在每一结点可以选择向左走或是向右走，一直走到底层，要求找出一条路径，使路径上的数值和最大。贪心算法：自上而下： 9+15+8+9+10=51 自下而上： 19+2+10+12+9=52 动态规划方法自下而上 1) 原始信息存储原始信息包括层数和数塔中的数据, 层数用一个整型变量n存储, 数塔中的数据用二维数组data, 存储成如下的

【算法设计】动态规划算法设计——天平平衡、数塔问题(C++实现)

创作不易，本篇文章如果帮助到了你，还请点赞关注支持一下♡>𖥦<)!! 主页专栏有更多知识，如有疑问欢迎大家指正讨论，共同进步！更多算法分析与设计知识专栏：算法分析🔥 给大家跳段街舞感谢支持！ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ 目录一、天平平衡问题问题描述算法思想和解题思路C++代码二、数塔问题问题描述算法思想和解题思路C++