数塔问题-算法程序与设计笔记

数塔问题

如图所示的一个数塔，从顶部出发，在每一结点可以选择向左走或是向右走，一直走到底层，要求找出一条路径，使路径上的数值和最大。

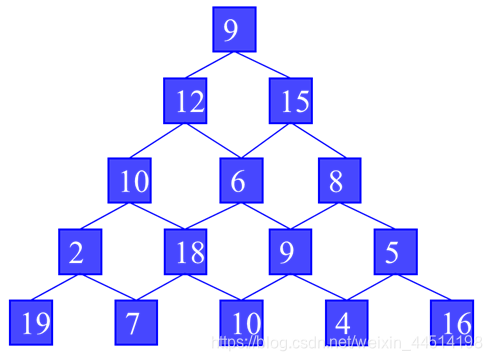
贪心算法：

自上而下：
9+15+8+9+10=51
自下而上：
19+2+10+12+9=52

动态规划方法

自下而上

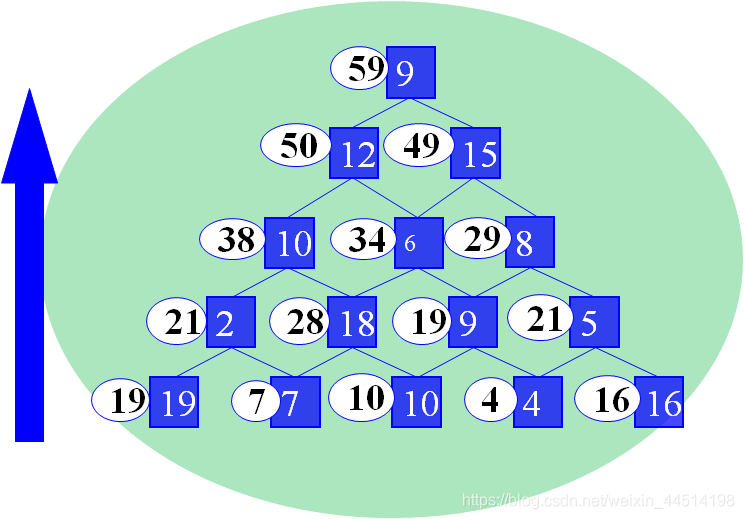
1) 原始信息存储
原始信息包括层数和数塔中的数据,
层数用一个整型变量n存储,
数塔中的数据用二维数组data,
存储成如下的下三角阵:
9
12 15
10 6 8
2 18 9 5
19 7 10 4 16
2) 动态规划过程存储
用二维数组d存储各阶段的
决策结果。二维数组d的存储内容
如下(n:行，j:列)：
step1 d[n][j]=data[n][j] //最低层元素，j=1,2,……,n；
step2 for i=n-1 to 1
for j=1 to i
d[i][j]=max(d[i+1][j]，d[i+1][j+1])+data[i][j]
最后d[1][1]存储的就是问题的结果。

算法代码实现
我们用三维数组a[50][50][3]存储以上确定的三个数组的信息。
a[50][50][1]代替数组data，
a[50][50][2]代替数组d,
a[50][50][3]为解路径标记
(0:向下，1:向右下)。
其中：a[50][50][3]=0表示向“下”走，
a[50][50][3]=1表示向“右下”走

main( )
{ int a[50][50][3],i,j,n; //定义一个三维数组
print( ‘please input the number of rows:’);//输入行数 input(n);　for( i=1 ;i<=n;i++)　　 for j=1 to i do　　 { input(a[i][j][1]);// 输入从塔顶到塔底所对应的数字
　　　 a[i][j][2]=a[i][j][1];//再复制一组数据到另一个数
组，用来存放数据当前的最优　
　　 a[i][j][3]=0;} // 给数组3赋值0，用来记录路径　　
for (i=n-1 ; i>=1;i–)//从塔底的上一层开始寻找路径
for (j=1 ;j>= i ;j++)　　
　if (a[i+1][j][2]>a[i+1][j+1][2])　 {
　 a[i][j][2]=a[i][j][2]+a[i+1][j][2]
　 a[i][j][3]=0;
　 } //表示向下走
　 else {
　 a[i][j][2]=a[i][j][2]+a[i+1][j+1][2] ];
a[i][j][3]=1
｝ //表示向右下方走
print(‘max=’,a[1][1][2]);//输出最大值
j=1;
for( i=1 ;i<= n-1;i++)//输出最优路径 {
print(a[i][j][1],‘->’);
j=j+a[i][j][3];
}
print (a[n][j][1]);
}