【算法设计】动态规划算法设计——天平平衡、数塔问题(C++实现)

本文主要是介绍【算法设计】动态规划算法设计——天平平衡、数塔问题(C++实现)，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

创作不易，本篇文章如果帮助到了你，还请点赞关注支持一下♡>𖥦<)!!
主页专栏有更多知识，如有疑问欢迎大家指正讨论，共同进步！
更多算法分析与设计知识专栏：算法分析🔥
给大家跳段街舞感谢支持！ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ ዽ ጿ ኈ ቼ

在这里插入图片描述

一、天平平衡问题

问题描述

已知一个天平左右两端共有n个挂钩，且有m个不同质量的钩码，求将钩码全部挂到钩子上使天平平衡的方法的总数。试设计求解该问题的动态规划算法。

算法思想和解题思路

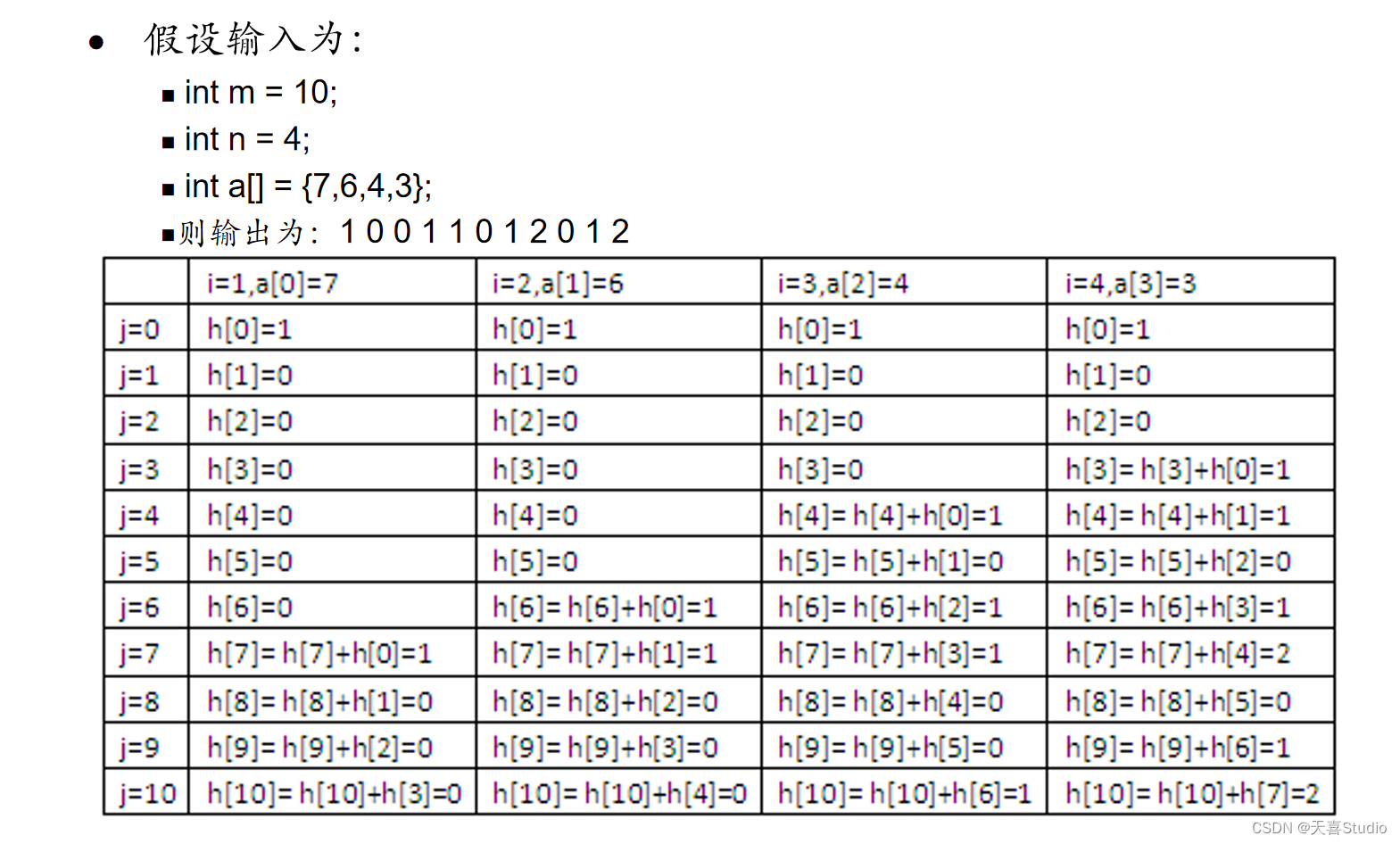
m个钩码要么挂在左边，要么挂在右边，使得左右平衡，也就是说使得左右两边的钩码重量之和相等

左边或者右边的钩码重量之和是全部钩码重量之后的二分之一，天平的两端的重量和为m

从给定的数字数组中选择m个数字，并将它们分配到天平的两边，使得左右两边的数字之和相等

判断当前钩码的重量是否大于等于j，如果是的话，就将dp[j]加上dp[j - 当前钩码的重量]

	dp[j] = dp[j] + dp[j - arr[i - 1]];

定义状态：dp[i]表示总重量为i时可以形成的平衡重量组合的数量。然后通过遍历每个钩码，尝试将这个钩码放到左边或者不使用这个钩码，然后更新dp数组
状态转移方程：当前钩码的重量是否大于等于j，如果是则 dp[j] = dp[j] + dp[j - arr[i - 1]]; // 将dp[j]加上dp[j - 当前钩码的重量]
边界条件：当没有钩码时，只有一种方案，即dp[0] = 1

在这里插入图片描述

C++代码

#include <iostream>
using namespace std;void sumMethod(int m,int n,int arr[])
{int dp[100] = { 0 };dp[0] = 1;for (int i = 1; i <= n; i++)		// 对钩码数量n进行循环  {for (int j = m; j >=1; j--)	// 对全部钩码的重量之和的二分之一m进行循环  {if (j >= arr[i - 1])		// 如果j大于等于当前钩码的重量  {dp[j] = dp[j] + dp[j - arr[i - 1]];	// 则将dp[j]加上dp[j - 当前钩码的重量]}}}for (int j = 0; j <= m; j++)	// 对全部钩码的重量之和的二分之一m进行循环  {  cout << dp[j] << " ";}cout << endl;
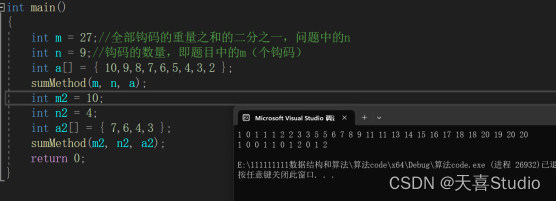
}int main()
{int m = 27;//全部钩码的重量之和的二分之一，问题中的nint n = 9;//钩码的数量，即题目中的m（个钩码）int a[] = { 10,9,8,7,6,5,4,3,2 };sumMethod(m, n, a);int m2 = 10;int n2 = 4;int a2[] = { 7,6,4,3 };sumMethod(m2, n2, a2);return 0;
}

在这里插入图片描述

二、数塔问题

问题描述

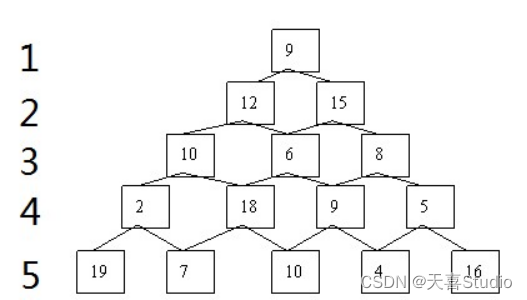
对于诸如下图的数塔，若从顶层走到底层，每一步只能走到相邻的结点，求经过的结点的数字之和最大的路径

试设计求解该问题的动态规划算法

在这里插入图片描述

算法思想和解题思路

从数塔的顶部开始，对于每个位置，选择向左走还是向右走，使得走过的路径上的数字之和最大

在数塔问题中，我们可以用一个二维数组dp来保存每个位置的最大值

定义状态：data[i][j]表示数塔中位置(i, j)上的数字，对于每个位置(i, j)，我们可以通过比较从左侧位置(i+1, j)和右侧位置(i+1, j+1)的最大值，来决定是从左走还是从右走
状态转移方程：dp[i][j] = max(dp[i+1][j], dp[i+1][j+1]) + data[i][j]
边界条件：dp[0][0]为数塔底部位置的最大值。

C++代码

#include <iostream>
#include <string.h>
#include <algorithm>
using namespace std;
void maxSum(int n)
{int arr[100][100];int dp[100][100];cout << "输入数塔:" << endl;for (int i = 0; i < n; i++){for (int j = 0; j <= i; j++){cin >> arr[i][j];dp[i][j] = arr[i][j];}}for (int i = n - 2; i >= 0; i--){for (int j = 0; j <= i; j++){dp[i][j] += max(dp[i + 1][j], dp[i + 1][j + 1]);}}cout << "数字之和最大为：" << dp[0][0] << endl;
}
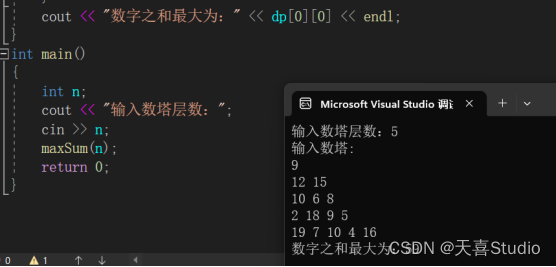
int main()
{int n;cout << "输入数塔层数：";cin >> n;maxSum(n);return 0;
}