抽样专题
通信原理抽样定理和PAM调制解调硬件实验
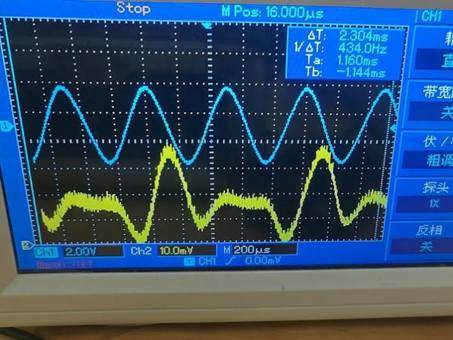
一、实验目的 1. 加深理解抽样定理; 2. 加深理解脉冲幅度调制的原理。 二、实验内容 1. 观测PAM平顶抽样波形; 2. 观测PAM自然抽样波形及解码后波形。 三、实验器材 1. 双踪示波器; 2. 通信原理实验箱信号源模块、①号模块。 四、实验步骤 1. 观测PAM平顶抽样波形 (1)用示波器观测信号源“2K同步正弦波”输出,调节W1改变输出信号幅度,使输出信号峰峰值
压缩感知与Nquist抽样定理——模拟信息转换(AIC)学习总结
原文链接:http://blog.csdn.net/jbb0523/article/details/41595535 一、引言 压缩感知(CompressiveSensing, or Compressed Sensing)或译为压缩传感,或者称为压缩采样(Compressive sampling),以下统称压缩感知,简称CS。 在压缩感知的有关文献中几乎都在说“压缩感知突破了传统的Nq
大数据算法-空间时间亚线性算法举例(水库抽样,平面图直径)
大数据算法-空间时间亚线性算法举例 水库抽样 问题描述 Input:一组数据 Output:这组数据的K个均匀抽样要求: 扫描一次空间复杂度o(k)扫描到前n个数字时,保存当前数据的均匀抽样实现 收到第i个元素t时,以k/i的概率随机替换抽样数组ans[]中的元素证明 均匀: ki×(1−1i+1)×(1−1i+2)×⋯×(1−1n)=kn \frac{k}{i}\tim
Llama模型家族之拒绝抽样(Rejection Sampling)(九) 强化学习之Rejection Sampling
LlaMA 3 系列博客 基于 LlaMA 3 + LangGraph 在windows本地部署大模型 (一) 基于 LlaMA 3 + LangGraph 在windows本地部署大模型 (二) 基于 LlaMA 3 + LangGraph 在windows本地部署大模型 (三) 基于 LlaMA 3 + LangGraph 在windows本地部署大模型 (四) 基于 LlaMA 3
从0开始学统计-战斗机保护和代表性抽样
1.什么是抽样研究?为什么要做抽样研究? 抽样研究是一种研究方法,它涉及从整体人群或群体中选取一部分样本来代表整体,以进行研究和推断。在抽样研究中,研究者从总体中选择一个相对较小的样本,通过对这个样本进行观察、实验或调查来推断总体的特征、趋势或关系。 抽样研究的目的在于: (1)节省时间和成本: 通过研究样本而不是整个总体,可以节省大量的时间和资源。这样的方法通常更经济高效。 (2)可行性
Hive中分桶及抽样查询
1.分桶表 分桶表数据存储 分区针对的是数据的存储路径;分桶针对的是数据文件 分区提供一个隔离数据和优化查询的便利方式。不过,并非所有的数据集都可形成合理的分区,特别是之前所提到过的要确定合适的划分大小这个疑虑。 分桶是将数据集分解成更容易管理的若干部分的另一个技术 数据准备 student.txt 1001 ss1
【统计推断】-01 抽样原理之(四):中心极限定律
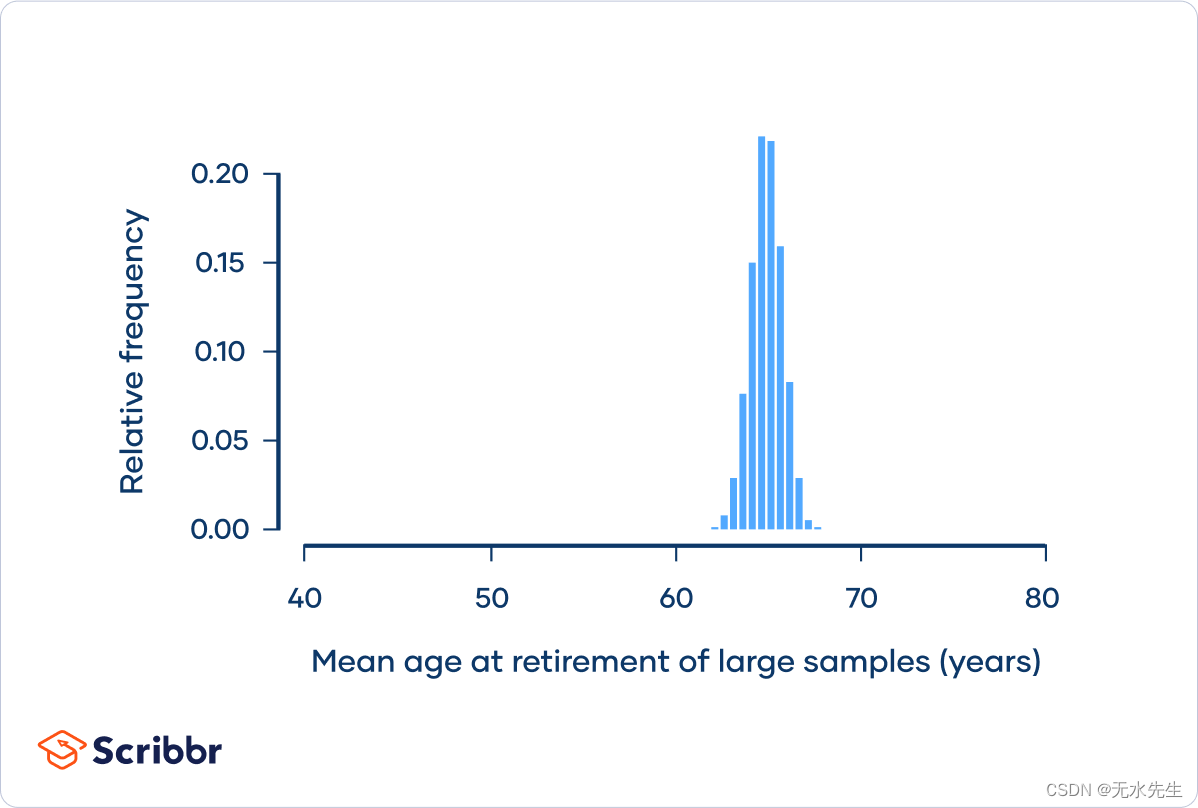
文章目录 一、说明二、样本均值的抽样分布三、两个重要公理四、中心极限定理4.1 定义4.2 中心极限定理的特点4.3 中心极限定理的条件 五、一个举例5.1 一个连续分布示例5.2 样本容量变化的对比 六、结论 关键词: Central Limit Theorem Law of Large Numbers 一、说明 大数定律和中心极限定律无疑是抽样理论最
【统计推断】-01 抽样原理之(三)
文章目录 一、说明二、抽样分布三 均值抽样分布3.1 有限母体无放回抽样3.2 有限母体有放回抽样3.3 无限母体 四、比例抽样分布五、和差抽样分布 一、说明 上文中叙述母体和抽样的设计;以及抽样分布的概念,本篇将这种关系定量化,专门针对抽样的指标参数和母体参数的对应关系,这是我们以后做检验的基础。 二、抽样分布 考虑从给定的母体中抽取容量为N的所有可能样本(抽样
【统计推断】-01 抽样原理之(二)
上篇文章:【统计推断】-01 抽样原理之(一) 关键词:Sampling distribution 目录 一、说明二、抽样分布的定义、用法和示例2.1 什么是抽样分布?2.2 抽样分布如何工作 三、确定抽样分布四、抽样分布的类型五、绘制抽样分布图六、为什么使用抽样来收集人口数据?七、为什么使用抽样分布?八、什么是均值?九、底线 一、说明 本篇是对上一篇文章(【统计推断】-01
竞争性自适应加权抽样结合偏最小二乘回归(CARS-PLS)在多变量分析中的应用(附MATLAB软件包)
竞争性自适应加权抽样结合偏最小二乘回归(CARS-PLS)在多变量分析中的应用 引言 在现代科学研究中,高维数据分析是一个日益重要的课题。由光谱学、色谱学和其他高通量测量技术产生的数据集通常包含大量的冗余和噪声,这给模型建立和预测带来了挑战。竞争性自适应加权抽样结合偏最小二乘回归(CARS-PLS)方法作为一种新兴的多变量分析工具,已经在多个科学领域展示了其强大的特性。本文将深入探讨CARS-
[Hive]Hive实现抽样查询
对于非常大的数据集,有时用户需要使用的知识一个具有代表性的查询结果,而不是全部结果。Hive可以通过对表进行分桶抽样来满足这个需求。 1、分桶抽样查询 select * from numbers TABLESAMPLE(BUCKET 3 OUT OF 10 ON number) s; 其中tablesample是抽样语句,语法:TABLESAMPLE(BUCKET x OUT OF y)
群狼调研(长沙市场调研)行政大厅满意度抽样方法
行政大厅满意度调查的抽样方法是确保调查结果能够准确代表整个受众群体的关键一步。以下是一些常用的抽样方法,可以根据实际情况选择其中之一或多种相结合: 1.随机抽样: 在整个受众群体中随机选择一定数量的个体作为样本,确保每个个体有相等的机会被选中。随机抽样可以减少偏见,提高样本的代表性。 2.分层抽样: 将受众群体按照某些特征(如性别、年龄、职业等)分成不同的层次,然后从每个层次中抽取样本。这样可以确
面试题80:海量数据等概论抽样(蓄水池问题)
题目: 从N个元素中随机抽取K个元素,N的个数不确定,要求保证每个数字被抽中的概率相等。 解读: 这种应用的场景一般是数据流的情况下,由于数据只能被读取一次,而且数据量很大,并不能全部保存,因此数据量N是无法在抽样开始时确定的;但又要保证概率相等。 解决: 解决方案就是蓄水池抽样。主要思想就是保持一个集合(这个集合最终的数字就是被抽中的数字)。依次遍历所有数据的时候以一定的概率替换掉这个
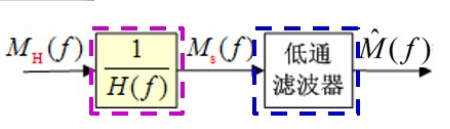
带限信号的抽样与恢复
带限信号的抽样与恢复 x ( t ) x(t) x(t)为带限信号,即对于 ∣ f ∣ ≥ W , X ( f ) = 0 \vert f \vert \geq W, X(f) = 0 ∣f∣≥W,X(f)=0根据奈奎斯特抽样定律,只要抽样频率 1 T s ≥ 2 W \frac{1}{T_s} \geq 2W Ts1≥2W即可无损恢复出信号 x ( t ) x(t) x(t)。且
【基于概率比例抽样的PPS抽样】
文章目录 前言什么是PPS抽样?PPS抽样的使用步骤1. 确定总体2. 计算个体的大小(比例)3. 计算个体被选入样本的概率4. 抽取样本 示例 前言 概率比例抽样(Probability Proportional to Size Sampling,简称PPS抽样)是一种经典的抽样方法,它可以在考虑总体分布的情况下,以更高效的方式获取样本。 什么是PPS抽样? PPS抽样是
抽样算法——【数据科学与工程算法基础】
一、前言 这是课程的第二章节——抽样算法,主要分为三类。 详情可参考: 数据科学的算法基础——学习记录跳转中心 二、正篇 1.系统抽样 课本只介绍了最简单的——等距抽样。 直线等距抽样(N=n*k):即总体个数可以被抽样个数整除时,每隔k个取一个样本,第一个可能给出,可能随机。
【MATLAB第100期】基于MATLAB的多种改进拉丁超立方LHS数据抽样方法
【MATLAB第100期】基于MATLAB的多种改进拉丁超立方LHS数据抽样方法 一、LHS种类 1、LHS 使用随机搜索生成拉丁超立方体样本。LHS函数特别适用于非常大的设计,当本机MATLAB函数内存不足时。这可能取决于MATLAB版本和所用机器的配置。当尝试运行“lhsdesign”但未成功时,此功能最有用。设计的每一行代表一个点(或样本)。设计变量被规范化,使得超立方体点的值在0
随机森林 bagging袋装法(基于bootstrap重抽样自举法)的原理与python实现——机器学习笔记之集成学习 Part 1
* * * The Machine Learning Noting Series * * * 导航 1 Bootstrap重抽样自举法 2 袋装法(Bagging) 3 随机森林 4 python实现——一个实例 ⚫袋装法和随机森林过程基本一样,都是根据bootstrap的一系列样本分别建立决策树,然后用这些决策树投票出结果。最大区别,也就是随机森林更好的原因在于:随机森林在建立
随机算法之蓄水池抽样问题
蓄水池抽样问题是从动态变化的N个元素中随机抽选出M个元素(N>=M) 算法描述如下: Init : a reservoir with the size: kfor i= k+1 to NM=random(1, i);if( M < k)SWAP the Mth value and ith valueend for 由于N的个数是不确定的,这就意味着不论N的个数是多少,里面元素都要
压缩感知与Nquist抽样定理——模拟信息转换(AIC)学习总结
原文链接:http://blog.csdn.net/jbb0523/article/details/41595535 一、引言 压缩感知(CompressiveSensing, or Compressed Sensing)或译为压缩传感,或者称为压缩采样(Compressive sampling),以下统称压缩感知,简称CS。 在压缩感知的有关文献中几乎都在说“压缩感知突破了传统的Nq
数据分析(4)——闲话抽样
中国的人口普查大名鼎鼎,这里的普查是指对总体的研究和调查,普查内容包括人的基本情况、迁移流动状况、人口素质情况,就业、社会保障状况、婚姻生育状况等多项内容。但是中国的人口过于庞大,不可能对每个人都进行调查,这样一来,抽样就显得十分重要。在抽样之前,先来看看数据是如何获取的。 获取数据 大多数时候,我们获取数据的方式仅仅是坐在计算机前查看某个数据库或解析某个流式文件,在进行这种行为时,
《统计学简易速速上手小册》第3章:概率分布与抽样技术(2024 最新版)
文章目录 3.1 重要的概率分布3.1.1 基础知识3.1.2 主要案例:顾客到访分析3.1.3 拓展案例 1:产品缺陷率分析3.1.4 拓展案例 2:日销售额预测 3.2 抽样方法与推断3.2.1 基础知识3.2.2 主要案例:顾客满意度调查3.2.2 拓展案例 1:新产品测试3.2.4 拓展案例 2:员工满意度调查 3.3 应用抽样技术3.3.1 基础知识3.3.2 主要案例:用户体