【统计推断】-01 抽样原理之（四）：中心极限定律

本文主要是介绍【统计推断】-01 抽样原理之（四）：中心极限定律，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

关键词：
   Central Limit Theorem
   Law of Large Numbers

一、说明

   大数定律和中心极限定律无疑是抽样理论最重要的理论支持。注意这两个定律是以公理形式出现，因此不要试图证明。有种种案例可以强化对这两个公理的理解。本篇将叙述两个公理意义，合理性，约束条件。从直观上加强对这个理论的理解。

二、样本均值的抽样分布

   为了了解如何使用抽样误差，我们将了解一种新的理论分布，称为抽样分布。就像我们可以收集许多单独的分数并将它们放在一起形成具有中心和分布的分布一样，如果我们要采取许多大小相同的样本，并计算每个样本的平均值，我们可以将这些手段放在一起形成一个分布。
   直观上，这种新分布被称为样本均值分布。这是我们所说的抽样分布的一个例子，我们可以由一组任何统计量组成，例如均值、检验统计量或相关系数（后两者将在第 2 单元和第 3 单元中详细介绍）。出于我们的目的，了解样本均值的分布就足以了解所有其他抽样分布如何工作以支持和告知我们的推理分析，因此从现在开始这两个术语将互换使用。让我们更深入地了解它的一些特征。

   样本均值的抽样分布可以通过其形状、中心和分布来描述，就像我们使用过的任何其他分布一样。我们的采样分布的形状是正态的：钟形曲线，有一个峰和两个在任一方向对称延伸的尾部，就像我们在前面的章节中看到的那样。样本均值的抽样分布中心（即均值本身或平均值）是真实总体均值，μ。有时这会写成${\mu }_{\bar{x}}$ 将其表示为样本均值的平均值。抽样分布的分布称为标准误差，抽样误差的量化，表示为${\mu }_{\bar{x}}$。标准误差的公式为：
$${\sigma }_{\bar{x}}=\frac{\sigma }{\sqrt{n}}$$
   请注意，样本大小在此等式中。如上所述，抽样分布是指特定大小的样本。也就是说，所有样本均值必须根据相同大小的样本计算得出n
， 这样的n= 10,n= 30，或n= 100。此样本量是指每个样本中有多少人或观察值，而不是用于形成抽样分布的样本数。这是因为抽样分布是一种理论分布，而不是我们实际计算或观察的分布。fig 6.2. 1以图形形式显示此处所述的原则。

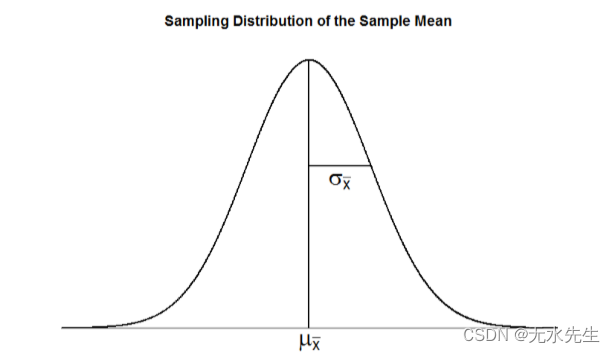
fig 6.2. 1 ：样本均值的抽样分布

三、两个重要公理

   我们刚刚了解到抽样分布是理论上的：我们从未真正看到过它。如果这是真的，那么我们怎么知道它有效呢？我们如何使用我们看不到的东西？答案在于两个非常重要的数学事实：中心极限定理和大数定律。我们不会深入研究这些陈述是如何得出的，但了解它们是什么以及它们的含义对于理解推论统计为何有效以及我们如何根据从单个样本获得的信息得出关于总体的结论非常重要。

四、中心极限定理

4.1 定义

   中心极限定理指出，如果从总体中抽取足够大的样本，则即使总体不是正态分布，样本均值也将呈正态分布。
   总体遵循泊松分布（左图）。如果我们从总体中抽取 10,000 个样本，每个样本大小为 50，则样本均值遵循正态分布，正如中心极限定理（右图）所预测的那样。

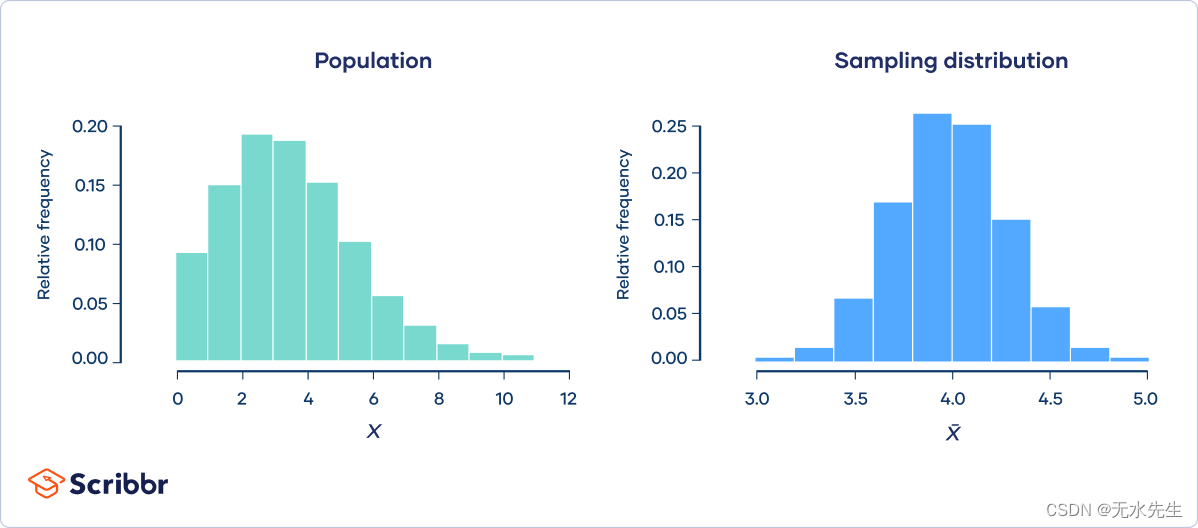
   中心极限定理指出：

   定理3.1 对于单一尺寸n的抽样，从具有给定均值的总体中抽取μ和方差${\sigma }^2$，样本均值的抽样分布将有一个均值${\mu }_{\bar{x}}=\mu$和方差${\sigma }_{\bar{x}}^2=\frac{{\sigma }^2}{n}$。随n的增加，该分布将接近正态分布，如下所示。

   由此，我们能够找到抽样分布的标准差，即标准误差。正如您所看到的，就像任何其他标准差一样，标准误差只是分布方差的平方根。

   中心极限定理的最后一句指出，随着用于创建抽样分布的样本量的增加，抽样分布将呈正态分布。这意味着更大的样本将创建更正态的分布，因此我们能够更好地使用我们为正态分布和概率开发的技术。那么多大才算足够大呢？一般来说，如果两个特征之一为真，则抽样分布将是正态分布：

• 从中抽取样本的母体呈正态分布（此时无论样本容量是否足够大）
• 样本容量等于或大于 30。
     第二个标准非常重要，因为它使我们能够使用为正态分布开发的方法，即使真实的总体分布是倾斜的。

4.2 中心极限定理的特点

   中心极限定理依赖于抽样分布的概念，它是从总体中抽取的大量样本的统计量的概率分布。
   想象一个实验可以帮助您理解抽样分布：

• 假设您从总体中抽取一个随机样本并计算该样本的统计数据，例如平均值。
• 现在，您抽取另一个相同大小的随机样本，并再次计算平均值。
• 您多次重复此过程，最终会得到大量均值，每个样本一个。
  样本均值的分布是抽样分布的一个示例。

   中心极限定理表明，只要样本量足够大，均值的抽样分布将始终呈正态分布。无论总体是否服从正态分布、泊松分布、二项分布或任何其他分布，均值的抽样分布都将是正态分布。

   正态分布是一种对称的钟形分布，离分布中心越远，观测值就越少。

4.3 中心极限定理的条件

中心极限定理指出，在以下条件下，均值的抽样分布将始终遵循正态分布：

• 样本量足够大。如果样本量n ≥ 30，则通常满足此条件。
• 样本是独立同分布 (iid) 随机变量。如果抽样是随机的，则通常会满足此条件。
• 总体分布具有有限方差。中心极限定理不适用于具有无限方差的分布，例如柯西分布。大多数分布具有有限方差。

五、一个举例

5.1 一个连续分布示例

假设您对美国人们的退休年龄感兴趣。人口都是退休的美国人，人口分布可能如下所示：

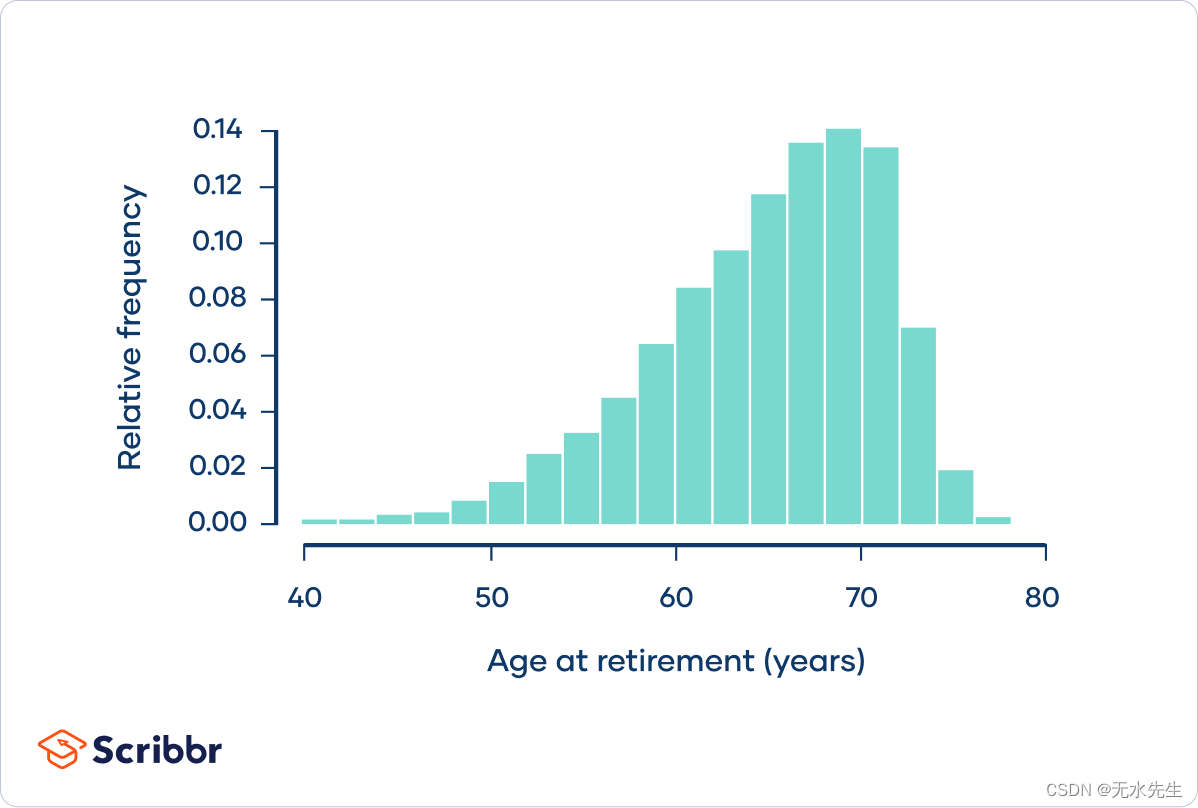
   退休年龄遵循左偏分布。大多数人在平均退休年龄 65 岁的大约五年内退休。然而，存在一个“长尾”，即退休年龄更早的人，例如 50 岁甚至 40 岁。人口的标准差为 6 年。

   想象一下，您从总体中抽取了一小部分样本。您随机选择五名退休人员并询问他们退休的年龄。

5.2 样本容量变化的对比

例子：中心极限定理；n = 5的样本
68 73 70 62 63

样本平均值是总体平均值的估计值。这可能不是一个非常精确的估计，因为样本量只有 5 个。

例子：中心极限定理；小样本的平均值
mean = (68 + 73 + 70 + 62 + 63) / 5 = 67.2 岁

假设您重复此过程 10 次，抽取 5 名退休人员的样本，并计算每个样本的平均值。这是均值的抽样分布。

例子：中心极限定理； 10 个小样本的平均值>
60.8 57.8 62.2 68.6 67.4 67.8 68.3 65.6 66.5 62.1

如果多次重复该过程，样本均值的直方图将如下所示：

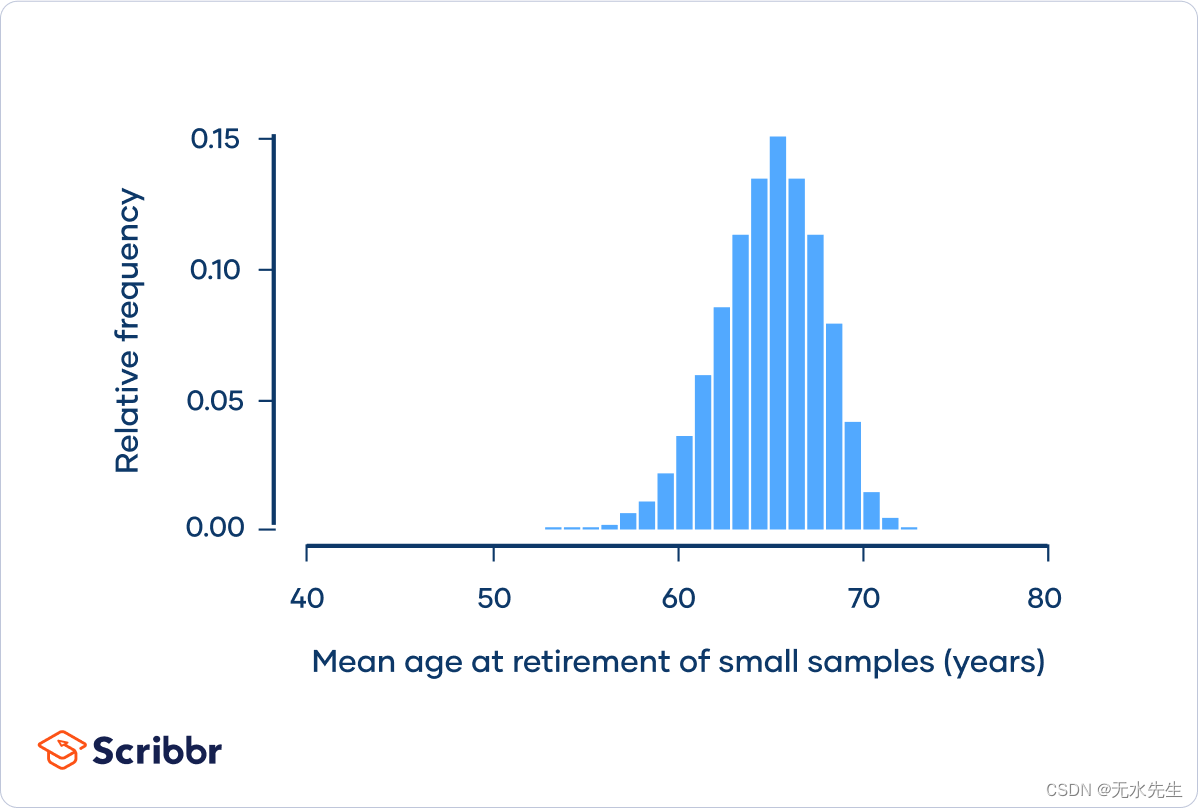
虽然这种抽样分布比总体分布更正态分布，但它仍然有一点左偏。

另请注意，抽样分布的分布小于总体的分布。

中心极限定理表明，当样本量足够大时，均值的抽样分布将始终遵循正态分布。这种平均值的抽样分布不是正态分布，因为它的样本量不够大。

现在，想象一下您抽取了大量人口样本。您随机选择 50 名退休人员并询问他们退休年龄。

例子：中心极限定理；n = 50的样本
73 49 62 68 72 71 65 60 69 61
62 75 66 63 66 68 76 68 54 74
68 60 72 63 57 64 65 59 72 52
52 72 69 62 68 64 60 65 53 69
59 68 67 71 69 70 52 62 64 68
样本平均值是总体平均值的估计值。这是一个精确的估计，因为样本量很大。

例子：中心极限定理；大样本的平均值
mean = 64.8 岁

同样，您可以多次重复此过程，抽取 50 名退休人员的样本，并计算每个样本的平均值：

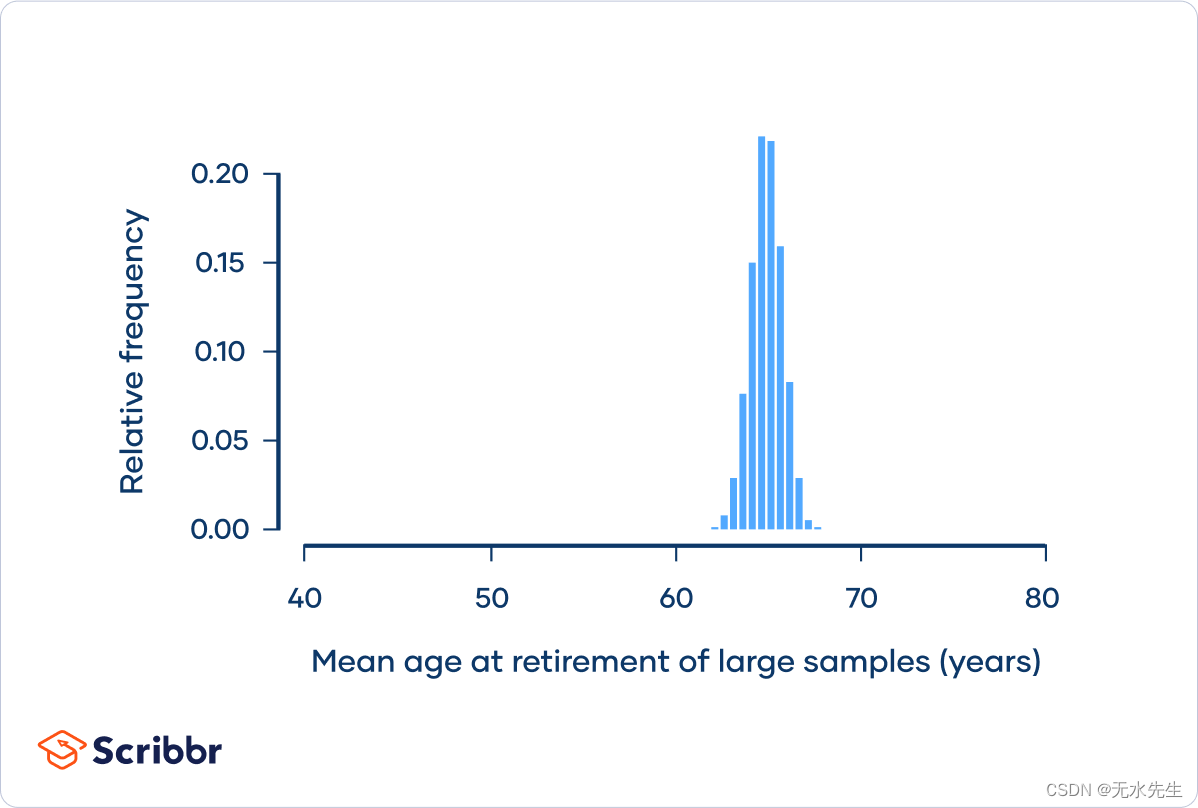
在直方图中，您可以看到此采样分布呈正态分布，正如中心极限定理所预测的那样。

该抽样分布的标准差为0.85年，小于小样本抽样分布的散布，也远小于总体的散布。如果进一步增加样本量，差异会进一步减小。

我们可以用中心极限定理公式来描述抽样分布：

$\bar{X}\sim N(\mu ,\frac{\sigma }{\sqrt{n}})$
$\mu =65$
$\sigma =6$
$N=50$
$\bar{X}\sim N(65,\frac{6}{\sqrt{50}})$
$\bar{X}\sim N(65,0.85)$

六、结论

本篇在中心极限定理上已经消耗了足够的篇幅，我们将在续篇中阐述大数定律和以及切比雪夫不等式。

这篇关于【统计推断】-01 抽样原理之（四）：中心极限定律的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---