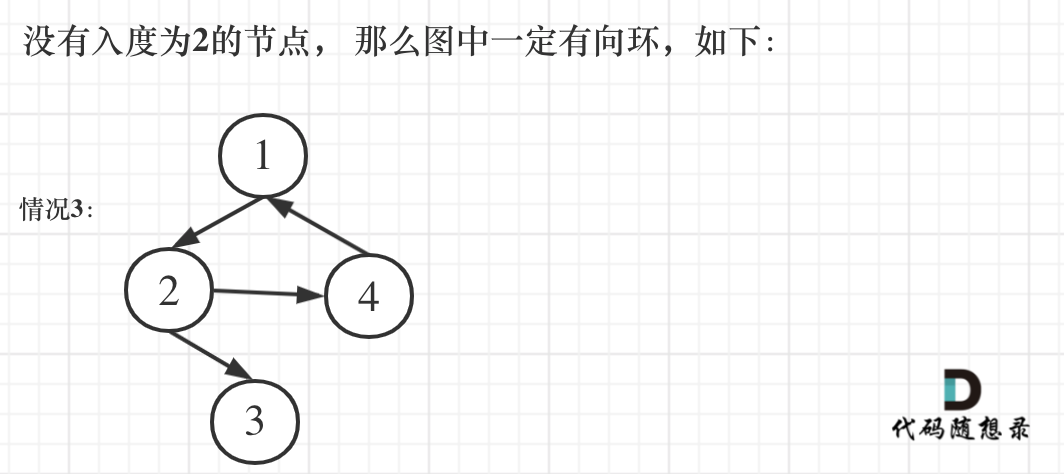
图中专题
【408DS算法题】039进阶-判断图中路径是否存在
Index 题目分析实现总结 题目 对于给定的图G,设计函数实现判断G中是否含有从start结点到stop结点的路径。 分析实现 对于图的路径的存在性判断,有两种做法:(本文的实现均基于邻接矩阵存储方式的图) 1.图的BFS BFS的思路相对比较直观——从起始结点出发进行层次遍历,遍历过程中遇到结点i就表示存在路径start->i,故只需判断每个结点i是否就是stop
最短路径算法:迪杰克斯拉(Dijkstra)算法(基于贪心思想)【从一个顶点到其余各顶点的最短路径算法,解决的是有权图中最短路径问题】【能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低】
Dijkstra算法是典型最短路算法,用于计算一个节点到其他所有节点的最短路径。主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。Dijkstra算法能得出最短路径的最优解,但由于它遍历计算的节点很多,所以效率低。 Viterbi和Dijkstra算法看起来比较像,两者的区别: Dijkstra算法适应范围更广。Viterbi算法用在特殊的有向无环图中,而Dijkstra算法可以用在
DFS、BFS、Union-Find:找出图中省份数量的最佳方法
题目理解 问题描述: 有 n 个城市,其中一些城市之间直接相连,另一些则不相连。如果城市 a 和城市 b 直接相连,且城市 b 和城市 c 直接相连,那么城市 a 和城市 c 间接相连。省份被定义为一组直接或间接相连的城市,组内不包含与之不相连的其他城市。给定一个 n x n 的矩阵 isConnected,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直
【uml】之类图中的关系
uml早就画完了图,但是自己迟迟没有总结,因为总觉的自己把握的不到位,虽然现在也还是不到位,废话少说,上篇博客总结了用例图中的几种关系,这篇就讨论一下类图中的几种关系。 在uml的所有图中,就我目前的水平,我觉得用例图和类图是最重要的,用例图上次已经介绍过了,这篇主要介绍类图,想要画好类图,就要先学会抽象类!之前我一直纠结于类图该如何抽象,问了几个人
关于图中节点间的概率求解问题-1
前提:节点是含有若干特征(小节点)的大节点,大节点间连接实际为特征间的连接 在一个网络图中,若干节点之间的概率问题有以下几种: 设现有A,B,C等若干大节点,其内特征为ai,bj,ck; P(A); //数出A节点发散的所有边的数量除以图中出现的总边数 P(AB); //即P(A)*P(B),原理同上 P(A,B); //此为联合概率,如果AB之间不相联系,则直接为零 P(
关于图中节点间的概率求解问题-2,未完探究中
最近在贝叶斯网络上遇到了难题,简单而言就是怎么求两个节点间的概率。 此问题的前提是,节点为大节点,内有若干特征,节点间的连接(或称为连线)实际为特征之间的连线。且两节点不是孤立的,而是在一个网络(或称一个图)中。 现在的方法是: 利用已知的特征之间的边,来分别计算边的条数,直接用条数来计算概率。 example: 求条件概率P(A|B),A内有 a0,a1,a2;B内有b0,b1;
关于图中节点间的概率求解问题
(本文年代久远,请谨慎阅读)前提:节点是含有若干特征(小节点)的大节点,大节点间连接实际为特征间的连接 在一个网络图中,若干节点之间的概率问题有以下几种: 设现有A,B,C等若干大节点,其内特征为ai,bj,ck; P(A); //数出A节点发散的所有边的数量除以图中出现的总边数P(AB); //即P(A)*P(B),原理同上P(A,B); //此为联合概率,如果AB之间不相联系,则直接为零P
如何从用户旅程图中挖掘差异化需求?
同一品类产品往往数量庞大,作为新入局的产品,需要打造差异化,才能脱颖而出。具体该如何做?本文作者从用户旅程图出发,结合相关案例,对不同阶段如何打造差异点展开了分析总结,与大家分享。 一个产品往往不止满足一个用户需求,或者说一个产品是多种用户需求的集合。简单的产品如笔,基本就是拿来写字的,满足写字一种需求。复杂的产品如手机,满足了非常多的用户需求,如通话、视频、音乐、娱乐、游戏、社交等等
2024.4.27力扣每日一题——查询网格图中每一列的宽度
2024.4.27 题目来源我的题解方法一 遍历方法二 优化 题目来源 力扣每日一题;题序:2639 我的题解 方法一 遍历 遍历每一列的所有数字,并计算长度,取其中最大的作为这一列的结果 时间复杂度:O(nmC)。C表示数字的最大 字符串长度 空间复杂度:O(1) public int[] findColumnWidth(int[][] grid)
计算图中反向传播求导权重矩阵需要转置的说明
在计算图中,基于链式法则的计算图反向求导是模型训练的关键算法,下面用图例说明为什么反向传播的时候,权重矩阵需要转置 按着图中箭头方向“从左向右进行计算”称为正向传播,即从计算图的出发点到结束点的传播, “从右往左计算”称为反向传播. 另一个例子: 当反向传播进来的是误差对上一层的导数时,反向传播矩阵使用正向传播矩阵的转置. 结束!
loadrunner负载测试中windows资源监控图中哪三条线代表 CPU 、内存 、磁盘IO 求把度量名列出来
cpu占用率:%processor time(processor_total)可用内存:available MBytes(memory)磁盘io:disk transfers/sec(physicalDisk_total)
python实现Dijkstra算法求解图中最短路径距离
继续上一篇博文的内容,这里要做的是Dijkstra算法,与Floyd算法类似,二者的用途均为求解最短路径距离,在图中有着广泛的应用,二者的原理都是老生常谈了,毕竟本科学习数据结构的同学是不可能不学习这两个算法的,所以在这里我也不再累赘,只简单概述一下这个算法的核心思想: Dijkstra算法的输入有两个参数,一个是原始的数据矩阵,一个是起始的顶点下标,算法的思想也很简单容易理解,
【单源最短路 图论】882. 细分图中的可到达节点
作者推荐 视频算法专题 本文涉及知识点 单源最短路 图论 LeetCode 882. 细分图中的可到达节点 给你一个无向图(原始图),图中有 n 个节点,编号从 0 到 n - 1 。你决定将图中的每条边 细分 为一条节点链,每条边之间的新节点数各不相同。 图用由边组成的二维数组 edges 表示,其中 edges[i] = [ui, vi, cnti] 表示原始图中节点 ui 和 vi
数据结构图中极大连通子图和极小连通子图的区别
极大连通子图要求该连通子图要包含其所有的边 极小连通子图是在保持图连通的情况下,使得边数最少(即删除多余的边) 极小连通子图可以看作在极大连通子图的基础上删除多余的边
论文浅尝 | ERNIE-ViL:从场景图中获取结构化知识来学习视觉语言联合表示
笔记整理:朱珈徵,天津大学硕士 链接:https://www.aaai.org/AAAI21Papers/AAAI-6208.YuFei.pdf 动机 现有的视觉语言预训练方法试图通过在大的图像文本数据集上的视觉基础任务来学习联合表示,包括基于随机掩码子词的掩码语言建模、掩码区域预测和图像/文本级别的图像-文本匹配。然而,基于随机掩蔽和预测子词,目前的模型没有区分普通词和描述详细语义的词。
并查集|1971. 寻找图中是否存在路径、684.冗余连接、685.冗余连接II
目录 并查集基础 1971. 寻找图中是否存在路径 684.冗余连接 685.冗余连接II 并查集基础 并查集主要有三个功能。 寻找根节点,函数:find(int u),也就是判断这个节点的祖先节点是哪个将两个节点接入到同一个集合,函数:join(int u, int v),将两个节点连在同一个根节点上判断两个节点是否在同一个集合,函数:isSame(int u, int v
操盘机器人闪亮登场,不出意外大盘还将回调2到3天,图中虚线用于预测大盘走势从未失误过哦
不出意外大盘还将回调2到3天,图中虚线用于预测大盘走势从未失误过哦 1、具备各种分析指标及模型,能自动分析选股 2、能自动做T,自动下单买卖 3、具备实时监控功能 4、具备语音识别、语音提醒功能 5、具备实时采集各种股票交易等相关数据的功能 6、已采集3000多只股票有史以来所有交易数据及分红配股数据 7、具备自主学习,辅助决策功能 8、具备买卖点计算功能,实测结果相当精准
LeetCode:2617. 网格图中最少访问的格子数(优先级队列 Java)
目录 2617. 网格图中最少访问的格子数 题目描述: 实现代码与解析: 优先级队列 原理思路: 2617. 网格图中最少访问的格子数 题目描述: 给你一个下标从 0 开始的 m x n 整数矩阵 grid 。你一开始的位置在 左上角 格子 (0, 0) 。 当你在格子 (i, j) 的时候,你可以移动到以下格子之一: 满足 j < k <= gri
树状数组优化dp,2617. 网格图中最少访问的格子数
目录 一、题目 1、题目描述 2、接口描述 3、原题链接 二、解题报告 1、思路分析 2、复杂度 3、代码详解 一、题目 1、题目描述 给你一个下标从 0 开始的 m x n 整数矩阵 grid 。你一开始的位置在 左上角 格子 (0, 0) 。 当你在格子 (i, j) 的时候,你可以移动到以下格子之一: 满足 j < k <= grid[i][j] + j
按面积筛选填充二值图中的孔洞-python源码
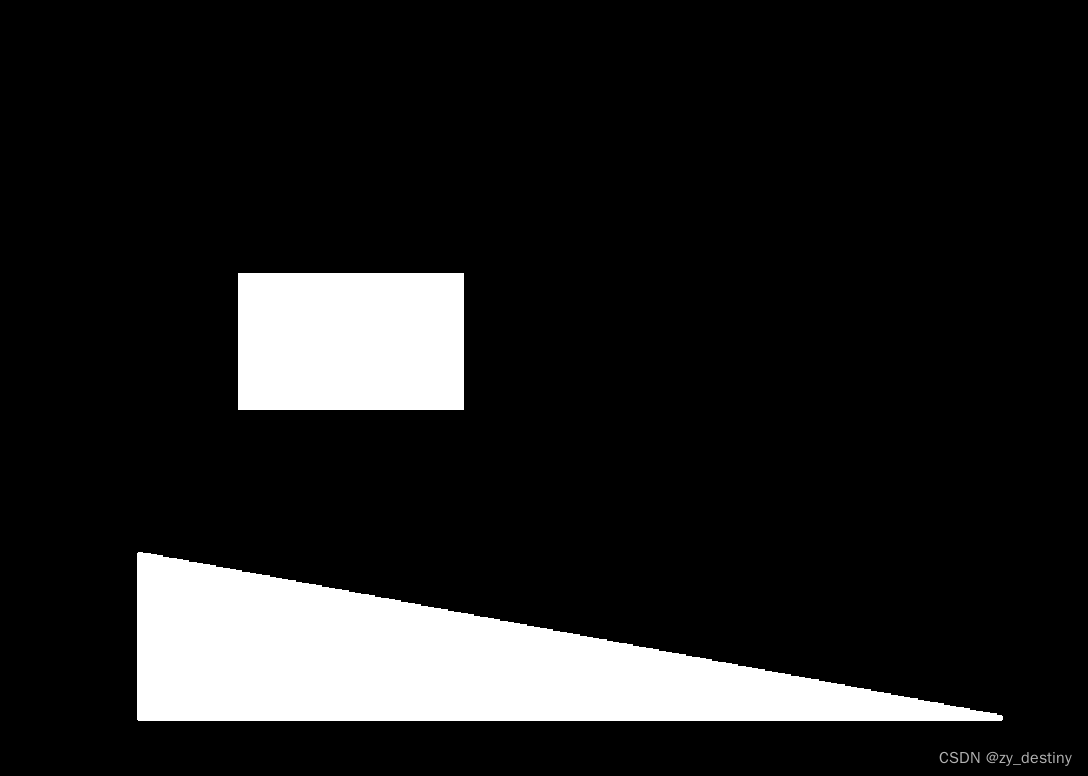
目录 🙋🙋需求 🍅🍅解决方案 🙋🙋需求 前提条件是二值图中0是背景,255是前景。 二值化后的影像中有很多小孔洞,现在需要按孔洞面积进行筛选,填充面积小于阈值的孔洞,面积太大的孔洞不需要填充。 输入图如下,需要填充椭圆形和五角星,矩形和三角形面积较大不填充: 🍅🍅解决方案
算法-计算无向图中两个节点之间所有的路径
1、深度优先遍历 1.1 深度优先遍历的定义 深度优先搜索(Depth_First Search)遍历类似于树的先根遍历,是树的先根遍历的推广。 假设给定图G,图中所有顶点未曾被访问过,则深度优先搜索可以从图中某个顶点v出发,访问此顶点,然后依次从v的未被访问的邻接点出发深度优先遍历图,直至图中所有和v有路径相通的顶点都被访问到;若此时图中尚有顶点未被访问,则另选图中一个未曾
011集——vba获取CAD图中图元类名objectname
在CAD中,通过快捷键PL(即POLYLINE命令)绘制的线属于AcDbPolyline。AcDbPolyline也被称为LWPOLYLINE,即简单Polyline,它所包含的对象在本身内部。 此外,CAD中还有另一种二维多段线对象,称为AcDb2dPolyline(也被称为POLYLINE)。这是一个复杂的实体,所包含的对象并不在本身内部,而是独立的点对象