四十三天专题

代码随想录算法训练营四十三天|1143.最长公共子序列、1035.不相交的线、53.最大子序和、392.判断子序列

题目链接：1143. 最长公共子序列 - 力扣（LeetCode）思路：如果text1[i - 1] 与 text2[j - 1]相同，那么找到了一个公共元素，所以dp[i][j] = dp[i - 1][j - 1] + 1; 如果text1[i - 1] 与 text2[j - 1]不相同，那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列和 t

Java重修笔记第四十三天 Set 集合、HashSet 类

Set 接口 1. 它是无序的（添加和取出的顺序不一致，但取出的结果是固定的），没有索引 2. Set 接口也是 Collection 的子接口，所以继承了 Collection 的方法 3. Set 接口的遍历方式有两种，迭代器和增强 for 循环，但是不能使用索引遍历 HashSet 类 1. 底层是一个 HashMap，可以把 HashSet 看成 HashMap 2

【代码随想录算法训练营第四十三天|卡码网52.携带研究材料、18.零钱兑换II、377.组合总和Ⅳ、卡码网57.爬楼梯】

文章目录卡码网52.携带研究材料518.零钱兑换II377.组合总和Ⅳ卡码网57.爬楼梯卡码网52.携带研究材料这题是完全背包问题，完全背包问题在01背包问题的基础上其实主要是三个不同，第一个是初始化的时候不能再和01背包一样对第一个物品让背包大小大于物品重量的时候全部初始化为物品价值，因为现在的物品可以无限放。第二个就是动态规划内部的循环推导的时候不用倒序而是正序了，因为

代码随想录算法训练营第四十三天 | 完全背包理论基础、518.零钱兑换II、377. 组合总和 Ⅳ、70. 爬楼梯（进阶）

完全背包理论基础题目链接：https://kamacoder.com/problempage.php?pid=1052 文档讲解：https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F… 视频讲解：https://www.bilibili.com/video/BV1uK41

代码随想录算法训练营第四十三天|LeetCode518 零钱兑换Ⅱ、LeetCode377 组合总和Ⅳ

01背包与完全背包： 01背包与完全背包最大的区别在于01背包物品每个只能取一次而完全背包每个物品可以取无数次，这也就导致了我们内层for循环中的不同。具体体现为：因为01背包每个物品仅用一次，所以我们将背包从大到小(倒序)遍历；而完全背包是可以多次添加那么需要将背包从小到大(正序)遍历。题1：指路：518. 零钱兑换 II - 力扣（LeetCode）思路与代码：凑金币，典型的

代码随想录算法训练营第四十三天| 377. 组合总和 Ⅳ、57. 爬楼梯（第八期模拟笔试）、322. 零钱兑换、279. 完全平方数

[LeetCode] 377. 组合总和 Ⅳ[LeetCode] 377. 组合总和 Ⅳ 文章解释 [LeetCode] 377. 组合总和 Ⅳ 视频解释题目：给你一个由不同整数组成的数组 nums ，和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。题目数据保证答案符合 32 位整数范围。示例 1：输入：nu

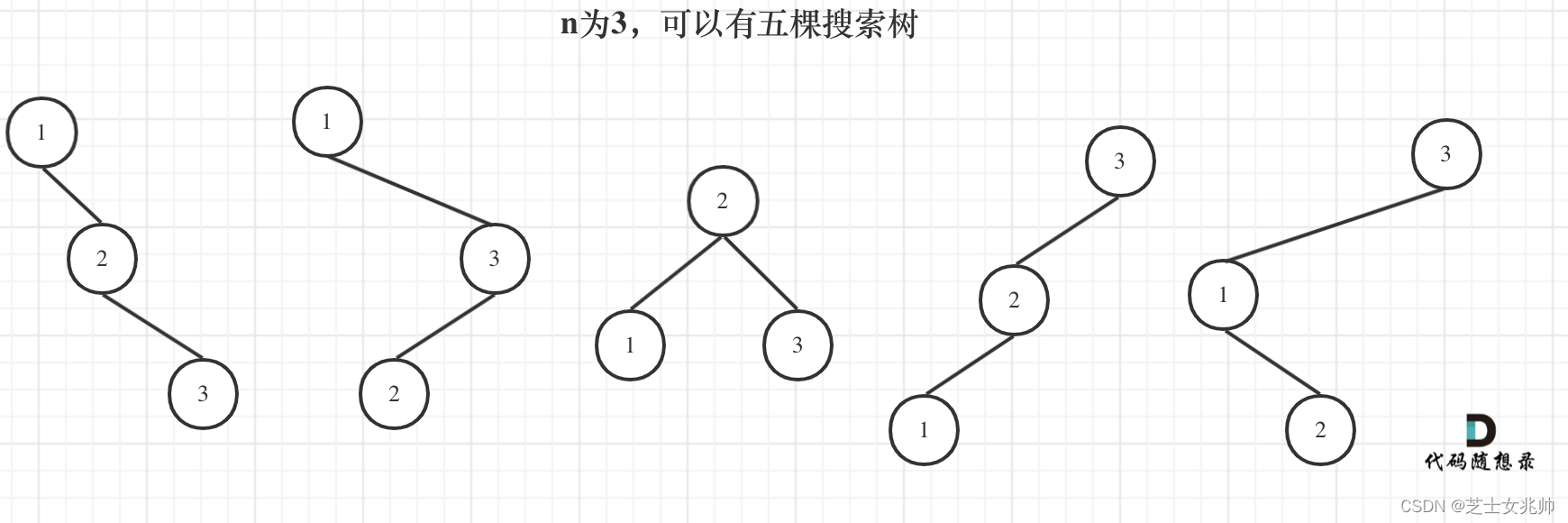
代码随想录算法训练营第四十三天 | 343. 整数拆分、96.不同的二叉搜索树

343. 整数拆分代码随想录视频讲解：动态规划，本题关键在于理解递推公式！| LeetCode：343. 整数拆分_哔哩哔哩_bilibili 解题思路 1. dp[i]对i进行拆分，得到的最大的乘积为dp[i] 2.递推公式一个是j * (i - j) 直接相乘，拆为两个数一个是j * dp[i - j]，相当于是拆分(i - j)，拆为三个或以上 dp[

代码随想录算法训练营第四十三天动态规划 part05● 1049. 最后一块石头的重量 II ● 494. 目标和 ● 474.一和零

1049. 最后一块石头的重量 II 题目链接： . - 力扣（LeetCode）思路：主要是要找到两个近似相等的子集和，去求这两个和的最小值; 之后就是和从子集中找相对应和的思路是一样的了注意点：1）dp 初始化；初始为 0； 2）j如果>= 当前物品的容量，是可以装进去的实现代码： var lastStoneWeightII = function (stones) {let su

代码随想录算法训练营第四十三天|1049. 最后一块石头的重量 II、494. 目标和、474.一和零

1049. 最后一块石头的重量 II 思路：本题其实就是尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，这样就化解成01背包问题了。是不是感觉和昨天讲解的416. 分割等和子集 (opens new window)非常像了。本题物品的重量为stones[i]，物品的价值也为stones[i]。对应着01背包里的物品重量weight[i]和物品价值value[i]。接下

学习java第四十三天

Spring AOP相关术语（1）切面（Aspect）：切面是通知和切点的结合。通知和切点共同定义了切面的全部内容。（2）连接点（Join point）：指方法，在Spring AOP中，一个连接点总是代表一个方法的执行。连接点是在应用执行过程中能够插入切面的一个点。这个点可以是调用方法时、抛出异常时、甚至修改一个字段时。切面代码可以利用这些点插入到应用的正常流程之中，并添加新的行为。

【动态规划】代码随想录算法训练营第四十三天 |1049. 最后一块石头的重量 II，494. 目标和，474.一和零（待补充）

1049. 最后一块石头的重量 II 1、题目链接：. - 力扣（LeetCode） 2、文章讲解：代码随想录 3、题目：有一堆石头，每块石头的重量都是正整数。每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：如果 x == y，那么两块石头都会被完全粉碎；如果 x != y，那么重量为 x 的石头

第四十三天| 1049. 最后一块石头的重量 II、494. 目标和、474.一和零

01背包问题 Leetcode 1049. 最后一块石头的重量 II 题目链接：1049 最后一块石头的重量 II 题干：有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：如果 x == y，那么两块石头都会被完

代码随想录算法训练营第四十三天|1049.最后一块石头的重量II、494.目标和

1049.最后一块石头的重量II public class Solution {public int LastStoneWeightII(int[] stones) {int sum=0;for(int i=0;i<stones.Length;i++){sum+=stones[i];}int target = sum / 2;int[] dp=new int [target+1];for(int

代码随想录训练营第三十期|第四十三天|动态规划 part05|1049. 最后一块石头的重量 II ● 494. 目标和 ● 474.一和零

1049. 最后一块石头的重量 II - 力扣（LeetCode） class Solution {public int lastStoneWeightII(int[] stones) {int sum = 0;for (int n : stones) {sum += n;}int target = sum / 2;int[] dp = new int[target + 1];for (int

代码随想录算法训练营第四十三天|1049. 最后一块石头的重量 II、494. 目标和、74. 一和零。

1049. 最后一块石头的重量 II 题目链接：最后一块石头的重量 II 题目描述：有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：如果 x == y，那么两块石头都会被完全粉碎；如果 x != y，那么

代码随想录算法训练营第四十三天| 1049. 最后一块石头的重量 II、494. 目标和、474.一和零

1049. 最后一块石头的重量 II 题目链接：力扣（LeetCode）官网 - 全球极客挚爱的技术成长平台解题思路：尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，这样就化解成01背包问题了。 java： class Solution {public int lastStoneWeightII(int[] stones) {int sum = 0;for (int i : sto

代码随想录算法训练营第四十三天 | 1049. 最后一块石头的重量 II、494. 目标和、474.一和零

01背包问题总结今天总结一下昨天的分割等和子集和今天三道题的的思路，都属于01背包问题。其实仔细观察就会发现，这四道题目本质上都是题目提供了一个集合，都需要在集合中选出满足目标的子集，且每个元素只能选一次，所以都是01背包问题。分割等和子集：不需要思路转换；石头：为了得到最小的石头，需要石头相撞，求出一个需要凑的子集，其和尽量接近整个集合求和的一半；目标和：加和减分别是子集，所以也是求子集，

算法随想录第四十三天打卡|1049. 最后一块石头的重量 II ，494. 目标和，474.一和零

1049. 最后一块石头的重量 II 本题就和昨天的 416. 分割等和子集很像了，可以尝试先自己思考做一做。视频讲解：动态规划之背包问题，这个背包最多能装多少？LeetCode：1049.最后一块石头的重量II_哔哩哔哩_bilibili 代码随想录 class Solution(object):def lastStoneWeightII(self, stones):total=s

代码随想录第四十三天——目标和，一和零

leetcode 494. 目标和题目链接：目标和本题要如何使表达式结果为target：既然为target，那么就一定有 left组合 - right组合 = target left + right = sum，而sum是固定的。right = sum - left，所以left - (sum - left) = target 推导出 left = (target + sum)/2 。此

代码随想录-刷题第四十三天

1049. 最后一块石头的重量 II 题目链接：1049. 最后一块石头的重量 II 思路：本题其实就是尽量让石头分成重量相同的两堆，相撞之后剩下的石头最小，这样就化解成0-1背包问题了。与416. 分割等和子集非常相似。动态规划五步曲： dp[j]：容量（其实就是重量）为j的背包，最多可以背最大重量为dp[j]。可以回忆一下0-1背包中，dp[j]的含义，容量为j的背包，最多可以

算法训练第四十三天|1049. 最后一块石头的重量 II、494. 目标和、474. 一和零

1049. 最后一块石头的重量 II：题目链接有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：如果 x == y，那么两块石头都会被完全粉碎；如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为

刷题第四十三天 309.买卖股票最佳时机+冷冻 714. 买卖股票最佳时机+手续费

class Solution:def maxProfit(self, prices: List[int]) -> int:#dp[i][0] 第i天持有股票手上的最大现金#dp[i][1] 第i天不持有股票，手上的最大现金#dp[i][0] = max(dp[i - 1][0], dp[i - 2][1] - prices[i]) 因为有一天冻结，并且无限次交易，所以第i天持有的情况之一就

刷题第四十三天 309.买卖股票最佳时机+冷冻 714. 买卖股票最佳时机+手续费

class Solution:def maxProfit(self, prices: List[int]) -> int:#dp[i][0] 第i天持有股票手上的最大现金#dp[i][1] 第i天不持有股票，手上的最大现金#dp[i][0] = max(dp[i - 1][0], dp[i - 2][1] - prices[i]) 因为有一天冻结，并且无限次交易，所以第i天持有的情况之一就

shell学习四十三天----临时性文件的建立与使用

临时性文件的建立与使用虽然使用管道可以省去建立临时性文件的需求,不过有时临时性文件还是派得上用场的.linux不同于其他的操作系统的地方就是:他没有那种将不再需要的文件设法删除的做法.反倒是提供了两个特殊目录:/tmp与/var/tmp(旧系统是/usr/tmp),这些文件可入场被存储,当他们未被清理干净时也不会弄乱一般的目录.大部分系统上的/tmp都会在系统开机时清理,不过/var/tmp下

算法随想录算法训练营第四十三天|300.最长递增子序列 674. 最长连续递增序列 718. 最长重复子数组

300.最长递增子序列题目：给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。子序列是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。 class Solution {public int lengthOfLIS(int[] nums) {int[] dp = new in