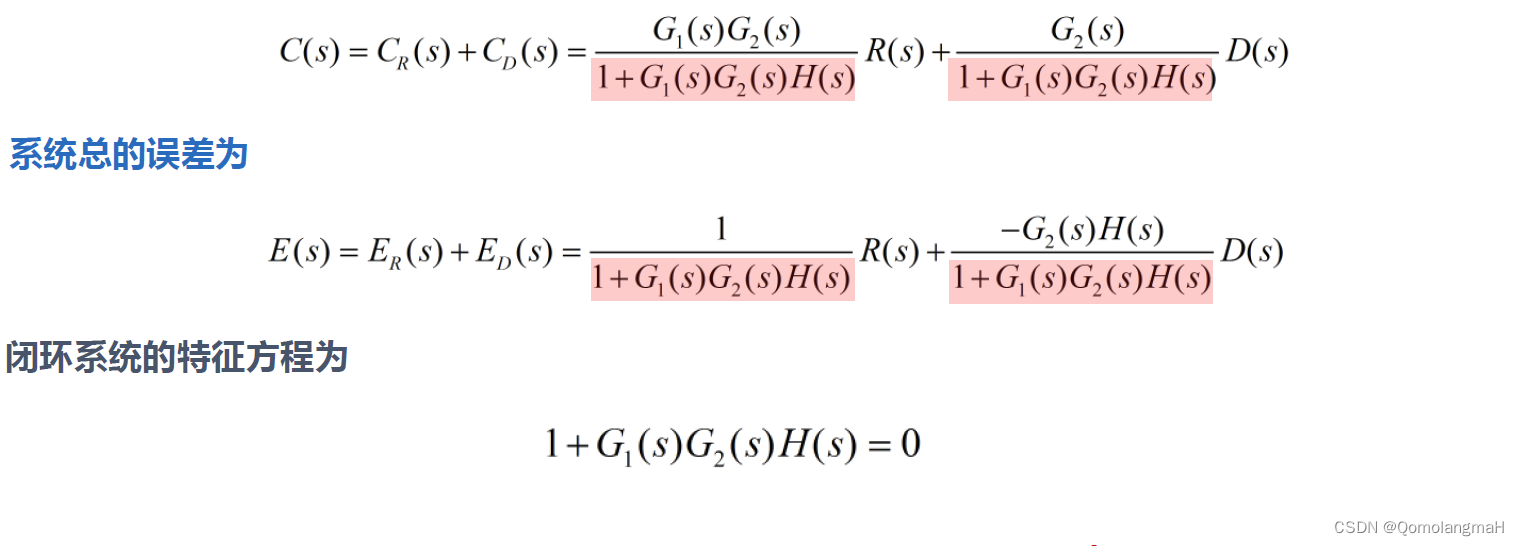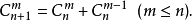化简专题
CCF CSP题解:因子化简(202312-2)
链接和思路 OJ链接:传送门。 问题重述 本题基于一个基本事实,即任何一个大整数 n n n都可以唯一地分解为如下形式 n = p 1 t 1 × p 2 t 2 × ⋯ × p m t m n = p_1^{t_1} \times p_2^{t_2} \times \cdots \times p_m^{t_m} n=p1t1×p2t2×⋯×pmtm其中, p 1 , p 2
【CSP】因子化简_(问题分析,过程拆解,方案构建)
一、问题背景与任务概述 在因子化简问题中,我们需要对给定的多个整数进行质因数分解,并根据题目要求的条件,计算出特定的因子并输出。这类问题在编程竞赛中十分常见,尤其是涉及大数处理时,如何高效地进行质因数分解并输出结果是一个关键点。 任务: 对每个输入的整数 n 进行质因数分解。根据质因数的分解结果,计算并输出满足条件的因子。 本文将通过详细的代码注释,逐步讲解如何实现这一任务,并分析其中的关
CCF-CSP真题《202312-2 因子化简》思路+python,c++满分题解
想查看其他题的真题及题解的同学可以前往查看:CCF-CSP真题附题解大全 试题编号:202312-2试题名称:因子化简时间限制:2.0s内存限制:512.0MB问题描述: 题目背景 质数(又称“素数”)是指在大于 1 的自然数中,除了 1 和它本身以外不再有其他因数的自然数。 问题描述 小 P 同学在学习了素数的概念后得知,任意的正整数 n 都可以唯一地表示为若干素因子相乘的形式。如果正整
matlab函数化简和函数极限
文章目录 化简求函数极限泰勒公式泰勒公式求解 化简 simplify 函数是MATLAB中符号计算工具箱提供的一个函数,用于简化数学表达式。它可以根据预定义的简化规则,对给定的数学表达式进行简化和转化。 以下是simplify 函数的一些常用用法: 简化表达式: simplify 函数可以对各种数学表达式进行简化,包括多项式、三角函数、指数函数等。例如,要简化表达式 si
因子化简——CSP认证题目
问题描述 小 P 同学在学习了素数的概念后得知,任意的正整数 n都可以唯一地表示为若干素因子相乘的形式。如果正整数 n有m 个不同的素数因子 p 1 , p 2 , … , p m p_1, p_2, \ldots, p_m p1,p2,…,pm,则可以表示为: n = p 1 t 1 ⋅ p 2 t 2 ⋅ p 3 t 3 ⋯ p m t m n = p_1^{t_1} \cdot p_
简单数学问题之分数的表示与化简
分数的化简 #include <iostream>#include <cmath>//调用abs函数using namespace std;int divide(int a,int b){if(b==0) return a;else return divide(b,a%b);}struct fraction{int up;//分子int down;//分母}result;fract
递推化简+线段树区间维护,P6477 [NOI Online #2 提高组] 子序列问题
一、题目 1.1题目背景 2s 512M 1.2题目描述 给定一个长度为 n n n 的正整数序列 A 1 A_1 A1, A 2 A_2 A2, ⋯ \cdots ⋯, A n A_n An。定义一个函数 f ( l , r ) f(l,r) f(l,r) 表示:序列中下标在 [ l , r ] [l,r] [l,r] 范围内的子区间中,不同的整数个数。换句话说, f
C语言中的指针变量p,特殊表达式p[0] ,(*p)[0],(px+3)[2] ,(*px)[3]化简方法
一.已知以下代码,请问以下 式子p[0] ,p[1] ,(*p)[0] ,(*p)[1] 是什么意思? int A[3] = {1,2,3};int (*p)[3] = &A; 因为前面的嵌入式C语言基础的章节中说过,数组下标其实就是数组首元素的地址往上偏移的单位数,即: *(A+0) 等价于 A[0]*(A+1) 等价于 A[1]*(A+2) 等价于 A
matlab 等式化简,Matlab化简表达式 多项式的操作步骤
亲们想知道Matlab化简表达式 多项式的操作吗?下面就是小编整理的Matlab化简表达式 多项式的操作步骤,赶紧来看看吧,希望能帮助到大家哦! Matlab化简表达式 多项式的操作步骤 相关指令简介 这儿介绍下采用公因子发简化表达式的相关置换指令。气质要的函数指令为:“subexpr”。subexpr是替换表达式命令。在很多特繁琐的解析表达式中,常有个在不同地方重复出现的表达式,此时用sim
matlab行列式化简,Matlab化简表达式多项式怎么操作?化简表达式及多项式教程详解...
亲们想知道Matlab化简表达式 多项式的操作吗?下面就是小编整理的Matlab化简表达式 多项式的操作步骤,赶紧来看看吧,希望能帮助到大家哦! Matlab化简表达式 多项式的操作步骤 相关指令简介 这儿介绍下采用公因子发简化表达式的相关置换指令。气质要的函数指令为:“subexpr”。subexpr是替换表达式命令。在很多特繁琐的解析表达式中,常有个在不同地方重复出现的表达式,此时用sim
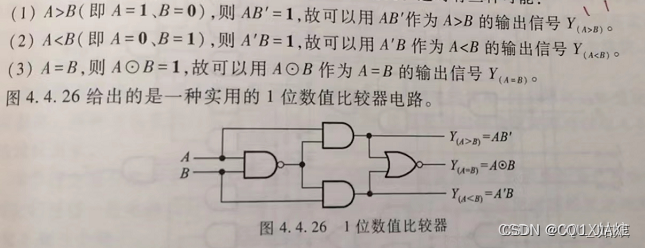
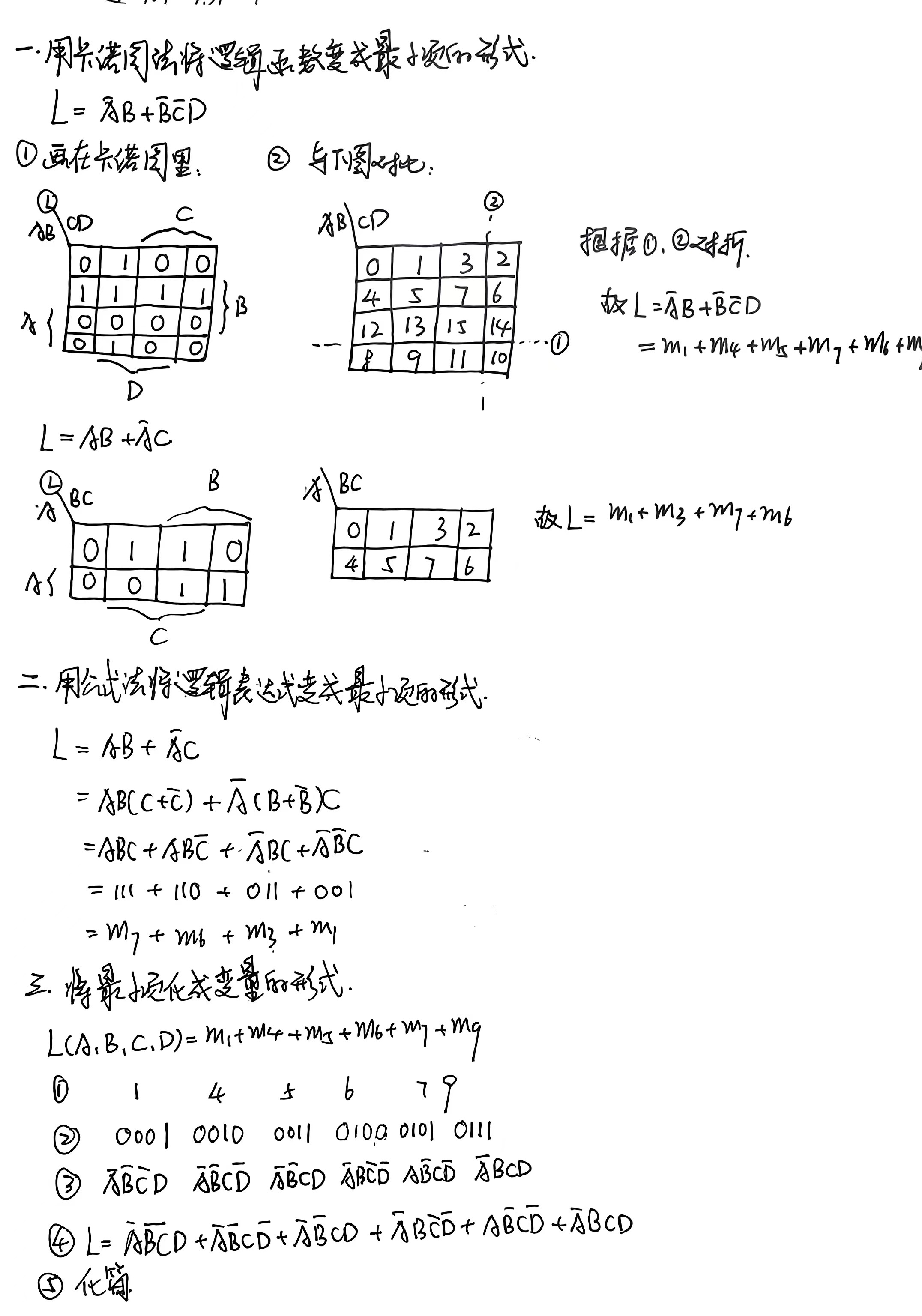
利用卡诺图对逻辑表达式进行化简
一、循环码 1. 循环码的定义 又称做格雷码。格雷码属于可靠性编码,是一种错误最小化的编码方式,因为,自然二进制码可以直接由数/模转换器转换成模拟信号,但某些情况,例如从十进制的3转换成4时二进制码的每一位都要变,使数字电路产生很大的尖峰电流脉冲。而格雷码则没有这一缺点,它是一种数字排序系统,其中的所有相邻整数在它们的数字表示中只有一个数字不同。它在任意两个相邻的数之间转换时,
Scala 集合类的应用【Map映射、filter过滤、化简、折叠、扫描、拉链、迭代器、stream流、View试图、并行集合、操作符】
文章目录 Map 映射的操作应用1. 实际需求2. 高阶函数解决实际需求3. 使用 map 映射来解决4. 模拟实现 map 函数机制5. flatmap 映射(扁平化) 集合元素过滤 filter化简(reduceLeft,reduceRight,reduce)折叠(foldLeft,foldRight)扫描(scanLeft,scanRight)综合案例拉链(zip 合并)迭代器 ite
12.12进制(原反补码,运算,进制转换),卡诺图化简,组合逻辑电路(竞争冒险,分析、设计方法),杂项
逻辑代数的基本定理和规则是用来处理逻辑函数的,其中包括以下几个重要的定理和规则: 1. 与门的性质: - 同一律:A∧A=A - 零律:A∧0=0 - 一律:A∧1=A 2. 或门的性质: - 同一律:A∨A=A - 零律:A∨0=A - 一律:A∨1=1 3. 非门的性质: - 否定律:¬(¬A)=A 4. 交换律: - 与门交换律:A∧B=B∧A - 或门交换律:A∨B=B∨A
【LeetCode】LCP 2. 分式化简
有一个同学在学习分式。他需要将一个连分数化成最简分数,你能帮助他吗? 连分数是形如上图的分式。在本题中,所有系数都是大于等于0的整数。 输入的cont代表连分数的系数(cont[0]代表上图的a0,以此类推)。返回一个长度为2的数组[n, m],使得连分数的值等于n / m,且n, m最大公约数为1。 示例 1: 输入:cont = [3, 2, 0, 2] 输出:[13,
奎恩-麦克拉斯基化简法 (Q-M 法)化简逻辑代数式
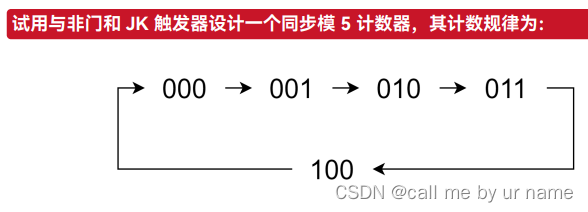
《数字电子技术基础(第6版)》(阎石) 极度暴力的模拟实现,不保熟的代码QAQ: #include<bits/stdc++.h>using namespace std;int n,m,cnt;vector<int>vec[11],temp;int a[100],head[11],tail[11],flag[1050];int box[1050][100],ans[100][100
数字逻辑笔记8丨2.6逻辑函数列表化简法
列表化简法的步骤 将函数表示成“最小项之和”的形式,并用二进制码表示每一个最小项作出质蕴涵项产生表,找出函数的全部质蕴涵项作出必要质蕴涵项产生表,找出函数的必要质蕴涵项当必要质蕴涵项不能覆盖所有最小项时,借助所需的质蕴涵项产生表,找出函数的最小覆盖 例子: 当给定函数的必要质蕴涵项集不能覆盖该函数的全部最小项时,还需进一步从剩余质蕴涵项集中找出所需质蕴涵项,以构成函数的最小质蕴涵
【自动控制原理】数学模型:系统框图及其化简、控制系统传递函数
文章目录 第2章 数学模型2.1 控制系统的运动微分方程2.2 拉氏变换和反变换2.3 传递函数2.4 系统框图2.4.1 系统框图2.4.2 系统框图的简化2.4.3 梅森公式2.4.4 例题答案解析——梅森公式 2.5 控制系统传递函数2.5.1 闭环系统的开环传递函数2.5.2 参考输入R(s)作用下的闭环传递函数2.5.3 扰动 D(s) 作用下的闭环传递函数2.5.4 当系统同时
GlobalMapper20化简矢量(降低顶点个数,降低数据体积)
序: 经常性的,我们需要一些矢量数据,来制作简单的专题图,但找到的矢量可能细节丰富,体积很大,导致操作很慢。这个时候就需要对矢量进行化简,因为我们只需要一个大致轮廓 此处以全国省界为例: 一、选中需要化简的对象 如果全部都需要化简,可以右键【Select-】 二、切换当前鼠标状态: 可以使用快捷键alt+D 三、在选中的对象上右键: 四、设置化简的阈值 多少米,删除掉
数字逻辑·时序线路设计【状态化简与编码】
化简原理 等价状态: 1、必要条件:在同样的输入作用下,有相同的输出 2、同样的输入条件下,相应的次态彼此等价 等价次态: 1、对应的次态相同 2、次态为两个现态本身或交错 3、两个次态为状态对封闭链中的一对 4、两个次态的某一后续状态对可以合并 等价状态具有可传递性:AB 等价,AC 等价= >BC 等价,则 A、B、C 为等价类 等价类:彼此等价的状态的集合 最大等价类:一个等价类不包含在任
c语言中18 4*3等于多少,数学符号c上4下8怎么算 可化简组合数的计算及证明与组...
导语:提到符号,大家应该都了解,有朋友问数学符号右上角逗号,另外,还有朋友想问五年级数学符号,这到底怎么回事呢?事实上c语言的运算符号定义呢,接下来小编在这里给大家带来数学符号c上4下8怎么算,一起来看看吧。 数学符号c上4下8怎么算 数学符号c右上角是1右下角是4的意思是数学中的组合,右下角的4表示总体个数,右上角的1表示抽取个数,且从4个里面抽取一个,C¹₄=4÷1=4。 组合:一般地,从





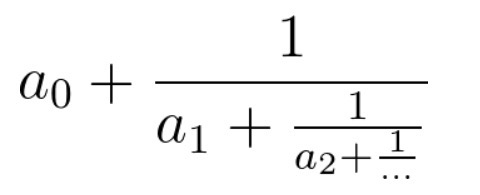
![C语言中的指针变量p,特殊表达式p[0] ,(*p)[0],(px+3)[2] ,(*px)[3]化简方法](https://img-blog.csdnimg.cn/direct/7aeae473c17248d59c1dc0d9f3377141.png)