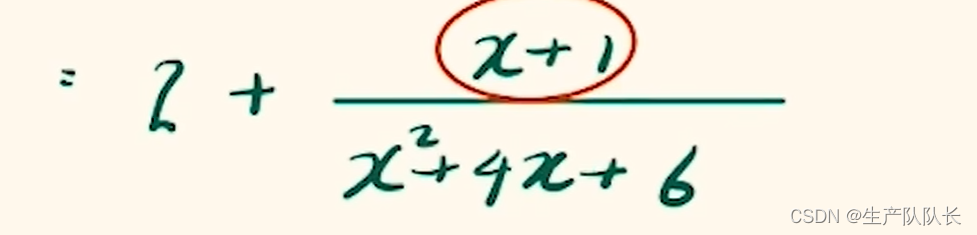2. 分式化简

本文主要是介绍2. 分式化简，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

最大公约数

注意：输出之间的分子分母不用交换

class Solution {
public:int gcd(int a, int b){if(b == 0) return a;return gcd(b, a%b);}vector<int> fraction(vector<int>& cont) {int t = 1;int n = cont.size();int u = cont[n-1];for(int i = n-2; i>= 0; i--){t += cont[i] * u;swap(u, t);}int g = gcd(u, t);return {u/g, t/g};}
};

这篇关于2. 分式化简的文章就介绍到这儿，希望我们推荐的文章对编程师们有所帮助！

---