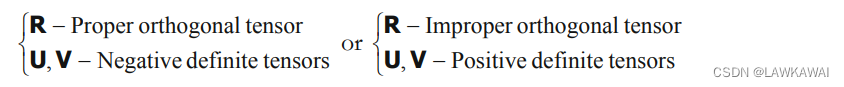力学专题
【会议征稿,JPCS出版】2024年航空航天与力学国际学术会议(ICAM 2024)
2024年航空航天与力学国际学术会议(ICAM 2024)将于2024年7月12-14日在中国沈阳举办。会议由东北大学机械工程与自动化学院主办,吉林大学机械与航空航天工程学院承办,大连理工大学、沈阳航空航天大学、沈阳建筑大学、沈阳工业大学、沈阳化工大学、东北电力大学协办。大会旨在为航空航天及相关力学领域的专家学者提供一个交流,学习的平台。大会诚邀国内外高校、科研机构专家、学者,企业界人士及其他相
【小呆的力学笔记】弹塑性力学的初步认知五:初始屈服条件(3)
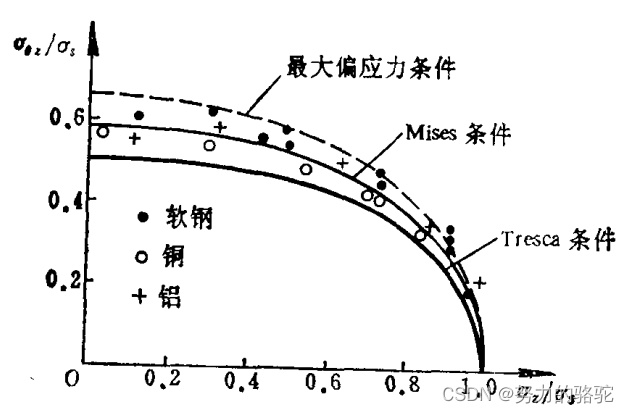
文章目录 3.7 屈服条件的实验验证一:薄圆管受拉力和内压的联合作用(Lode,1926年)3.8 屈服条件的实验验证二:薄圆管受拉力和扭矩的联合作用(Taylor-Quinney,1931) 上文中,提到了三种屈服条件:1. Tresca屈服条件(即第三强度理论),2. Mises屈服条件(即第四强度理论),3. 最大偏应力屈服条件(即第一强度理论的修正版),那么这三种屈服条
【PINN物理信息网络】基于PINN物理信息网络求解固体力学问题(python)
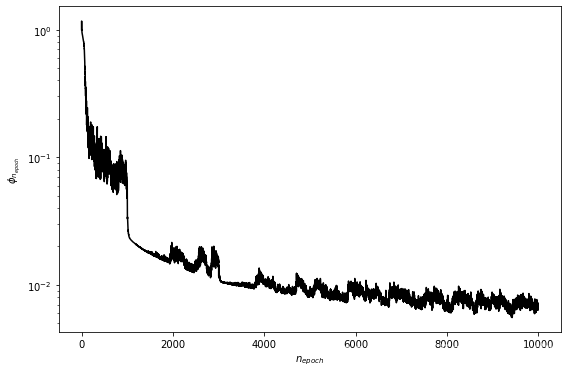
【PINN物理信息网络】基于PINN物理信息网络求解固体力学问题(python) 文章目录 【PINN物理信息网络】基于PINN物理信息网络求解固体力学问题(python)运行结果文章介绍基本步骤代码分享参考资料 运行结果
Comsol固体力学仿真﹣﹣受均匀内压的厚壁球壳弹塑性分析(加载卸载全流程)
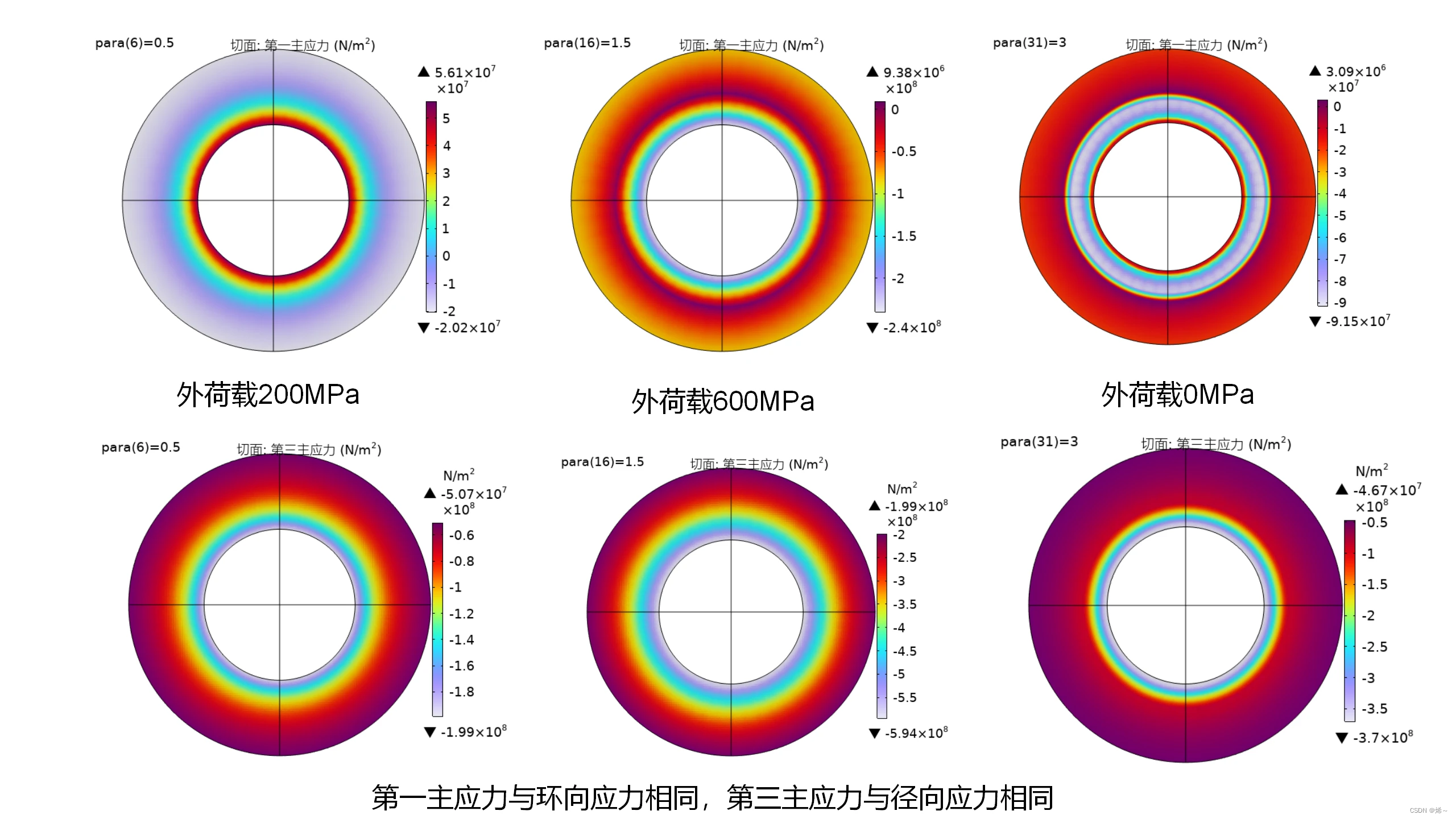
《弹塑性力学》大作业,记录一下。 COMSOL固体力学及结构力学仿真较少,故而查询了有关资料,才建立了如下模型。 图1 球体的有限元网格模型 该有限元模型是通过扫掠而得的结构化网格。 图2 加载卸载全历程中的塑型区域变化 图3 加载卸载全历程中的位移应力变化 图4 加载卸载全历程中的冯米塞斯应力变化 图5 关键节点应力场与塑性区分布 图6 关键节
【连续介质力学】涉及积分的定理
涉及积分的定理 分部积分 分部积分: ∫ a b u ( x ) v ′ ( x ) d x = u ( x ) v ( x ) ∣ a b − ∫ a b v ( x ) u ′ ( x ) d x \int_a^bu(x)v'(x)dx=u(x)v(x)|_a^b-\int_a^bv(x)u'(x)dx ∫abu(x)v′(x)dx=u(x)v(x)∣ab−∫abv(x)u′(x)
Unity(第十八部)物理力学,碰撞,触发、关节和材质
1、重力 刚体组件 英文中文描述RigidBody刚体组件physics->rigidbody ,刚体组件使一个物体有了质量,重力等。,use gravity 勾选后,物体才会受到重力,会自动下落,取消勾选就不会。,,is kinematic 表示运动学刚体,此时物体质量为0,就不会受重力的影响。 1. 质量2. 阻力3. 角阻力4. 使用重力(取消后,只是不受重力影响,阻力等还是受影响的
AI学会理解物理力学,机器像人更进一步 | 清华学神在MIT新研究
问耕 发自 凹非寺量子位 出品 | 公众号 QbitAI 机器能自行理解我们这个物理世界的基本规则么?答案是能。 多年以来,麻省理工学院(MIT)的研究人员一直在寻求解释和复制人类智能,而他们最近的研究成果,是如何让AI智能体拥有认知世界的基本能力。 即:学会分辨不同的对象,以及推断它们如何受到物理作用力的影响。 这包括几个方面。首先是看到图片后,能脑补其中物体的三维形状;其次是判断物体的物理
【小呆的力学笔记】弹塑性力学的初步认知五:初始屈服条件(1)
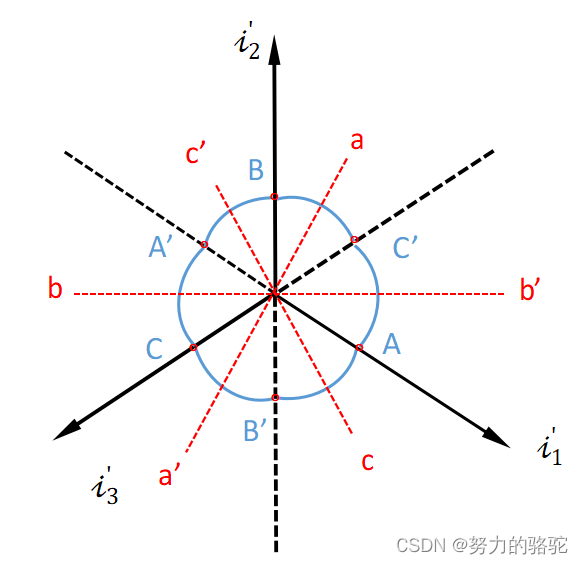
文章目录 3. 初始屈服条件3.1 两个假设以及屈服条件基本形式3.2 π \pi π平面、Lode参数3.3 屈服曲线的一般特征 3. 初始屈服条件 3.1 两个假设以及屈服条件基本形式 在简单拉伸时,材料的屈服很明确,即 σ > σ s (1) \sigma\gt\sigma_s\tag{1} σ>σs(1) 那么当一般应力状态下,材料的屈服条件是怎样的形式呢?
25天物理探索旅程 - 第二天:力学基石的构筑
第二天的课堂,我们将一起踏上一段力学世界的奇妙旅程,探索那些如同魔法般引导着宇宙万物运动法则的基石——牛顿三定律。想象一下,你手中握着一根魔杖,而那根魔杖正是我们今天要深入研究的力学奥秘:牛顿三大定律。别担心,这可不是霍格沃茨的黑魔法课,而是实实在在可以解释从苹果落地到火箭升空一切物理现象的“白魔法”课程。 首先,让我们以一种轻松且接地气的方式揭开牛顿第一定律(也被称为惯性定律)的神秘面纱。如
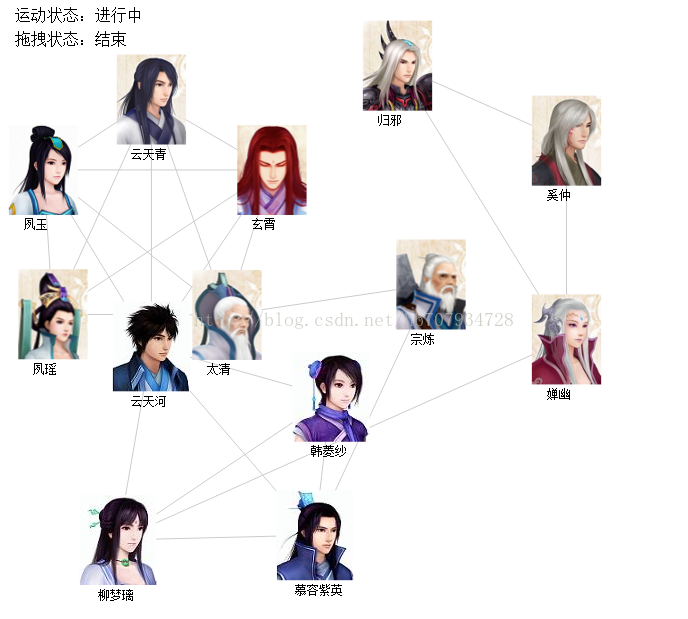
d3js实现力学图+人物关系图
描述人物关系的数据结构 {"nodes":[{ "name": "云天河" , "image" : "tianhe.png" },{ "name": "韩菱纱" , "image" : "lingsha.png" },{ "name": "柳梦璃" , "image" : "mengli.png" },{ "name": "慕容紫英" , "image"
Nature Commun.:物理所揭示原子分辨下的铁电涡旋畴的原位力学转变过程
通过复杂的晶格-电荷相互作用形成的铁电涡旋畴在纳米电子器件研发中具有巨大的应用潜力。实际应用中,如何在外界激励下操纵这类结构的拓扑状态是至关重要的。中国科学院物理研究所/北京凝聚态物理国家研究中心表面物理国家重点实验室与北京大学、湘潭大学和美国宾夕法尼亚大学研究团队合作,利用原子分辨的双球差矫正电镜,通过施加局部机械载荷操纵PbTiO3/SrTiO3超晶格中的涡旋。旋涡在外压应力作用下发生平面内极
【小呆的力学笔记】弹塑性力学的初步认知二:应力分析(1)
文章目录 1.1 一点的应力状态1.2 一点主应力状态1.3 应力偏张量、球张量、应力不变量 1.1 一点的应力状态 物体在受到外力或者自身不均匀的温度场等作用时,在其内部会产生内力,物体的内力与方向和截面都有关系。假设有一个受到外力作用的变形体,被一个平面截成A、B两个部分,B部分对A部分施加有作用力,在该截面上的dS微小面积上,作用力为dP,那么我们成dP与dS的比例极
专题2:弹性力学中平面问题的基本理论(2-6 物理方程 2-7 边界条件)
平面问题基本理论的核心内容到此就结束了,后面主要还剩一些寻找偏微分方程解析解的内容,这里就不再继续展示。因为建模是最核心最需要深刻理解的部分,而对于实际工程问题几乎不可能找到偏微分方程的解析解,都是用有限元的方法采用差分方程去逼近真实解。下面一篇内容将展示差分公式的推导,因为差分方程是最重要的得到数值解的方法。
与听力学有关的声音有哪些?
1.纯音(pure tone) 是单一的音。具有音高和响度两个基本特征。前者主要取决于声波的频率和波长,后者主要取决于声波的振幅。自然界很少有纯音。但在临床测听中常用纯音信号来检测不同频率听觉损失的程度。音叉和声波波信号发生器可产生不同波长的纯音。 2.泛音(Harmonics)是一种复合声音,简单地讲就是包含有纯音及与该纯音波长成整数分之一波长的声音。如1000Hz的纯音加上100
振动力学学习笔记: 理想元件(一) 弹性元件及其简化模型
前情提要 绪论(一) 振动力学的基本概念 绪论(二) 振动力学的基本问题与基本方法 绪论(三) 简谐振动及其三角函数、矢量、复数表示法 目 录 弹性元件基本属性常见弹性杆件的刚度公式推导拉压杆件悬臂梁简支梁扭转杆件 等效刚度的计算并联刚度串联刚度串并联的综合能量法 参考文献 在振动系统中,只有质量及其分布、运动阻尼、恢复力特性 等少数参数对振动特性及其响应起主导作用,对应
数理基础之轨道力学的三体问题,了解如何推导轨道力学中研究最多的问题(用于设计 James Webb 太空望远镜轨道)...
三体问题 让我们首先了解什么是三体问题。三体问题(或 3BP)是更广泛的n体问题的特例,它涉及预测天体在彼此引力影响下的运动。与更简单的二体问题 (2BP) 不同,三体问题没有封闭形式的解。这意味着必须使用初始条件(位置和速度)和数值方法来估计物体的运动。对于实际应用,3BP 可以专注于围绕两个较大质量(也称为初选)运行的卫星的运动;这些可能是卫星、行星或恒星。 一颗卫星在两个较
Blender源码探究之布料解算(三)——力学探索
花了一些时间,找到了布料解算中非常重要的一个部分,就是计算力的方法。 在这个cloth_calc_force方法内,对布料受到的各种外力几乎都考虑进去了。 如下图所示: 有重力、阻力、压力、风力、弹簧力 重力 很明显可以看到它把重力加速度算进去了 阻力 这个drag参数代表自于空气粘度阻力 由下面可以看出 粘度阻力计算
全国周培源大学生力学竞赛考试范围
下面是以前的参考范围: 理论力学 一、基本部分 (一) 静力学 (1) 掌握力、力矩和力系的基本概念及其性质。能熟练地计算力的投影、力对点的矩和力对轴的矩。 (2) 掌握力偶、力偶矩和力偶系的基本概念及其性质。能熟练地计算力偶矩及其投影。 (3) 掌握力系的主矢和主矩的基本概念及其性质。掌握汇交力系、平行力系与一般力系的简化方法、熟悉简化结果。能熟练地计算各类力系的主矢和主矩。掌握重
【连续介质力学】张量的范数、各向同性和各向异性张量、同轴张量和极分解
张量的范数 张量的大小,使用Frobenius 范数: ∣ ∣ v ⃗ ∣ ∣ = v ⃗ ⋅ v ⃗ = v i v i (向量) ||\vec v|| = \sqrt{\vec v \cdot \vec v} = \sqrt{v_iv_i} (向量) ∣∣v ∣∣=v ⋅v =vivi (向量) ∣ ∣ T ∣ ∣ = T : T = T i j T i j