本文主要是介绍【小呆的力学笔记】弹塑性力学的初步认知五:初始屈服条件(3),希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
文章目录
- 3.7 屈服条件的实验验证一:薄圆管受拉力和内压的联合作用(Lode,1926年)
- 3.8 屈服条件的实验验证二:薄圆管受拉力和扭矩的联合作用(Taylor-Quinney,1931)
上文中,提到了三种屈服条件:1. Tresca屈服条件(即第三强度理论),2. Mises屈服条件(即第四强度理论),3. 最大偏应力屈服条件(即第一强度理论的修正版),那么这三种屈服条件哪个更能贴近物理实际呢?历史上,有两个著名的验证屈服条件的试验,具体如下。
3.7 屈服条件的实验验证一:薄圆管受拉力和内压的联合作用(Lode,1926年)
试验的示意图如下图7所示,薄壁圆管的半径为 R R R,壁厚为 h h h,并且 h ≪ R h\ll R h≪R(至多1/20),其中薄壁圆管受内压 p p p和端面拉力T的联合作用,那么,取薄壁微元做应力分析如图8。

图 7 试验示意图 图7\quad试验示意图 图7试验示意图
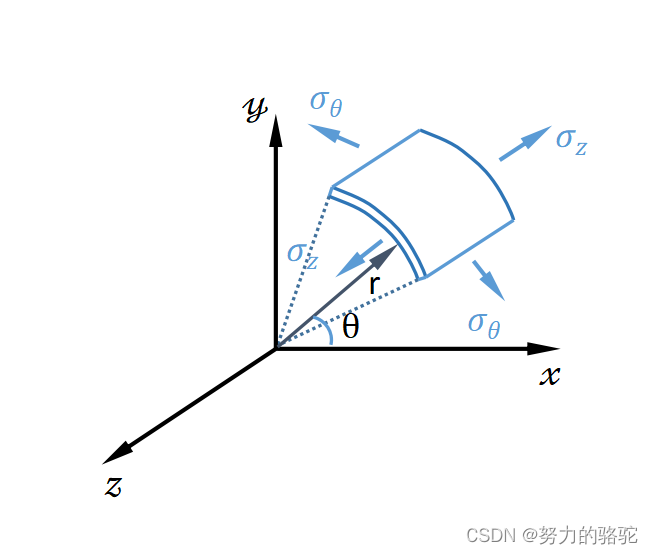
图 8 薄壁微元示意图 图8\quad薄壁微元示意图 图8薄壁微元示意图
由于薄壁圆管内外表面是自由表面,所以 τ r z = τ r θ = 0 \tau_{rz}=\tau_{r\theta}=0 τrz=τrθ=0。
极坐标系下的圆筒平衡方程如下式
∂ σ r ∂ r + 1 r ∂ τ r θ ∂ θ + σ r − σ θ r + f r = 0 1 r ∂ σ θ ∂ θ + ∂ τ r θ ∂ r + 2 τ r θ r + f θ = 0 (40) \begin{aligned} &\frac{\partial\sigma_r}{\partial r}+\frac{1}{r}\frac{\partial\tau_{r\theta}}{\partial\theta}+\frac{\sigma_r-\sigma_{\theta}}{r}+f_{r}=0\\ &\frac{1}{r}\frac{\partial\sigma_{\theta}}{\partial \theta}+\frac{\partial\tau_{r\theta}}{\partial r}+\frac{2\tau_{r\theta}}{r}+f_{{\theta}}=0 \end{aligned}\tag{40} ∂r∂σr+r1∂θ∂τrθ+rσr−σθ+fr=0r1∂θ∂σθ+∂r∂τrθ+r2τrθ+fθ=0(40)
当体力为零时,用应力函数 ϕ \phi ϕ表示的应力
σ r = 1 r ∂ ϕ ∂ r + 1 r 2 ∂ 2 ϕ ∂ θ 2 σ θ = ∂ 2 ϕ ∂ r 2 τ r θ = − ∂ ∂ r ( 1 r ∂ ϕ ∂ θ ) = 1 r 2 ∂ ϕ ∂ θ − 1 r ∂ 2 ϕ ∂ r θ (41) \begin{aligned} &\sigma_r=\frac{1}{r}\frac{\partial\phi}{\partial r}+\frac{1}{r^2}\frac{\partial^2\phi}{\partial {\theta}^2}\\ &\sigma_{\theta}=\frac{\partial^2\phi}{\partial r^2}\\ &\tau_{r\theta}=-\frac{\partial}{\partial r}(\frac{1}{ r}\frac{\partial \phi}{\partial \theta })=\frac{1}{r^2}\frac{\partial\phi}{\partial \theta}-\frac{1}{r}\frac{\partial^2\phi}{\partial r\theta} \end{aligned}\tag{41} σr=r1∂r∂ϕ+r21∂θ2∂2ϕσθ=∂r2∂2ϕτrθ=−∂r∂(r1∂θ∂ϕ)=r21∂θ∂ϕ−r1∂rθ∂2ϕ(41)
应力相容方程:
( ∂ 2 ∂ r 2 + 1 r ∂ ∂ r + 1 r 2 ∂ 2 ∂ θ 2 ) 2 ϕ = 0 (42) (\frac{\partial^2}{\partial r^2}+\frac{1}{ r}\frac{\partial}{\partial r}+\frac{1}{ r^2}\frac{\partial^2}{\partial {\theta}^2})^2\phi=0\tag{42} (∂r2∂2+r1∂r∂+r21∂θ2∂2)2ϕ=0(42)
在本试验中,结构和载荷都是轴对称的,因此应力函数 ϕ \phi ϕ只是径向坐标 r r r的函数,因此式(41)变为
σ r = 1 r ∂ ϕ ∂ r σ θ = ∂ 2 ϕ ∂ r 2 τ r θ = 0 (43) \begin{aligned} &\sigma_r=\frac{1}{r}\frac{\partial\phi}{\partial r}\\ &\sigma_{\theta}=\frac{\partial^2\phi}{\partial r^2}\\ &\tau_{r\theta}=0 \end{aligned}\tag{43} σr=r1∂r∂ϕσθ=∂r2∂2ϕτrθ=0(43)
同时式(42)变为
( ∂ 2 ∂ r 2 + 1 r ∂ ∂ r ) 2 ϕ = 0 (44) (\frac{\partial^2}{\partial r^2}+\frac{1}{ r}\frac{\partial}{\partial r})^2\phi=0\tag{44} (∂r2∂2+r1∂r∂)2ϕ=0(44)
上式为四节常微分方程,通解为
ϕ = A ln r + B r 2 ln r + C r 2 + D (45) \phi=A\ln r+Br^2\ln r+Cr^2+D\tag{45} ϕ=Alnr+Br2lnr+Cr2+D(45)
应力分量即为
σ r = A r 2 + B ( 1 + 2 ln r ) + 2 C σ θ = − A r 2 + B ( 3 + 2 ln r ) + 2 C τ r θ = 0 (46) \begin{aligned} &\sigma_r=\frac{A}{r^2}+B(1+2\ln r)+2C\\ &\sigma_{\theta}=-\frac{A}{r^2}+B(3+2\ln r)+2C\\ &\tau_{r\theta}=0 \end{aligned}\tag{46} σr=r2A+B(1+2lnr)+2Cσθ=−r2A+B(3+2lnr)+2Cτrθ=0(46)
极坐标下的几何方程和物理方程为
几何方程: ε r = ∂ u r ∂ r ε θ = u r r + 1 r ∂ u θ ∂ θ γ r θ = 1 r ∂ u r ∂ θ + ∂ u θ ∂ r − u θ r (47) 几何方程:\begin{aligned} &\varepsilon_r=\frac{\partial u_r}{\partial r}\\ &\varepsilon_{\theta}=\frac{u_r}{r}+\frac{1}{r}\frac{\partial u_\theta}{\partial \theta}\\ &\gamma_{r\theta}=\frac{1}{r}\frac{\partial u_r}{\partial \theta}+\frac{\partial u_\theta}{\partial r}-\frac{u_\theta}{ r} \end{aligned}\tag{47} 几何方程:εr=∂r∂urεθ=rur+r1∂θ∂uθγrθ=r1∂θ∂ur+∂r∂uθ−ruθ(47)
物理方程: ε r = 1 E ( σ r − μ σ θ ) ε θ = 1 E ( σ θ − μ σ r ) γ r θ = 2 ( 1 + μ ) E τ r θ (48) 物理方程:\begin{aligned} &\varepsilon_r= \frac{1}{E}(\sigma_r-\mu\sigma_\theta) \\ &\varepsilon_{\theta}= \frac{1}{E}(\sigma_\theta-\mu\sigma_r) \\ &\gamma_{r\theta}=\frac{2(1+\mu)}{E}\tau_{r\theta} \end{aligned}\tag{48} 物理方程:εr=E1(σr−μσθ)εθ=E1(σθ−μσr)γrθ=E2(1+μ)τrθ(48)
并且联立几何方程和物理方程,可得位移分量的形式解:
u r = 1 E [ − A r ( 1 + μ ) + 2 ( 1 − m u ) B r ( ln r − 1 ) + ( 1 − 3 μ ) B r + 2 C r ( 1 − μ ) ] + I cos θ + K sin θ u θ = 4 B r θ E + H r − I sin θ + K cos θ (49) \begin{aligned} u_r&=\frac{1}{E}[-\frac{A}{r}(1+\mu) +2(1-mu)Br(\ln r-1)+(1-3\mu)Br+2Cr(1-\mu) ]+I\cos\theta+K\sin\theta \\ u_\theta&=\frac{4Br\theta}{E}+Hr-I\sin\theta+K\cos\theta \end{aligned}\tag{49} uruθ=E1[−rA(1+μ)+2(1−mu)Br(lnr−1)+(1−3μ)Br+2Cr(1−μ)]+Icosθ+Ksinθ=E4Brθ+Hr−Isinθ+Kcosθ(49)
由位移的单值条件,有
u 0 = u 2 π = 0 → 4 B r ( 0 − 2 π ) E = 0 (50) \begin{aligned} u_0=u_{2\pi}=0\rightarrow\frac{4Br(0-2\pi)}{E}=0 \end{aligned}\tag{50} u0=u2π=0→E4Br(0−2π)=0(50)
那么 B = 0 B=0 B=0。
应力边界条件为
( σ r ) r = R = − p , ( σ r ) r = R + h = 0 (51) \begin{aligned} (\sigma_r)_{r=R}=-p,(\sigma_r)_{r=R+h}=0 \end{aligned}\tag{51} (σr)r=R=−p,(σr)r=R+h=0(51)
不难求得
σ r = − R 2 r 2 − 1 ( R + h ) 2 R 2 − 1 p , σ θ = R 2 r 2 + 1 ( R + h ) 2 R 2 − 1 p (52) \sigma_r=-\frac{\frac{R^2}{r^2}-1}{\frac{(R+h)^2}{R^2}-1}p,\sigma_\theta=\frac{\frac{R^2}{r^2}+1}{\frac{(R+h)^2}{R^2}-1}p\tag{52} σr=−R2(R+h)2−1r2R2−1p,σθ=R2(R+h)2−1r2R2+1p(52)
我们来看 σ r 、 σ θ \sigma_r、\sigma_\theta σr、σθ两者的大小对比
∣ σ θ σ r ∣ = R 2 r 2 + 1 ( R + h ) 2 R 2 − 1 ⋅ ( R + h ) 2 R 2 − 1 R 2 r 2 − 1 = R 2 r 2 + 1 1 − R 2 r 2 = R 2 + r 2 r 2 − R 2 = 1 + ( 1 + α ) 2 ( 1 + α ) 2 − 1 = 2 + 2 α + α 2 2 α + α 2 ≈ 2 + 2 α 2 α = 1 + 1 α (53) \begin{aligned} |\frac{\sigma_\theta}{\sigma_r}|&=\frac{\frac{R^2}{r^2}+1}{\frac{(R+h)^2}{R^2}-1}\cdot \frac{\frac{(R+h)^2}{R^2}-1}{\frac{R^2}{r^2}-1}\\ &=\frac{\frac{R^2}{r^2}+1}{1-\frac{R^2}{r^2}}\\ &=\frac{{R^2}+{r^2}}{{r^2}-{R^2}}=\frac{1+(1+\alpha)^2}{(1+\alpha)^2-1}=\frac{2+2\alpha+\alpha^2}{2\alpha+\alpha^2}\approx\frac{2+2\alpha}{2\alpha}=1+\frac{1}{\alpha} \end{aligned}\tag{53} ∣σrσθ∣=R2(R+h)2−1r2R2+1⋅r2R2−1R2(R+h)2−1=1−r2R2r2R2+1=r2−R2R2+r2=(1+α)2−11+(1+α)2=2α+α22+2α+α2≈2α2+2α=1+α1(53)
α ≪ 1 \alpha\ll1 α≪1,因此可以认为 σ r ≈ 0 \sigma_r\approx0 σr≈0
σ θ = R 2 r 2 + 1 ( R + h ) 2 R 2 − 1 p = R 2 ( R 2 r 2 + 1 ) 2 R h + h 2 p = R 2 ( R 2 ( 1 + α ) 2 R 2 + 1 ) 2 R ⋅ β R + ( β R ) 2 p = 1 ( 1 + α ) 2 + 1 2 β + β 2 p ≈ 1 β p = R h p (54) \begin{aligned} \sigma_\theta&=\frac{\frac{R^2}{r^2}+1}{\frac{(R+h)^2}{R^2}-1}p\\ &=\frac{R^2(\frac{R^2}{r^2}+1)}{2Rh+h^2}p\\ &=\frac{R^2(\frac{R^2}{(1+\alpha)^2R^2}+1)}{2R\cdot\beta R+(\beta R)^2}p\\ &=\frac{\frac{1}{(1+\alpha)^2}+1}{2\beta +\beta ^2}p\\ &\approx\frac{1}{\beta}p=\frac{R}{h}p \end{aligned}\tag{54} σθ=R2(R+h)2−1r2R2+1p=2Rh+h2R2(r2R2+1)p=2R⋅βR+(βR)2R2((1+α)2R2R2+1)p=2β+β2(1+α)21+1p≈β1p=hRp(54)
同时,薄壁圆管端面受拉力T,那么根据力平衡可得
σ z ⋅ [ π ( R + h ) 2 − π R 2 ] = σ z ⋅ ( 2 π R h + π h 2 ) ≈ σ z ⋅ 2 π R h = T (55) \sigma_z\cdot[\pi(R+h)^2-\pi R^2]=\sigma_z\cdot(2\pi Rh+\pi h^2)\approx\sigma_z\cdot 2\pi Rh=T\tag{55} σz⋅[π(R+h)2−πR2]=σz⋅(2πRh+πh2)≈σz⋅2πRh=T(55)
因此
σ θ ≈ P R h σ z ≈ T 2 π R h (56) \begin{aligned} &\sigma_{\theta}\approx\frac{PR}{h}\\ &\sigma_z\approx\frac{T}{2\pi Rh} \end{aligned}\tag{56} σθ≈hPRσz≈2πRhT(56)
假设载荷 p p p和T满足 σ θ ≥ σ z ≥ σ r \sigma_\theta\ge\sigma_z\ge\sigma_r σθ≥σz≥σr,则主应力为
σ 1 = σ θ , σ 2 = σ z , σ 3 = σ r = 0 (57) \sigma_1=\sigma_\theta,\sigma_2=\sigma_z,\sigma_3=\sigma_r=0\tag{57} σ1=σθ,σ2=σz,σ3=σr=0(57)
则有
μ σ = 2 σ 2 − σ 1 − σ 3 σ 1 − σ 3 = T − π R 2 p π R 2 p (58) \mu_\sigma=\frac{2\sigma_2-\sigma_1-\sigma_3}{\sigma_1-\sigma_3}=\frac{T-\pi R^2p}{\pi R^2p}\tag{58} μσ=σ1−σ32σ2−σ1−σ3=πR2pT−πR2p(58)
当T=0时, μ σ = − 1 \mu_\sigma=-1 μσ=−1,此时 θ σ = − 3 0 。 \theta_\sigma=-30^。 θσ=−30。,此时即为下图红圈,对应的就是材料的单向拉伸试验。
当 T = π R 2 p T=\pi R^2p T=πR2p时, μ σ = 0 \mu_\sigma=0 μσ=0,此时 θ σ = 0 。 \theta_\sigma=0^。 θσ=0。,此时即为下图x轴与屈服截面曲线的交点(绿色圈代表此时三种屈服条件)。
此时, σ θ = p R h , σ z = p R 2 h , σ r = 0 \sigma_\theta=\frac{pR}{h},\sigma_z=\frac{pR}{2h},\sigma_r=0 σθ=hpR,σz=2hpR,σr=0,如果减去静水应力 p R 2 h \frac{pR}{2h} 2hpR,那么 σ θ = p R 2 h , σ z = 0 , σ r = − p R 2 h \sigma_\theta=\frac{pR}{2h},\sigma_z=0,\sigma_r=-\frac{pR}{2h} σθ=2hpR,σz=0,σr=−2hpR,此时对应的就是材料的纯剪切试验。
当 T = 2 π R 2 p T=2\pi R^2p T=2πR2p时, μ σ = 1 \mu_\sigma=1 μσ=1,此时 θ σ = 3 0 。 \theta_\sigma=30^。 θσ=30。此时即为下图黄圈,对应的就是材料的单向压缩试验。
因此只要载荷满足 0 ≤ T ≤ 2 π R 2 p 0\le T\le 2\pi R^2p 0≤T≤2πR2p的范围内改变T和p,就可以得到 − 3 0 。 ∼ 3 0 。 -30^。\sim30^。 −30。∼30。的屈服曲线。
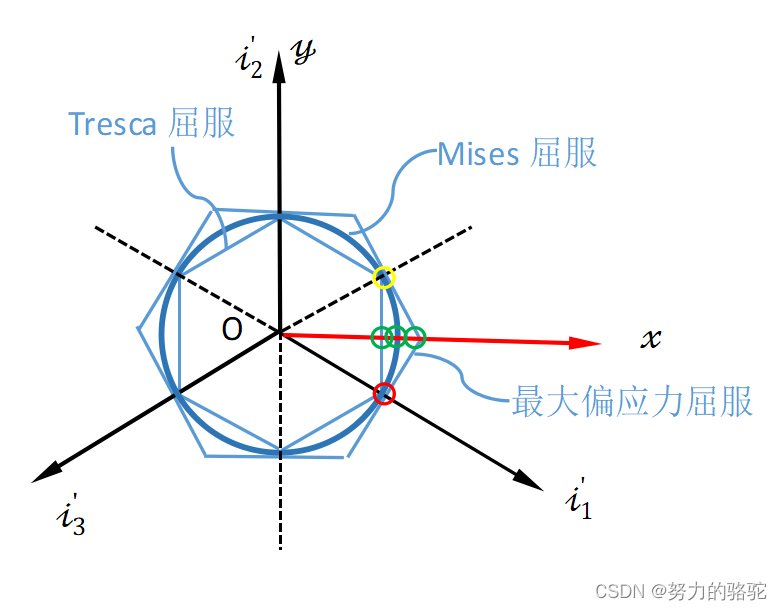
图 9 三种屈服条件 图9\quad三种屈服条件 图9三种屈服条件
Lode曾对铁、铜等材料进行了一系列试验,现在来对比三个屈服条件和试验的符合程度。
不失一般性,假设 σ 1 ≥ σ 2 ≥ σ 3 \sigma_1\ge\sigma_2\ge\sigma_3 σ1≥σ2≥σ3,那么对于Tresca屈服条件,有
σ 1 − σ 3 σ s = 1 (59) \frac{\sigma_1-\sigma_3}{\sigma_s}=1\tag{59} σsσ1−σ3=1(59)
对于Mises屈服条件 f ( σ i j ) = J 2 − k 2 2 = 1 3 σ s 2 − k 2 2 = 0 f(\sigma_{ij})=J_2-k_2^2=\frac{1}{3}\sigma_s^2-k_2^2=0 f(σij)=J2−k22=31σs2−k22=0
σ s = 3 k 2 = 3 J 2 = 3 ⋅ r σ 2 = 3 2 r σ = 3 2 x 2 + y 2 (60) \sigma_s=\sqrt3k_2=\sqrt3\sqrt{J_2}=\sqrt3\cdot\frac{r_\sigma}{\sqrt2}=\sqrt{\frac{3}{2}}r_\sigma=\sqrt{\frac{3}{2}}\sqrt{x^2+y^2}\tag{60} σs=3k2=3J2=3⋅2rσ=23rσ=23x2+y2(60)
其中x、y详见上章节
σ s = 3 2 x 2 + y 2 = 3 2 x 1 + ( y x ) 2 = 3 2 ⋅ σ 1 − σ 3 2 ⋅ 1 + ( μ σ 3 ) 2 \sigma_s=\sqrt{\frac{3}{2}}\sqrt{x^2+y^2}=\sqrt{\frac{3}{2}}x\sqrt{1+(\frac{y}{x})^2}=\sqrt{\frac{3}{2}}\cdot\frac{\sigma_1-\sigma_3}{\sqrt2}\cdot\sqrt{1+(\frac{\mu_\sigma}{\sqrt3})^2} σs=23x2+y2=23x1+(xy)2=23⋅2σ1−σ3⋅1+(3μσ)2
那么
σ 1 − σ 3 σ s = 2 3 ⋅ 1 1 + ( μ σ 3 ) = 2 3 + μ σ 2 (61) \frac{\sigma_1-\sigma_3}{\sigma_s}=\frac{2}{\sqrt3}\cdot\sqrt{\frac{1}{1+(\frac{\mu_\sigma}{\sqrt3})}}=\frac{2}{\sqrt{3+\mu_\sigma^2}}\tag{61} σsσ1−σ3=32⋅1+(3μσ)1=3+μσ22(61)
最后来看最大偏应力屈服条件,由假设 σ 1 ≥ σ 2 ≥ σ 3 \sigma_1\ge\sigma_2\ge\sigma_3 σ1≥σ2≥σ3,可得 s 1 ≥ s 2 ≥ s 3 s_1\ge s_2\ge s_3 s1≥s2≥s3,所以
μ σ = 2 σ 2 − σ 1 − σ 3 σ 1 − σ 3 = 3 s 2 s 1 − s 3 = − 3 ( s 1 + s 3 ) s 1 − s 3 (62) \mu_\sigma=\frac{2\sigma_2-\sigma_1-\sigma_3}{\sigma_1-\sigma_3}=\frac{3s_2}{s_1-s_3}=\frac{-3(s_1+s_3)}{s_1-s_3}\tag{62} μσ=σ1−σ32σ2−σ1−σ3=s1−s33s2=s1−s3−3(s1+s3)(62)
由上式可以求出
s 1 s 3 = μ σ − 3 μ σ + 3 (63) \frac{s_1}{s_3}=\frac{\mu_\sigma-3}{\mu_\sigma+3}\tag{63} s3s1=μσ+3μσ−3(63)
上一节内容中以及得到以下结论
s 1 = 2 3 σ s , − 1 ≤ μ σ ≤ 0 s 3 = − 2 3 σ s , 0 ≤ μ σ ≤ 1 s_1=\frac{2}{3}\sigma_s,-1\le\mu_\sigma\le0\\ s_3=-\frac{2}{3}\sigma_s,0\le\mu_\sigma\le1 s1=32σs,−1≤μσ≤0s3=−32σs,0≤μσ≤1
在 − 1 ≤ μ σ ≤ 0 -1\le\mu_\sigma\le0 −1≤μσ≤0时,
σ 1 − σ 3 σ s = s 1 − s 3 σ s = s 1 σ s ( 1 − s 3 s 1 ) = s 1 σ s ( 1 − μ σ + 3 μ σ − 3 ) = 4 3 − μ σ (64) \frac{\sigma_1-\sigma_3}{\sigma_s}=\frac{s_1-s_3}{\sigma_s}=\frac{s_1}{\sigma_s}(1-\frac{s_3}{s_1})=\frac{s_1}{\sigma_s}(1-\frac{\mu_\sigma+3}{\mu_\sigma-3})=\frac{4}{3-\mu_\sigma}\tag{64} σsσ1−σ3=σss1−s3=σss1(1−s1s3)=σss1(1−μσ−3μσ+3)=3−μσ4(64)
在 0 ≤ μ σ ≤ 1 0\le\mu_\sigma\le1 0≤μσ≤1时,
σ 1 − σ 3 σ s = s 1 − s 3 σ s = s 3 σ s ( s 1 s 3 − 1 ) = s 3 σ s ( μ σ − 3 μ σ + 3 − 1 ) = 4 3 + μ σ (65) \frac{\sigma_1-\sigma_3}{\sigma_s}=\frac{s_1-s_3}{\sigma_s}=\frac{s_3}{\sigma_s}(\frac{s_1}{s_3}-1)=\frac{s_3}{\sigma_s}(\frac{\mu_\sigma-3}{\mu_\sigma+3}-1)=\frac{4}{3+\mu_\sigma}\tag{65} σsσ1−σ3=σss1−s3=σss3(s3s1−1)=σss3(μσ+3μσ−3−1)=3+μσ4(65)
那么,在 − 1 ≤ μ σ ≤ 1 -1\le\mu_\sigma\le1 −1≤μσ≤1时, σ 1 − σ 3 σ s = 4 3 + ∣ μ σ ∣ (66) \frac{\sigma_1-\sigma_3}{\sigma_s}=\frac{4}{3+|\mu_\sigma|}\tag{66} σsσ1−σ3=3+∣μσ∣4(66)
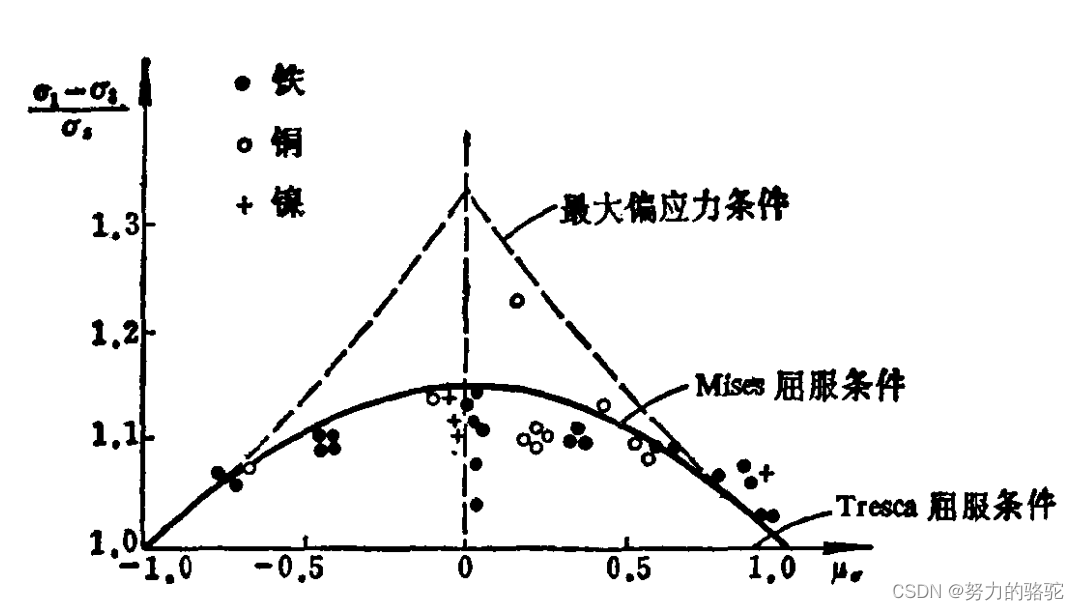
图 10 实验结果以及三种屈服条件 图10\quad实验结果以及三种屈服条件 图10实验结果以及三种屈服条件
将试验结果以及三种屈服条件绘制在一张图,如上图,不难发现实验结果更接近Mises屈服条件。同时可以发现所有结果都在Tresca屈服条件和最大偏应力条件中间,即Tresca屈服条件为下届,最大偏应力条件为上届。
3.8 屈服条件的实验验证二:薄圆管受拉力和扭矩的联合作用(Taylor-Quinney,1931)
试验的示意图如下图11所示,薄壁圆管的半径为 R R R,壁厚为 h h h,并且 h ≪ R h\ll R h≪R(至多1/20),其中薄壁圆管受端面拉力T和扭矩M的联合作用。

图 11 试验示意图 图11\quad试验示意图 图11试验示意图
对薄圆管在扭矩作用下进行的截面受力分析,示意图如下图12,那么不难得出
∫ 0 A τ z ⋅ d A ⋅ R = ∫ 0 2 π τ z R ⋅ ( R + h ) 2 − R 2 2 ⋅ d θ = τ z π R ⋅ ( ( R + h ) 2 − R 2 ) = M (67) \int_{0}^{A}\tau_z\cdot dA\cdot R=\int_{0}^{2\pi}\tau_zR\cdot \frac{(R+h)^2-R^2}{2}\cdot d\theta=\tau_z\pi R\cdot ((R+h)^2-R^2)=M\tag{67} ∫0Aτz⋅dA⋅R=∫02πτzR⋅2(R+h)2−R2⋅dθ=τzπR⋅((R+h)2−R2)=M(67)
由薄圆管的 h ≪ R h\ll R h≪R(至多1/20),可得
τ z = M π R ⋅ ( ( R + h ) 2 − R 2 ) = M π R ⋅ ( 2 R h + h 2 ) ≈ M 2 π R 2 h (68) \tau_z=\frac{M}{\pi R\cdot((R+h)^2-R^2)}=\frac{M}{\pi R\cdot(2Rh+h^2)}\approx\frac{M}{2\pi R^2h}\tag{68} τz=πR⋅((R+h)2−R2)M=πR⋅(2Rh+h2)M≈2πR2hM(68)
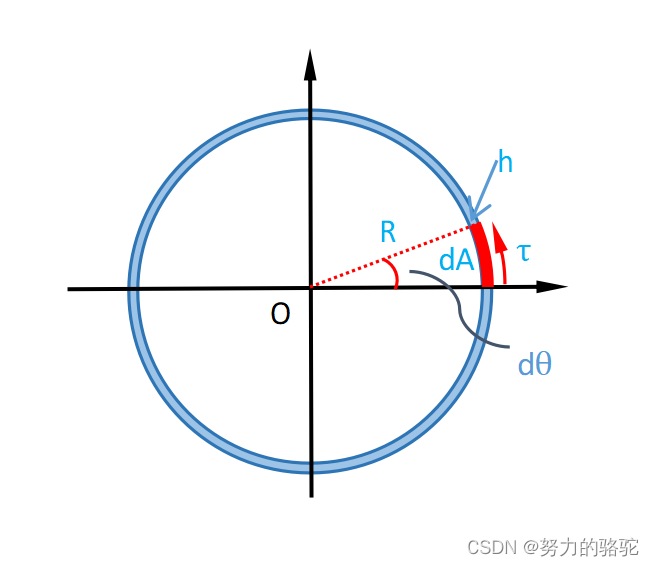
图 12 受力分析示意图 图12\quad受力分析示意图 图12受力分析示意图
薄壁圆管端面受拉力T,上文中已得到
σ z ⋅ [ π ( R + h ) 2 − π R 2 ] = σ z ⋅ ( 2 π R h + π h 2 ) ≈ σ z ⋅ 2 π R h = T \sigma_z\cdot[\pi(R+h)^2-\pi R^2]=\sigma_z\cdot(2\pi Rh+\pi h^2)\approx\sigma_z\cdot 2\pi Rh=T σz⋅[π(R+h)2−πR2]=σz⋅(2πRh+πh2)≈σz⋅2πRh=T
因此,在拉力T和扭矩M作用下,应力分量为
σ θ z ≈ M 2 π R 2 h σ z ≈ T 2 π R h (69) \begin{aligned} &\sigma_{\theta z}\approx\frac{M}{2\pi R^2h}\\ &\sigma_z\approx\frac{T}{2\pi Rh} \end{aligned}\tag{69} σθz≈2πR2hMσz≈2πRhT(69)
其应力张量近似为
[ 0 0 0 0 0 σ θ z 0 σ θ z σ z ] (70) \begin{bmatrix} 0 & 0 & 0\\ 0 & 0 & \sigma_{\theta z} \\0 & \sigma_{\theta z} & \sigma_z \end{bmatrix}\tag{70} 00000σθz0σθzσz (70)
那么其主应力为
σ 1 = σ z 2 + 1 2 σ z 2 + 4 σ θ z 2 σ 2 = 0 σ 3 = σ z 2 − 1 2 σ z 2 + 4 σ θ z 2 (71) \begin{aligned} &\sigma_1=\frac{\sigma_z}{2}+\frac{1}{2}\sqrt{\sigma_z^2+4\sigma_{\theta z}^2}\\ &\sigma_2=0\\ &\sigma_3=\frac{\sigma_z}{2}-\frac{1}{2}\sqrt{\sigma_z^2+4\sigma_{\theta z}^2} \end{aligned}\tag{71} σ1=2σz+21σz2+4σθz2σ2=0σ3=2σz−21σz2+4σθz2(71)
那么Lode参数为
μ σ = 2 σ 2 − σ 1 − σ 3 σ 1 − σ 3 = − σ z σ z 2 + 4 σ θ z 2 = − T T 2 + 4 M 2 / R 2 (72) \mu_\sigma=\frac{2\sigma_2-\sigma_1-\sigma_3}{\sigma_1-\sigma_3}=\frac{-\sigma_z}{\sqrt{\sigma_z^2+4\sigma_{\theta z}^2}}=\frac{-T}{\sqrt{T^2+4M^2/R^2}}\tag{72} μσ=σ1−σ32σ2−σ1−σ3=σz2+4σθz2−σz=T2+4M2/R2−T(72)
当 M = 0 M=0 M=0, T > 0 T\gt0 T>0时,这对应简单拉伸实验,此时 μ σ = − 1 \mu_\sigma=-1 μσ=−1。
当 T = 0 T=0 T=0, M ≠ 0 M\neq0 M=0时,这对应纯剪切实验,此时 μ σ = 0 \mu_\sigma=0 μσ=0。
改变T和M的比值,便可得到 − 1 ≤ μ σ ≤ 0 -1\le\mu_\sigma\le0 −1≤μσ≤0的各种应力状态。
Tresca屈服条件为
τ m a x = σ 1 − σ 3 2 = 1 2 σ z 2 + 4 σ θ z 2 = σ s 2 (73) \tau_{max}=\frac{\sigma_1-\sigma_3}{2}=\frac{1}{2}\sqrt{\sigma_z^2+4\sigma_{\theta z}^2}=\frac{\sigma_s}{2}\tag{73} τmax=2σ1−σ3=21σz2+4σθz2=2σs(73)
上式可变换成
( σ z σ s ) 2 + 4 ( σ θ z σ s ) 2 = 1 (74) (\frac{\sigma_z}{\sigma_s})^2+4(\frac{\sigma_{\theta z}}{\sigma_s})^2=1\tag{74} (σsσz)2+4(σsσθz)2=1(74)
Mises屈服条件为
J 2 − σ s 2 3 = 1 6 [ ( σ 1 − σ 2 ) 2 + ( σ 1 − σ 3 ) 2 + ( σ 2 − σ 3 ) 2 ] − σ s 2 3 = 0 (75) J_2-\frac{\sigma_s^2}{3}=\frac{1}{6}[(\sigma_1-\sigma_2)^2+(\sigma_1-\sigma_3)^2+(\sigma_2-\sigma_3)^2]-\frac{\sigma_s^2}{3}=0\tag{75} J2−3σs2=61[(σ1−σ2)2+(σ1−σ3)2+(σ2−σ3)2]−3σs2=0(75)
将式(71)代入上式
1 6 [ ( σ 1 − σ 2 ) 2 + ( σ 1 − σ 3 ) 2 + ( σ 2 − σ 3 ) 2 ] − σ s 2 3 = 1 6 [ σ 1 2 + ( σ 1 − σ 3 ) 2 + σ 3 2 ] − σ s 2 3 = 1 6 [ 2 ( σ z 2 ) 2 + 2 ( 1 2 σ z 2 + 4 σ θ z 2 ) 2 + ( σ z 2 + 4 σ θ z 2 ) 2 ] − σ s 2 3 = 1 6 ( 2 σ z 2 + 6 σ θ z 2 ) − σ s 2 3 = 0 (76) \begin{aligned} &\frac{1}{6}[(\sigma_1-\sigma_2)^2+(\sigma_1-\sigma_3)^2+(\sigma_2-\sigma_3)^2]-\frac{\sigma_s^2}{3}\\ =&\frac{1}{6}[\sigma_1^2+(\sigma_1-\sigma_3)^2+\sigma_3^2]-\frac{\sigma_s^2}{3}\\ =&\frac{1}{6}[2(\frac{\sigma_z}{2})^2+2(\frac{1}{2}\sqrt{\sigma_z^2+4\sigma_{\theta z}^2})^2+(\sqrt{\sigma_z^2+4\sigma_{\theta z}^2})^2]-\frac{\sigma_s^2}{3}\\ =&\frac{1}{6}(2\sigma_z^2+6\sigma_{\theta z}^2)-\frac{\sigma_s^2}{3}=0 \end{aligned}\tag{76} ===61[(σ1−σ2)2+(σ1−σ3)2+(σ2−σ3)2]−3σs261[σ12+(σ1−σ3)2+σ32]−3σs261[2(2σz)2+2(21σz2+4σθz2)2+(σz2+4σθz2)2]−3σs261(2σz2+6σθz2)−3σs2=0(76)
跟Tresca屈服条件一样,式(76)也可以变化为式(74)形式如下
( σ z σ s ) 2 + 3 ( σ θ z σ s ) 2 = 1 (77) (\frac{\sigma_z}{\sigma_s})^2+3(\frac{\sigma_{\theta z}}{\sigma_s})^2=1\tag{77} (σsσz)2+3(σsσθz)2=1(77)
最后看最大偏应力屈服条件,先看主偏应力应为
s 1 = σ z 6 + 1 2 σ z 2 + 4 σ θ z 2 s 2 = − σ z 3 s 3 = σ z 6 − 1 2 σ z 2 + 4 σ θ z 2 (78) \begin{aligned} &s_1=\frac{\sigma_z}{6}+\frac{1}{2}\sqrt{\sigma_z^2+4\sigma_{\theta z}^2}\\ &s_2=-\frac{\sigma_z}{3}\\ &s_3=\frac{\sigma_z}{6}-\frac{1}{2}\sqrt{\sigma_z^2+4\sigma_{\theta z}^2} \end{aligned}\tag{78} s1=6σz+21σz2+4σθz2s2=−3σzs3=6σz−21σz2+4σθz2(78)
那么最大偏应力屈服条件为
3 s 1 = 3 ( σ z 6 + 1 2 σ z 2 + 4 σ θ z 2 ) = 2 σ s (79) 3s_1=3(\frac{\sigma_z}{6}+\frac{1}{2}\sqrt{\sigma_z^2+4\sigma_{\theta z}^2})=2\sigma_s \tag{79} 3s1=3(6σz+21σz2+4σθz2)=2σs(79)
同样,上式也可以化为如下形式
1 4 ( σ z σ s ) + 3 4 ( σ z σ s ) 2 + 4 ( σ θ z σ s ) 2 = 1 (80) \frac{1}{4}(\frac{\sigma_z}{\sigma_s}) +\frac{3}{4} \sqrt{(\frac{\sigma_z}{\sigma_s})^2+4(\frac{\sigma_{\theta z}}{\sigma_s})^2}=1\tag{80} 41(σsσz)+43(σsσz)2+4(σsσθz)2=1(80)
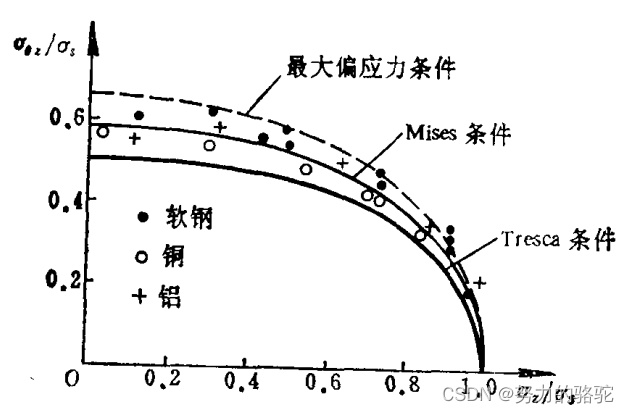
将实验结果画在一张图中,可见实验结果更接近Mises屈服条件,最大偏应力屈服条件其次。
这篇关于【小呆的力学笔记】弹塑性力学的初步认知五:初始屈服条件(3)的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!




