内积专题
【解析几何笔记】8.向量的投影与内积
8. 向量的投影与内积 复习前面的知识:,若BCE三点共线,则 A E ⃗ = ( 1 − s ) A B ⃗ + s A C ⃗ , ( B , C , E ) = μ ⇒ s = μ 1 + μ , 1 − s = 1 1 + μ \vec{AE}=(1-s)\vec{AB}+s\vec{AC},(B,C,E)=\mu\Rightarrow s=\frac{\mu}{1+\mu},1-s=
理解矩阵内积与矩阵乘法的区别及其应用
文章目录 矩阵内积(逐元素乘积)矩阵内积的用途矩阵乘法(矩阵积)矩阵乘法的用途区别总结结论 在数据科学、机器学习、计算机图形学和图像处理等领域,矩阵运算是非常基础且重要的操作。然而,矩阵内积和矩阵乘法这两种看似相似的操作却有着不同的计算方式和应用场景。本文将详细解释它们的区别及各自的用途。 矩阵内积(逐元素乘积) 矩阵内积,或逐元素乘积,是指两个相同尺寸的矩阵对应位置元
6. 神经网络的内积
目录 1. 准备知识 1.1 NumPy 的多维数组 1.2 矩阵乘法 1.2.1 矩阵乘法顺序 1.2.2 矩阵乘法范例 2. 神经网络的内积 2.1 使用场合 2.2 Python 实现 1. 准备知识 1.1 NumPy 的多维数组 大家应该对多维数组都很熟悉,我不再多言。在 NumPy 模块中,可以使用 np.ndim() ( Return
SIGIR2021 | 超越I2I和向量内积,淘宝新一代召回范式:PDN模型
摘要 一般来说业务的推荐系统的常用的召回算法有两个范式,相似度索引范式(如I2I),EBR范式(如DeepMatch)。I2I范式缺点在于对共现少的pair难以泛化,难以建模U2I部分,从而模型缺乏准确和个性化。EBR范式虽建模了U2I部分,将用户的兴趣整合成了一个向量。但却无法建模用户每一个行为和打分item之间的关系(类似于Target Attention),从而召回即缺乏多样性。为了融合
mini_batch 中在特征的层面拉近同类内积 推远异类内积
在mini batch中,我要返回一个(batch_size, dim)尺寸的张量,然后计算相同类别之间的平均内积,和异类之间的平均内积。 这里其实有一点可以考虑,咱们到底是将内积作为目标函数来优化好,还是将距离作为目标函数来优化好呢? 如果是内积的话,同类的好说,同类之间的内积越接近1越好,异类之间的内积,是接近0好,还是-1好呢?这确实是一个问题。 在我下面的代码中,我是将异类的内积设
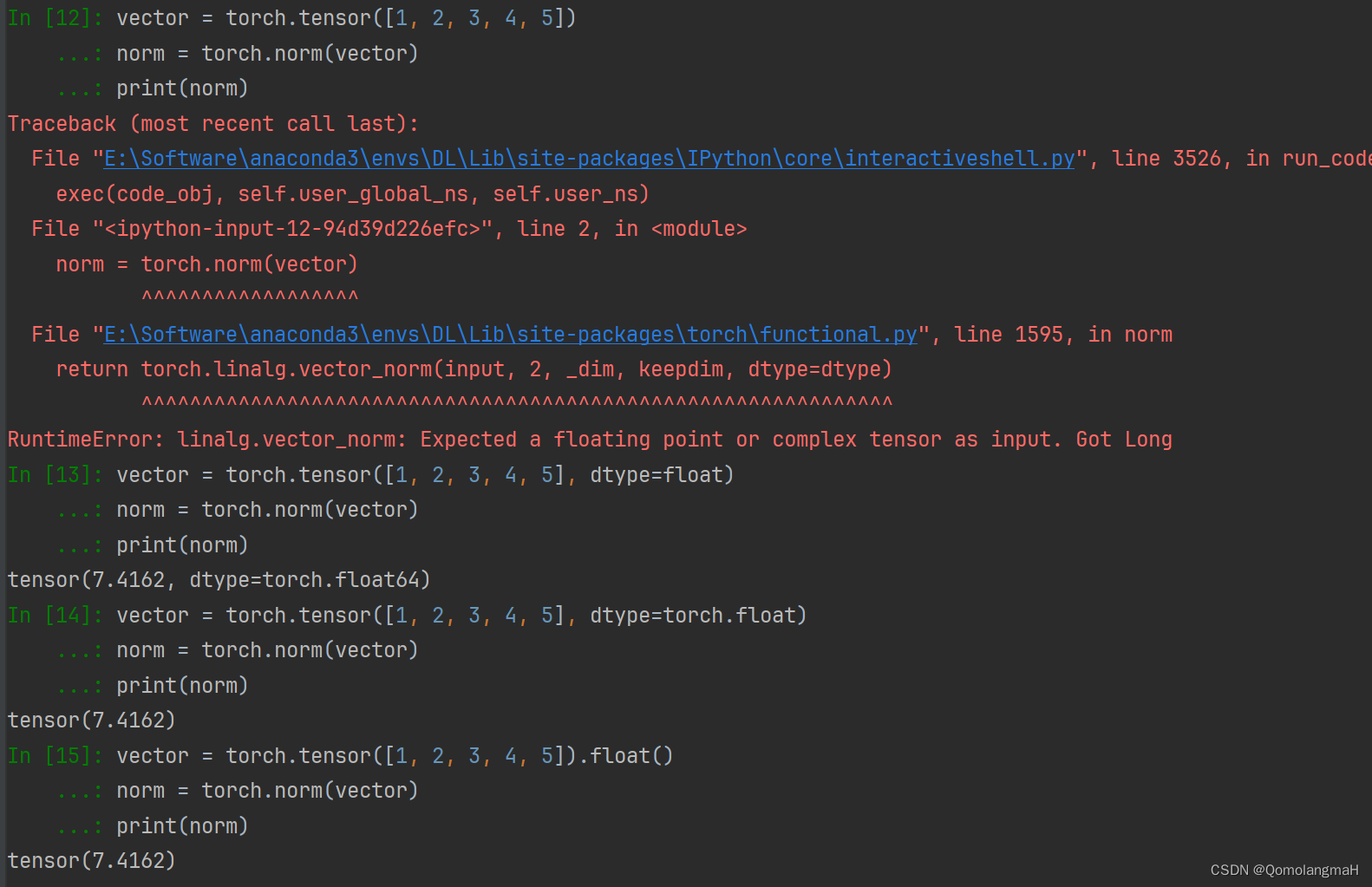
【深度学习】Pytorch 系列教程(三):PyTorch数据结构:2、张量的数学运算(1):向量运算(加减乘除、数乘、内积、外积、范数、广播机制)
文章目录 一、前言二、实验环境三、PyTorch数据结构0、分类1、Tensor(张量)1. 维度(Dimensions)2. 数据类型(Data Types)3. GPU加速(GPU Acceleration) 2、张量的数学运算1. 向量运算a. 简单运算b. 广播操作c. 运算函数加法add乘法mul内积(点积)dot外积(叉积)cross范数norm 一、前言
为什么两个向量的内积等于模长乘夹角?
为什么两个向量的内积等于模长乘夹角? 已知两个向量 a = [ a 1 , a 2 ] a=[a_1,a_2] a=[a1,a2]和 b = [ b 1 , b 2 ] b=[b_1,b_2] b=[b1,b2],他们的内积为 a b = a 1 b 1 + a 2 b 2 ab=a_1b_1+a_2b_2 ab=a1b1+a2b2,看书上的定义该内积的值是一个
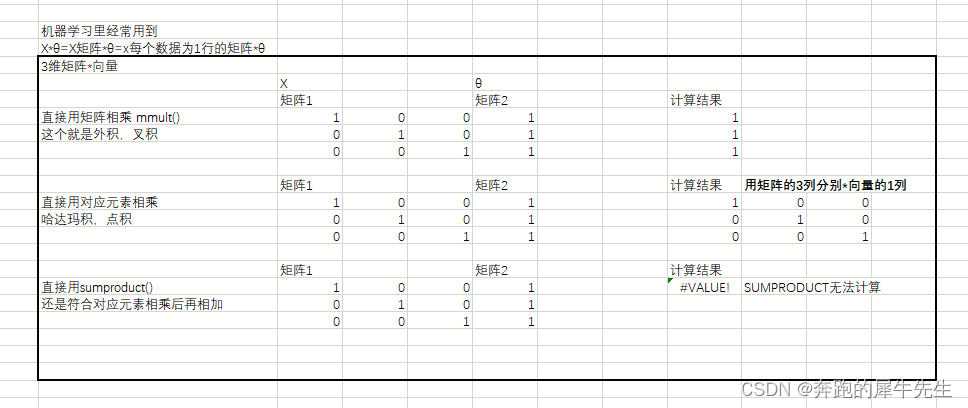
线性代数的学习和整理23:用EXCEL和python 计算向量/矩阵的:内积/点积,外积/叉积
目录 1 乘法 1.1 标量乘法(中小学乘法) 1.1.1 乘法的定义 1.1.2 乘法符合的规律 1.2 向量乘法 1.2.1 向量:有方向和大小的对象 1.2.2 向量的标量乘法 1.2.3 常见的向量乘法及结果 1.2.4 向量的其他乘法及结果 1.2.5 向量的模长(长度) 模长的计算公式 1.2.6 距离 2 向量的各种乘法 2.1 向量的标量乘法(
线性代数的学习和整理23:用EXCEL计算 向量/向量组的点乘 (内积) (建设ing)
目录 前言:EXCEL里的的向量相关计算公式 0.1 EXCEL里相关公式 0.2 先说结论:向量组的点乘公式和 向量组的点乘公式不一样 1 向量的点乘 (内积) 1.1 向量的点乘公式 1.2 EXCEL里向量点乘的计算 编辑 1.3 向量点乘的性质 1.3.1 内积的公式A*B=|A|*|B|*cos(θ) 1.3.1.2 cos曲线
69、python - 利用向量内积来优化卷积运算
上一节介绍了利用 python 实现的原始卷积版本性能很差的原因,不知道各位同学有尝试的么? 这一节介绍下如何对卷积的乘累加进行一次优化:我们利用 np.dot 来进行优化。 np.dot np.dot 是 numpy 库提供的一个函数,用来计算两个向量的点积,或者叫内积。那什么是内积呢? 假设有两个向量: import numpy as npa = np.array([1, 2, 3
向量的内积(点乘)与外积(叉乘)
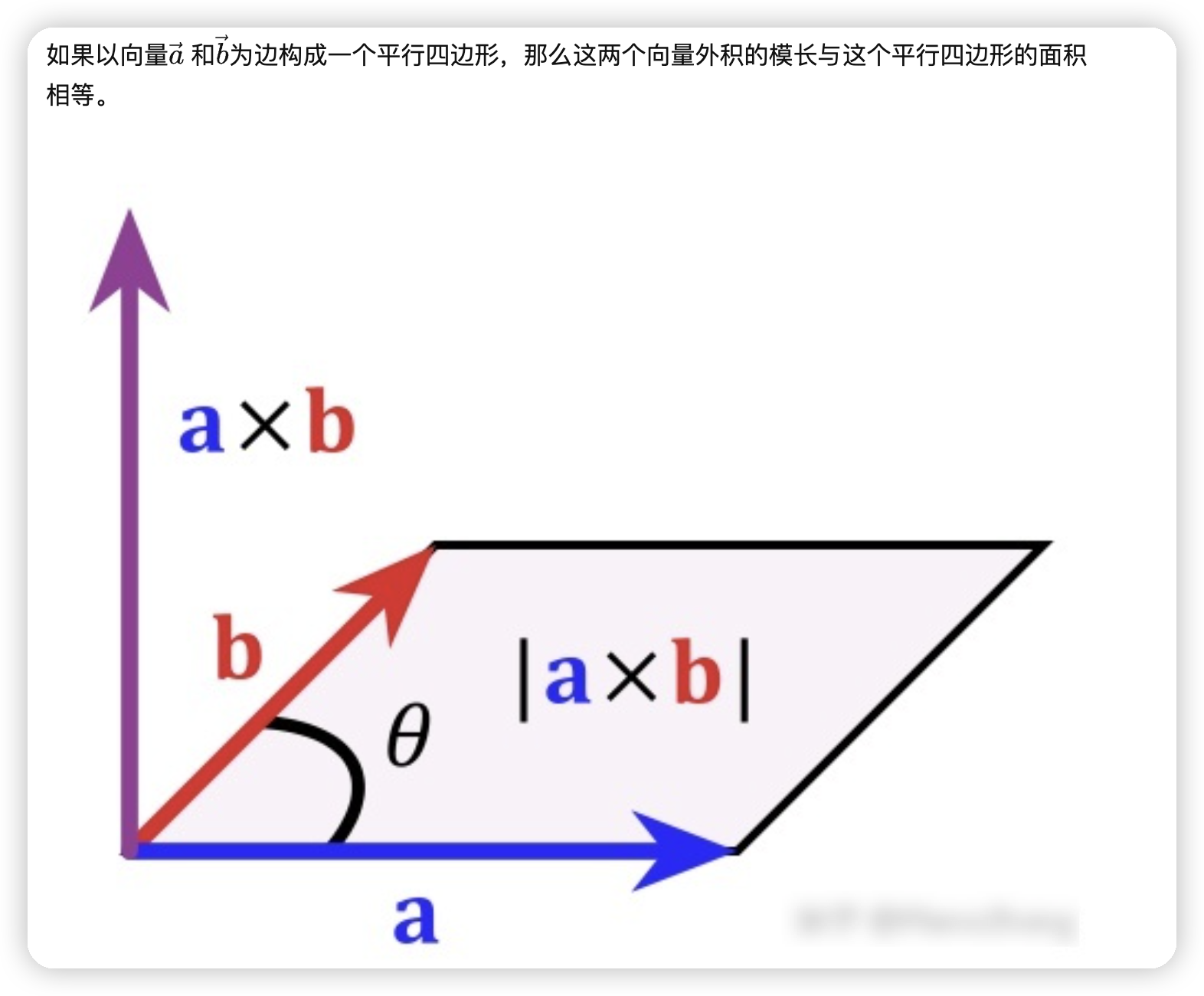
向量的内积(点乘)与外积(叉乘) 向量的内积=点乘 向量的外积=叉乘 向量的内积(点乘) 内积的几何意义: 用来表征或计算两个向量之间的夹角在b向量在a向量方向上的投影。 向量的外积(叉乘) 两个向量的外积,又叫向量积、叉乘等。外积的运算结果是一个向量。并且两个向量的叉积与这两个向量组成的坐标平面垂直(右手定理) 叉乘的几何意义: 向量a和向量b的叉乘结果是一个向量
线性代数(五)向量空间——向量空间的基 维数 内积 基的规范正交化
本节主要知识点 1.向量空间的定义:对加法和乘法运算封闭的非空的n维向量的集合 2.向量空间的基:向量空间中一组线性无关的向量,并且其他向量可以用这组向量线性表示。一组基中含有的向量个数为向量空间的维数。向量空间的基不是唯一的,但维数是确定的。 3.内积:对应坐标相乘后累加即可。 4.范数:向量的模长,及向量本身做内积后的算术平方根的值。 5.基的正交规范化:向量空间的一组基,两两正交而
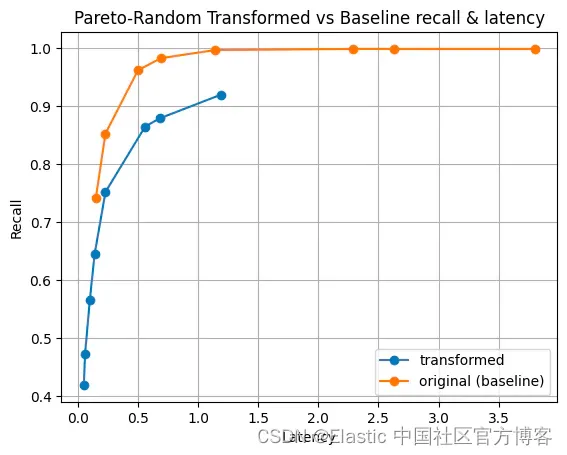
Elasticsearch:将最大内积引入 Lucene
作者:Benjamin Trent 目前,Lucene 限制 dot_product (点积) 只能在标准化向量上使用。 归一化迫使所有向量幅度等于一。 虽然在许多情况下这是可以接受的,但它可能会导致某些数据集的相关性问题。 一个典型的例子是 Cohere 构建的嵌入(embeddings)。 它们的向量使用幅度来提供更多相关信息。 那么,为什么不允许点积中存在非归一化向量,从而实现最大内
AM@向量代数@数量积@内积
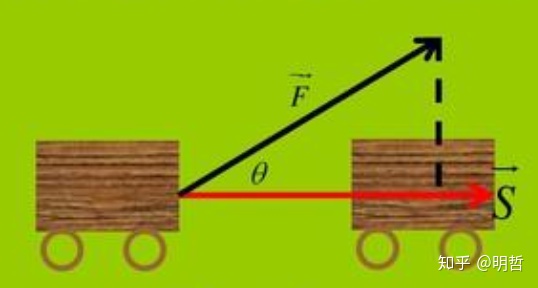
文章目录 abstract数学概念和运算的定义数量积(内积@点积)代数表示从ji'he 几何表示余弦定理和向量数量积 向量点积运算律交换律分配律👺结合律 数量积和恒力做功模型利用内积判断向量间的关系小结 abstract 两个向量间的乘法: 数量积向量积 两种向量的乘法都有对应的物理问题,相关的计算规则抽象自物理模型 数量积与恒力做功向量积与力矩 将物理问题模型抽象成数量
【数学】 4、向量的内积、外积、模长
文章目录 一、向量点乘(内积)1.1 几何意义1.2 点乘的代数定义,推导几何定义(用于求向量夹角)1.2.1 余弦定理 1.3 程序计算 二、向量叉乘(外积)2.1 几何意义 三、通俗理解内积和外积四、向量的模长 向量点乘、叉乘的概念和意义 一、向量点乘(内积) 点乘(Dot Product)的结果是点积,又称数量积或标量积(Scalar Product)。 1.1
Pytorch 基于im2col手动实现卷积conv2d(基于nn.Unfold实现卷积)(向量内积实现)
如果老老实实地实现卷积运算,估计要重复好几层的for语句。这样的实现有点麻烦,而且, NumPy中存在使用for语句后处理变慢的缺点(NumPy中,访问元素时最好不要用 for语句) 如上图所示,我们每次取的input,我们可以把它拉直,拉成一个行向量。它跟kernel进行元素相乘再求和,就相当于这个输入行向量,再跟kernel的列向量(将kernel拉成列向量)进行