相关文章
python 库 Numpy 中如何求取向量范数 np.linalg.norm(求范数)(向量的第二范数为传统意义上的向量长度),(如何求取向量的单位向量)
转载自: https://www.cnblogs.com/devilmaycry812839668/p/9352814.html 求取向量二范数,并求取单位向量(行向量计算) import numpy as npx=np.array([[0, 3, 4], [2, 6, 4]])y=np.linalg.norm(x, axis=1, keepdims=True)z=x/y x 为需
【解析几何笔记】8.向量的投影与内积
8. 向量的投影与内积 复习前面的知识:,若BCE三点共线,则 A E ⃗ = ( 1 − s ) A B ⃗ + s A C ⃗ , ( B , C , E ) = μ ⇒ s = μ 1 + μ , 1 − s = 1 1 + μ \vec{AE}=(1-s)\vec{AB}+s\vec{AC},(B,C,E)=\mu\Rightarrow s=\frac{\mu}{1+\mu},1-s=
【转】常见向量范数和矩阵范数
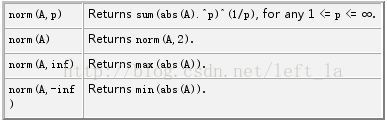
1、向量范数 1-范数:,即向量元素绝对值之和,matlab调用函数norm(x, 1) 。 2-范数:,Euclid范数(欧几里得范数,常用计算向量长度),即向量元素绝对值的平方和再开方,matlab调用函数norm(x, 2)。 ∞-范数:,即所有向量元素绝对值中的最大值,matlab调用函数norm(x, inf)。 -∞-范数:,即所有向量元素绝对值中的最小值,matlab调用函数nor
线性方程求解之 二范数类型
求解线性系统 在线性代数中我们经常需要求解具有m个方程 ,n 个 未知量的问题。这个问题可以以简洁的形式 表示为 Ax=b Ax=b 其中 A A 是一个m×nm\times n , x x是一个长度为n的向量(如不特别强调,都是列向量) ,bb是一个长度为m 的向量。如果 m=n m = n ,并且 满秩(各行向量或列向量线性无关) ,则这个线性方程的解为 x=A−1b x=A^{
线性代数|机器学习-P9向量和矩阵范数
文章目录 1. 向量范数2. 对称矩阵S的v范数3. 最小二乘法4. 矩阵范数 1. 向量范数 范数存在的意义是为了实现比较距离,比如,在一维实数集合中,我们随便取两个点4和9,我们知道9比4大,但是到了二维实数空间中,取两点A(1,0),B(3,4),这时候我们就没办法比较它们之间的大小了,因为它们不是可以比较的实数,于是我们引入了范数这个概念,把我们的A,B两个点变成 ∣ ∣
矩阵1-范数与二重求和的求和可交换
矩阵1-范数与二重求和的求和可交换 1、矩阵1-范数 A = [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] A = \begin{bmatrix} a_{11} &a_{12} &\cdots &a_{1n} \\ a_{21} &a_{22} &\cdots &a_{2n} \\ \vdots &\v
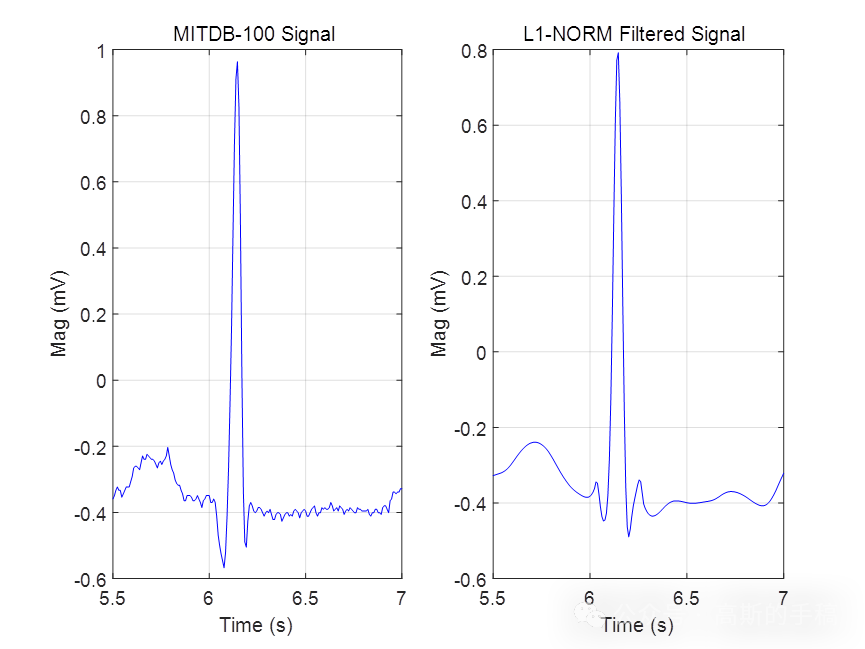
基于L1范数惩罚的稀疏正则化最小二乘心电信号降噪方法(Matlab R2021B)
L1范数正则化方法与Tikhonov正则化方法的最大差异在于采用L1范数正则化通常会得到一个稀疏向量,它的非零系数相对较少,而Tikhonov正则化方法的解通常具有所有的非零系数。即:L2范数正则化方法的解通常是非稀疏的,并且解的结果在一定范围内是发散的,而L1范数正则化方法的解通常是稀疏的。 鉴于此,采用L1范数惩罚的稀疏正则化最小二乘方法对心电信号进行降噪,算法可迁移至金融时间序列,地震信号
理解矩阵内积与矩阵乘法的区别及其应用
文章目录 矩阵内积(逐元素乘积)矩阵内积的用途矩阵乘法(矩阵积)矩阵乘法的用途区别总结结论 在数据科学、机器学习、计算机图形学和图像处理等领域,矩阵运算是非常基础且重要的操作。然而,矩阵内积和矩阵乘法这两种看似相似的操作却有着不同的计算方式和应用场景。本文将详细解释它们的区别及各自的用途。 矩阵内积(逐元素乘积) 矩阵内积,或逐元素乘积,是指两个相同尺寸的矩阵对应位置元