本文主要是介绍Elasticsearch:将最大内积引入 Lucene,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
作者:Benjamin Trent

目前,Lucene 限制 dot_product (点积) 只能在标准化向量上使用。 归一化迫使所有向量幅度等于一。 虽然在许多情况下这是可以接受的,但它可能会导致某些数据集的相关性问题。 一个典型的例子是 Cohere 构建的嵌入(embeddings)。 它们的向量使用幅度来提供更多相关信息。
那么,为什么不允许点积中存在非归一化向量,从而实现最大内积呢? 有什么大不了的?
负值和 Lucene 优化
Lucene要求分数非负,因此在析取 (disjunctive query) 查询中多匹配一个子句只能使分数更高,而不是更低。 这实际上对于动态修剪优化(例如 block-max WAND)非常重要,如果某些子句可能产生负分数,则其效率会大大降低。 此要求如何影响非标准化向量?
在归一化情况下,所有向量都在单位球面上。 这允许通过简单的缩放来处理负分数。
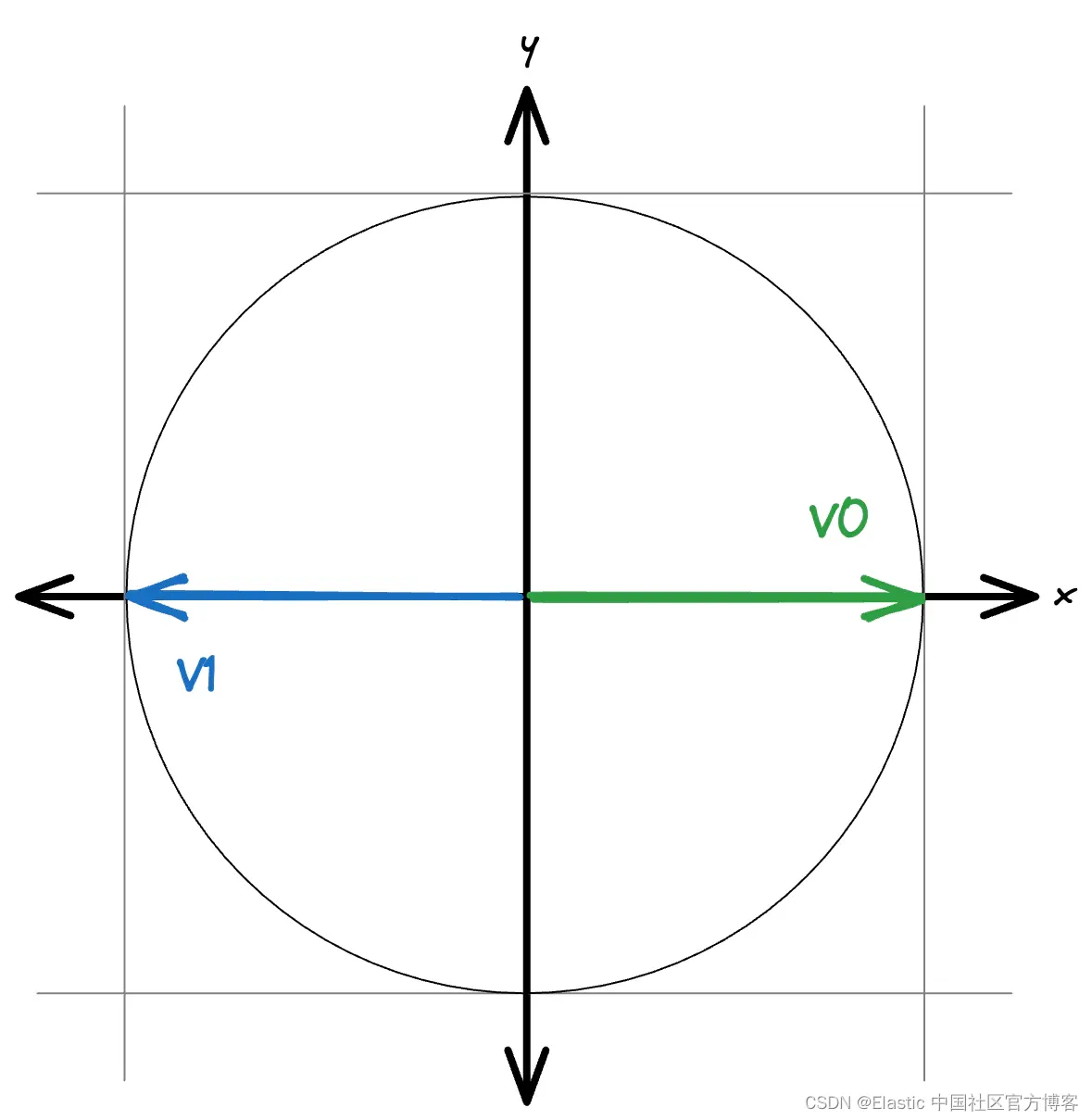
当向量保持其大小时,可能值的范围是未知的。
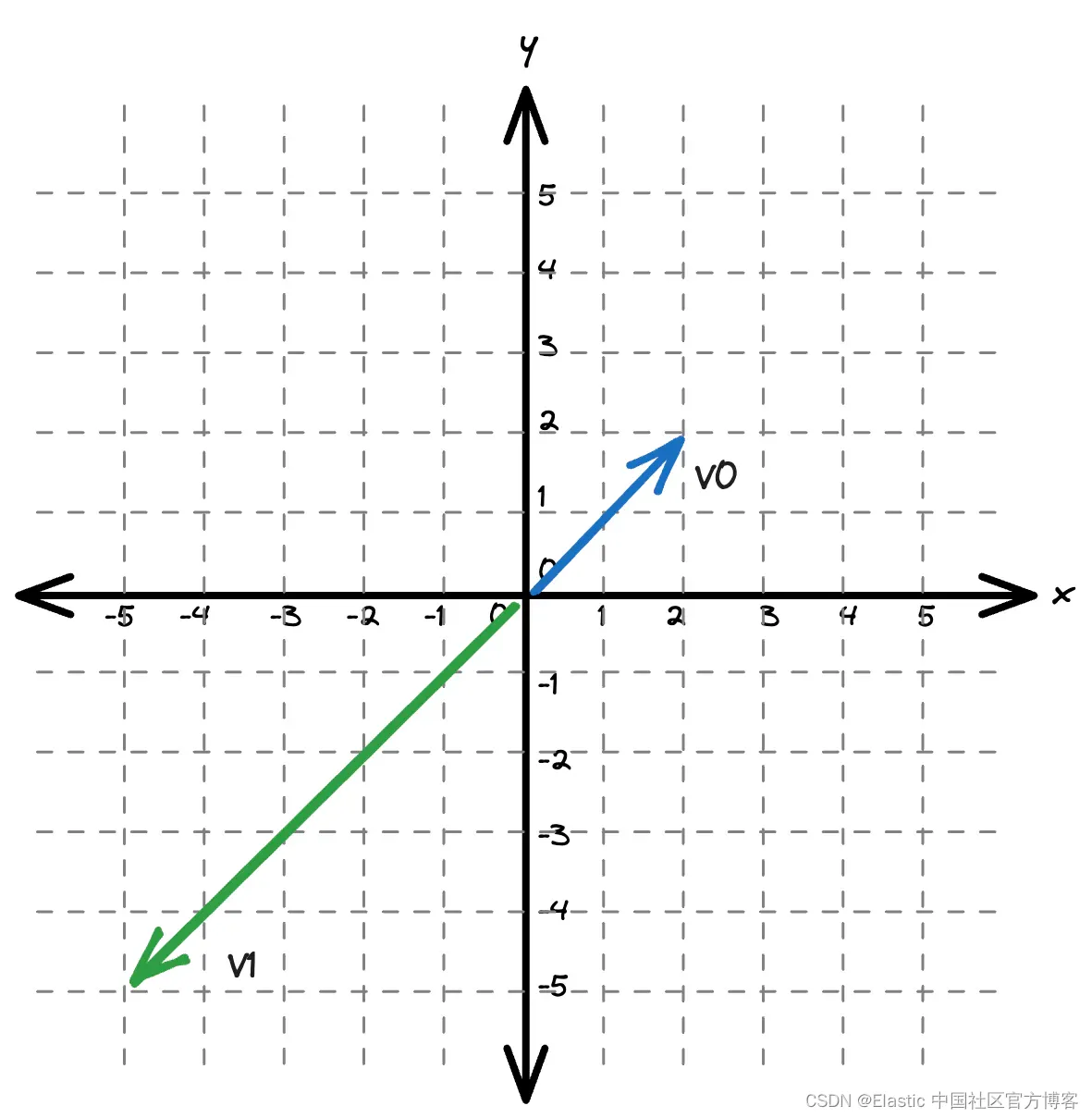
为了允许 Lucene 将 blockMax WAND 与非标准化向量结合使用,我们必须缩放分数。 这是一个相当简单的解决方案。 Lucene 将使用简单的分段函数缩放非标准化向量:
if (dotProduct < 0) {return 1 / (1 + -1 * dotProduct);
}
return dotProduct + 1;现在,所有负分数都在 0 -1 之间,所有正分数都在 1 以上。这仍然可以确保较高的值意味着更好的匹配并消除负分数。 很简单,但这不是最后的障碍。
三角形问题
最大内积不遵循与简单欧几里得空间相同的规则。 三角不等式的简单假设知识被抛弃。 不直观的是,向量不再最接近其自身。 这可能会令人不安。 Lucene 的向量底层索引结构是分层可导航小世界 (HNSW)。 这是基于图的算法,它可能依赖于欧几里得空间假设。 或者在非欧几里得空间中探索图会太慢吗?
一些研究表明,快速搜索需要转换到欧几里得空间。 其他人则经历了更新向量存储以强制转换为欧几里得空间的麻烦。
这导致我们停下来深入挖掘一些数据。 关键问题是:HNSW 是否通过最大内积搜索提供良好的召回率和延迟? 虽然 HNSW 最初的论文和其他已发表的研究表明确实如此,但我们需要进行尽职调查。
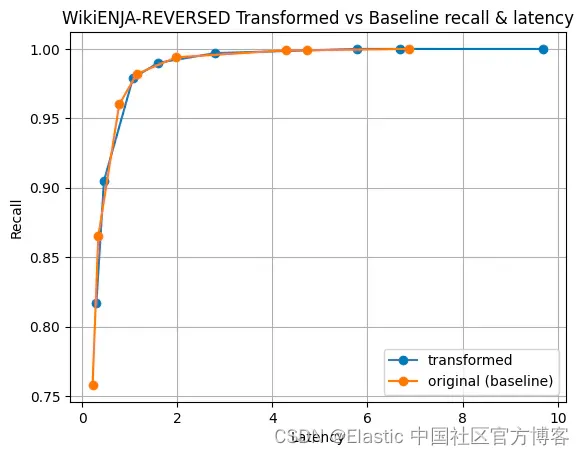
我们进行的实验很简单。 所有的实验都是在真实数据集或稍微修改的真实数据集上进行的。 这对于基准测试至关重要,因为现代神经网络创建符合特定特征的向量(请参阅本文第 7.8 节中的讨论)。 我们测量了非标准化向量的延迟(以毫秒为单位)与召回率。 将数字与具有相同测量值但采用欧几里德空间变换的数字进行比较。 在每种情况下,向量都被索引到 Lucene 的 HNSW 实现中,并且我们测量了 1000 次查询迭代。 每个数据集考虑了三种单独的情况:按大小顺序插入的数据(从小到大)、按随机顺序插入的数据以及按相反顺序插入的数据(从大到小)。
以下是 Cohere 真实数据集的一些结果:
 |  |
|
|
 |  |
 |
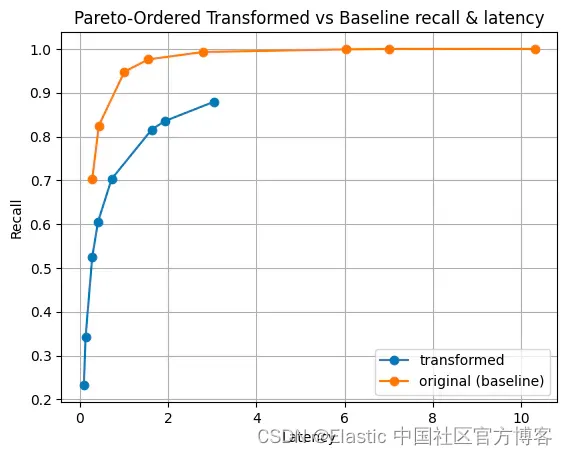
我们还针对一些合成数据集进行了测试,以确保我们的严谨性。 我们使用 e5-small-v2 创建了一个数据集,并通过不同的统计分布缩放了向量的大小。 为了简洁起见,我将仅显示两个分布。
 |  |
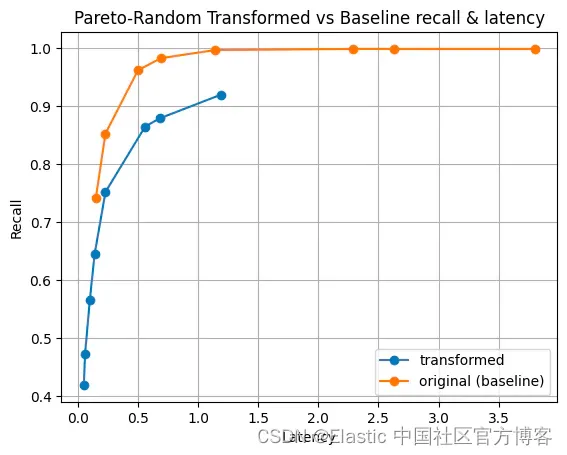 |
图 6:幅度的伽马分布。 这种分布可能具有很高的方差,并使其在我们的实验中独一无二。
在我们所有的实验中,唯一需要进行转换的是使用伽玛分布创建的合成数据集。 即使这样,向量也必须以相反的顺序插入,首先是最大幅度,以证明变换的合理性。 这些都是例外情况。
如果你想了解所有实验以及整个过程中的所有错误和改进,请参阅 Lucene Github 问题,其中包含所有详细信息(以及过程中的错误)。 这是一个开放式研究和开发的项目!
结论
这是一个相当长的旅程,需要进行多次调查才能确保 Lucene 能够支持最大内积。 我们相信数据不言自明。 无需进行重大转换或对 Lucene 进行重大更改。 所有这些工作将很快解锁 Elasticsearch 的最大内积支持,并允许 Cohere 提供的模型成为 Elastic Stack 中的一等公民。
注:最大内积已经在 8.11 中进行了支持!
原文:Bringing Maximum-Inner-Product into Lucene — Elastic Search Labs
这篇关于Elasticsearch:将最大内积引入 Lucene的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!






