伯努利专题
伯努利朴素贝叶斯解析:面向初学者的带代码示例的视觉指南
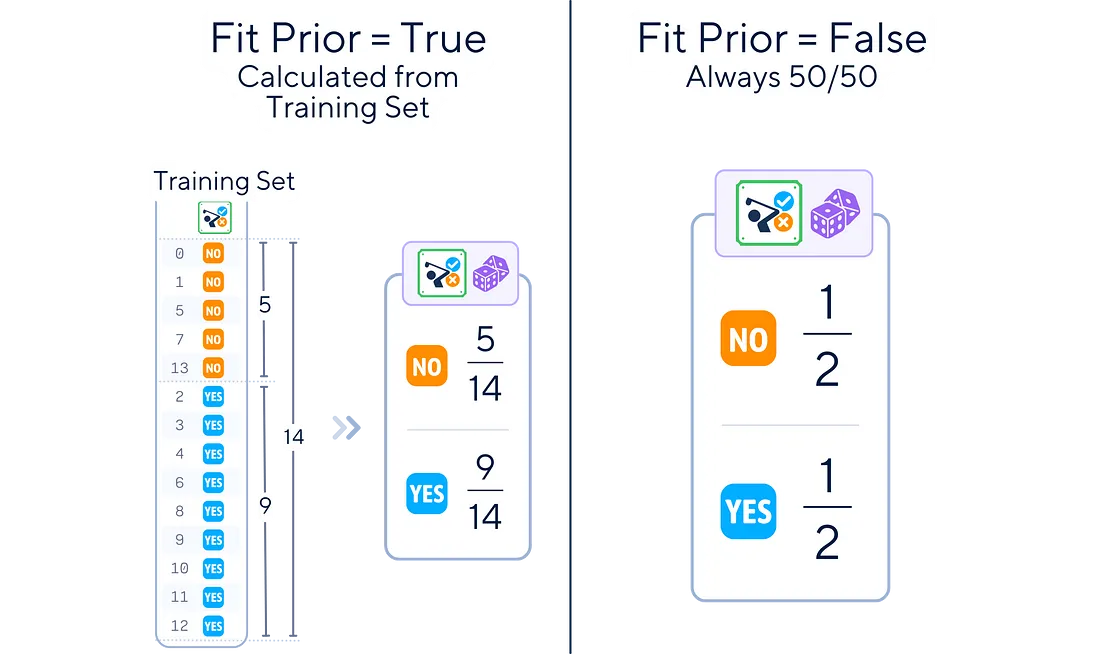
通过二进制简单性释放预测能力,欢迎来到雲闪世界。 添加图片注释,不超过 140 字(可选) 与虚拟分类器的基线方法或基于相似性的 KNN 推理不同,朴素贝叶斯利用了概率论。它结合了每个“线索”(或特征)的个体概率来做出最终预测。这种简单而强大的方法已被证明在各种机器学习应用中具有无价的价值。 定义 朴素贝叶斯是一种使用概率对数据进行分类的机器学习算法。它基于贝叶斯定理,即计算条件概率的公式
AI学习指南机器学习篇-伯努利朴素贝叶斯算法简介
AI学习指南机器学习篇-伯努利朴素贝叶斯算法简介 1. 伯努利朴素贝叶斯算法的原理 1.1 算法的基本思想 伯努利朴素贝叶斯算法是基于贝叶斯定理和特征条件独立假设的分类算法。其基本思想是通过先验概率和类条件概率来计算后验概率,从而实现对样本进行分类。 1.2 分类问题中的应用 伯努利朴素贝叶斯算法在文本分类、垃圾邮件过滤、情感分析等领域有着广泛的应用。在文本分类中,可以通过统计文档中单词
思考伯努利试验的两种组合思想
思考伯努利试验的两种组合思想 @(概率论) 伯努利试验(Bernoulli experiment)的定义 先从最基本的定义开始思考: 伯努利试验(Bernoulli experiment):是在同样的条件下重复地、相互独立地进行的一种随机试验。其特点是该随机试验只有两种可能结果:发生或者不发生。然后我们假设该项试验独立重复地进行了n次,那么我们就称这一系列重复独立的随机试验为n重伯努利试验
伯努利试验和二项分布
伯努利试验和二项分布 概念 设试验E只有两个可能结果,A和非A,则称E为伯努利试验,设P(A)=p(0 < p < 1),此时P(非A)=1-p;将E独立重复地进行n次,则称这一串重复的独立试验为n重伯努利试验。 二项分布 在数学中,典型的伯努利试验有,将硬币抛n次,就是n重伯努利试验,抛一个骰子,若A表示得到“1”点,q表示非“A”点,将骰子抛n次,就是n重伯努利试验。 以X表示n重伯
【概率论】5-2:伯努利和二项分布(The Bernoulli and Binomial Distributions)
原文地址1:https://www.face2ai.com/Math-Probability-5-2-the-Bernoulli-and-Binomial-Distributions转载请标明出处 Abstract: 本文介绍Bernoulli Distribution (伯努利分布)和Binomial Distribution(二项分布) Keywords: Bernoulli Distrib
51nod 1228 序列求和【伯努利数】【自然数幂的和】
文章目录 题目链接:伯努利数来求递推式来求 题目链接: http://www.51nod.com/onlineJudge/questionCode.html#!problemId=1228&judgeId=550328 就是求自然数幂的和 伯努利数来求 早就听说过伯努利数了,但是感觉太难了,一直没管,但是今天因为队友的一道题,突然推出一个递推式,貌似阔以用 O ( n 2 )
CNN中的伯努利分布与二项式分布
伯努利分布是什么? 伯努利分布是二项分布的一种特殊情况。在伯努利试验中,只有两个可能的结果,通常用1和0表示,例如成功和失败、正面和反面等。伯努利分布描述了在单次伯努利试验中发生成功的概率。它的概率质量函数为: P(X=k) = p^k * (1-p)^(1-k) 其中,p为成功的概率,k为观察到的结果(成功为1,失败为0)。 伯努利分布的期望值为p,方差为p(1-p)。它适用于一些简单的二
朴素贝叶斯算法系列:多项式贝叶斯、高斯贝叶斯、伯努利贝叶斯
导入库 from sklearn.naive_bayes import MultinomialNB, GaussianNB, BernoulliNB 多项式贝叶斯 def MultinomialNB_Classifier(self, fea_train, trainLabel,testPadSqe):"""模型算法:多项式贝叶斯算法"""clf = Multin
伯努利分布期望,方差推导
伯努利分布的期望,方差推导比较简单 首先要知道伯努利分布的概率质量函数: p(x)={p,1−p,if x=1if x=0 p(x)= \begin{cases} p, & \text {if $x=1$} \\ 1-p, & \text{if $x=0$} \end{cases}期望推导:
伯努利二项分布的相对高概率与实际的低概率
伯努利二项分布的相对高概率与实际的低概率 计算公式 P ( X = k ) = C n k p k ( 1 − p ) n − k P(X=k)=C_{n}^{k} p^k(1-p)^{n-k} P(X=k)=Cnkpk(1−p)n−k n n n 表示试验次数, p p p 表示事件出现的概率, k k k 表示事件出现的次数 简单理解就是,盒子里有total个小球,有 p ∗ t