伯努利朴素贝叶斯解析：面向初学者的带代码示例的视觉指南

通过二进制简单性释放预测能力，欢迎来到雲闪世界。

添加图片注释，不超过 140 字（可选）

与虚拟分类器的基线方法或基于相似性的 KNN 推理不同，朴素贝叶斯利用了概率论。它结合了每个“线索”（或特征）的个体概率来做出最终预测。这种简单而强大的方法已被证明在各种机器学习应用中具有无价的价值。 定义 朴素贝叶斯是一种使用概率对数据进行分类的机器学习算法。它基于贝叶斯定理，即计算条件概率的公式。“朴素”部分指的是它的关键假设：它将所有特征视为彼此独立，即使它们在现实中可能并非如此。这种简化虽然通常不切实际，但大大降低了计算复杂性，并且在许多实际场景中效果很好。

添加图片注释，不超过 140 字（可选）

朴素贝叶斯分类器的主要类型 朴素贝叶斯分类器主要有三种类型。这些类型之间的关键区别在于它们对特征分布的假设：

1. 伯努利朴素贝叶斯：适用于二进制/布尔特征。它假设每个特征都是一个二进制值（0/1）变量。

2. 多项式朴素贝叶斯：通常用于离散计数。它经常用于文本分类，其中特征可能是字数。

3. 高斯朴素贝叶斯：假设连续特征遵循正态分布。

添加图片注释，不超过 140 字（可选）

首先，我们先来关注最简单的伯努利 NB。其名称中的“伯努利”源于每个特征都是二值化的假设。 使用的数据集 在本文中，我们将使用这个人工高尔夫数据集（灵感来自 [1]）作为示例。该数据集根据天气状况预测一个人是否会打高尔夫球。

添加图片注释，不超过 140 字（可选）

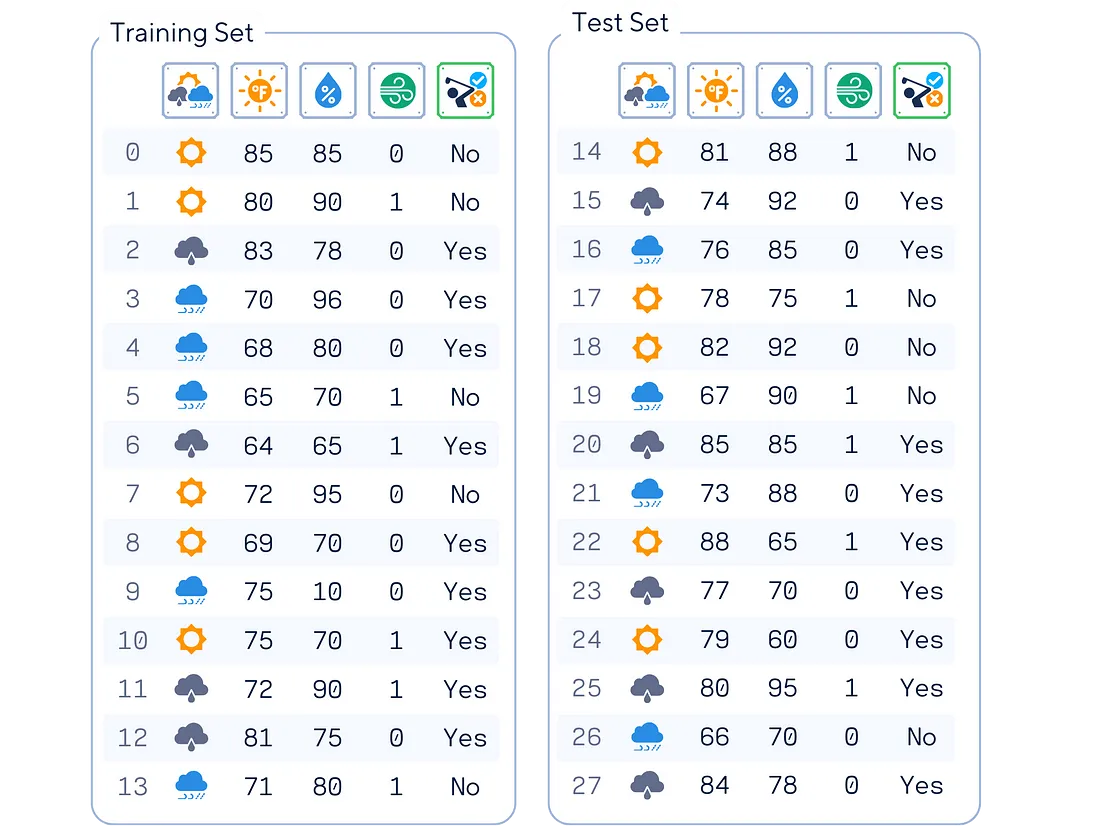
# 导入数据集 # 从sklearn.model_selection导入train_test_split 从sklearn.metrics导入accuracy_score 导入pandas作为pd 导入numpy作为np dataset_dict = { 'Outlook'：[ 'sunny'，'sunny'，'overcast'，'rain'，'rain'，'rain'，' overcast'，'sunny '，'rain'，'sunny'，' rain'，'sunny'，'overcast' ， ' rain'，' sunny ' ， 'overcast' ，'rain'，' sunny' ，'overcast'，'rain'，'sunny' ， ' rain' ，'sunny'，'overcast'，'rain'，'阴天' ], '温度' : [ 85.0 , 80.0 , 83.0 , 70.0 , 68.0 , 65.0 , 64.0 , 72.0 , 69.0 , 75.0 , 75.0 , 72.0 , 81.0 , 71.0 , 81.0 , 74.0 , 76.0 , 78.0 , 82.0 , 67.0 , 85.0 , 73.0 , 88.0 , 77.0 , 79.0 , 80.0 , 66.0 , 84.0 ], '湿度' : [ 85.0 , 90.0 , 78.0 , 96.0、80.0、70.0、65.0、95.0、70.0、80.0、70.0、90.0、75.0、80.0、​​​​​​​​​​​​​88.0、92.0、85.0、75.0、​​​​​​ 92.0 , 90.0 , 85.0 , 88.0 , 65.0 , 70.0 , 60.0 , 95.0 , 70.0 , 78.0 ] ，' 风' ：[假，真，假...​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​​ , '是' , '是' , '是' , '否' , '否' , '是' , '是' , '否' , '否' , '是' , '是' , '是' , '是' , '是' , '是' , '是' , '否' , '是' ] } df = pd.DataFrame(dataset_dict) # 对 'Outlook' 列进行 ONE-HOT 编码df = pd.get_dummies(df, columns=[ 'Outlook' ], prefix= '' , prefix_sep= '' , dtype= int ) # 将 'Windy' (bool) 和 'Play' (binary) 列转换为二进制指标df[ 'Wind' ] = df[ '风' ]。astype( int ) df[ 'Play' ] = (df[ 'Play' ] == 'Yes' ).astype( int ) # 设置特征矩阵X和目标向量y X, y = df.drop(columns= 'Play' ), df[ 'Play' ] # 将数据分成训练集和测试集 X_train, X_test, y_train, y_test = train_test_split(X, y, train_size= 0.5 , shuffle= False ) print (pd.concat([X_train, y_train], axis= 1 ), end= '\n\n' ) print (pd.concat([X_test, y_test], axis= 1 )) 我们将通过将特征转换为二进制来针对伯努利朴素贝叶斯进行稍微调整。

添加图片注释，不超过 140 字（可选）

# 对分类后的列进行独热编码，然后删除它们，但对训练集和测试集分别执行此操作 # 为训练集定义“温度”和“湿度”类别 X_train[ '温度' ] = pd.cut(X_train[ '温度' ], bins=[ 0 , 80 , 100 ], labels=[ '温暖' , '热' ]) X_train[ '湿度' ] = pd.cut(X_train[ '湿度' ], bins=[ 0 , 75 , 100 ], labels=[ '干燥' , '湿度' ]) # 类似地，为测试集定义 X_test[ '温度' ] = pd.cut(X_test[ '温度' ], bins=[ 0 , 80 , 100 ], labels=[ 'Warm' , 'Hot' ]) X_test[ 'Humidity' ] = pd.cut(X_test[ 'Humidity' ], bins=[ 0 , 75 , 100 ], labels=[ 'Dry' , 'Humid' ]) # 对分类列进行独热编码 one_hot_columns_train = pd.get_dummies(X_train[[ 'Temperature' , 'Humidity' ]], drop_first= True , dtype= int ) one_hot_columns_test = pd.get_dummies(X_test[[ 'Temperature' , 'Humidity' ]], drop_first= True , dtype= int ) # 从训练和测试集中删除分类列 X_train = X_train.drop([ 'Temperature' , '湿度' ], axis= 1 ) X_test = X_test.drop([ '温度' , '湿度' ], axis= 1 ) # 将独热编码列与原始 DataFrames 连接 X_train = pd.concat([one_hot_columns_train, X_train], axis= 1 ) X_test = pd.concat([one_hot_columns_test, X_test], axis= 1 ) print (pd.concat([X_train, y_train], axis= 1 ), '\n' ) print (pd.concat([X_test, y_test], axis= 1 ))

主要机制 伯努利朴素贝叶斯对每个特征为 0 或 1 的数据进行操作。

1. 计算训练数据中每个类别的概率。

2. 对于每个特征和类别，计算给定类别时特征为 1 和 0 的概率。

3. 对于新实例：对于每个类，将其概率乘以该类每个特征值（0 或 1）的概率。

4. 预测结果概率最高的类别。

添加图片注释，不超过 140 字（可选）

训练步骤 伯努利朴素贝叶斯的训练过程涉及根据训练数据计算概率：

1. 类别概率计算：对于每个类别，计算其概率：（该类别中的实例数）/（实例总数）

添加图片注释，不超过 140 字（可选）

从分数导入分数 def calc_target_prob(attr):calc_target_prob (attr): total_counts = attr.value_counts (). sum () prob_series = attr.value_counts (). apply (lambda x: Fraction (x, total_counts) .limit_denominator ()) 返回 prob_series 打印( calc_target_prob (y_train))

2.特征概率计算：对于每个特征和每个类，计算：

• （此类中特征为 0 的实例数）/（此类中的实例数）

• （该类中特征为 1 的实例数）/（该类中的实例数）

添加图片注释，不超过 140 字（可选）

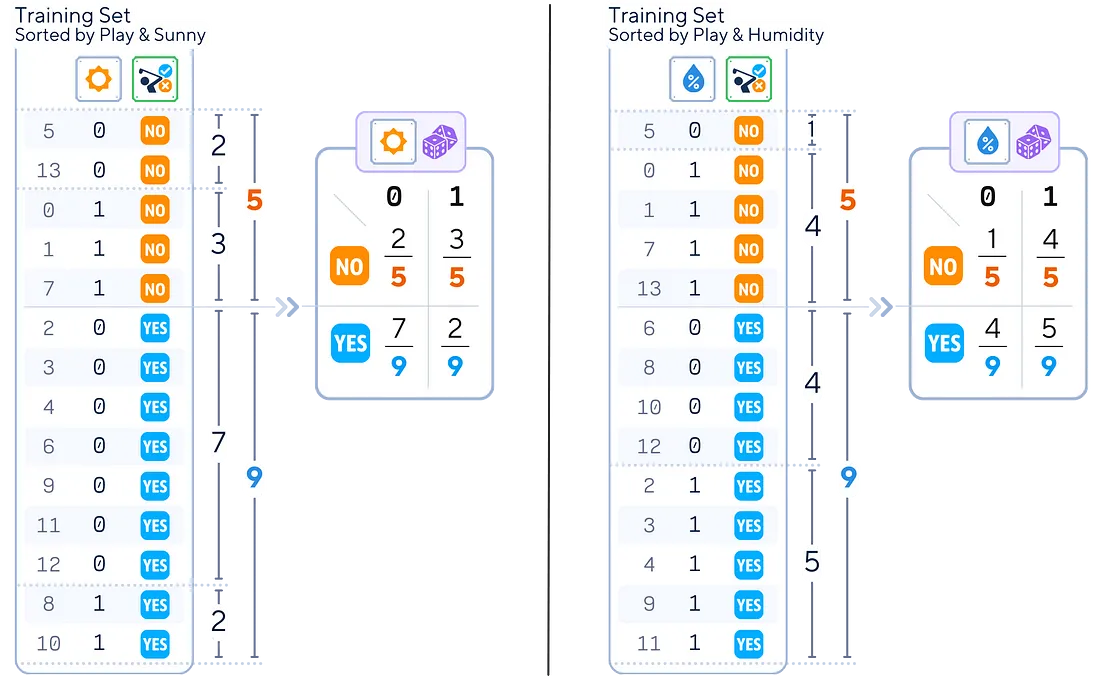
从分数导入分数 def sort_attr_label（attr，lbl）： 返回（pd.concat（[attr，lbl]，axis = 1） .sort_values（[attr.name，lbl.name]） .reset_index（） .rename（columns = { 'index'：'ID' }） .set_index（'ID'）） def calc_feature_prob（attr，lbl）： total_classes = lbl.value_counts（） counts = pd.crosstab（attr，lbl） prob_df = counts.apply（lambda x：[Fraction（c，total_classes[x.name]）。limit_denominator（）for c in x]） 返回prob_df 打印（sort_attr_label（y_train，X_train[ 'sunny' ]）） 打印（calc_feature_prob（X_train[ ‘阳光’ ], y_train))

添加图片注释，不超过 140 字（可选）

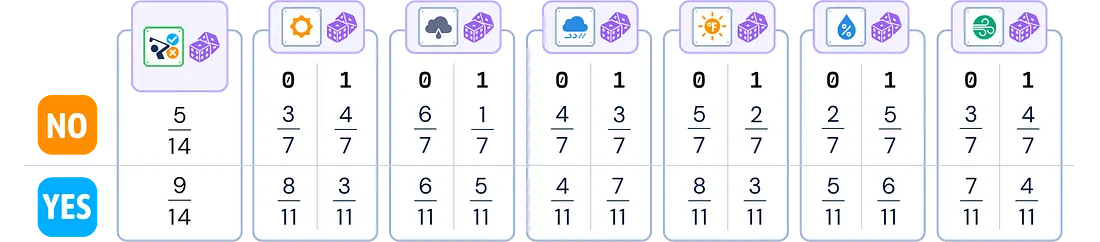
对于 X_train.columns 中的 col：.columns： 打印（calc_feature_prob（X_train[col]，y_train），“\n”）

3.平滑（可选）：在每个概率计算的分子和分母上添加一个小值（通常为 1），以避免零概率

添加图片注释，不超过 140 字（可选）

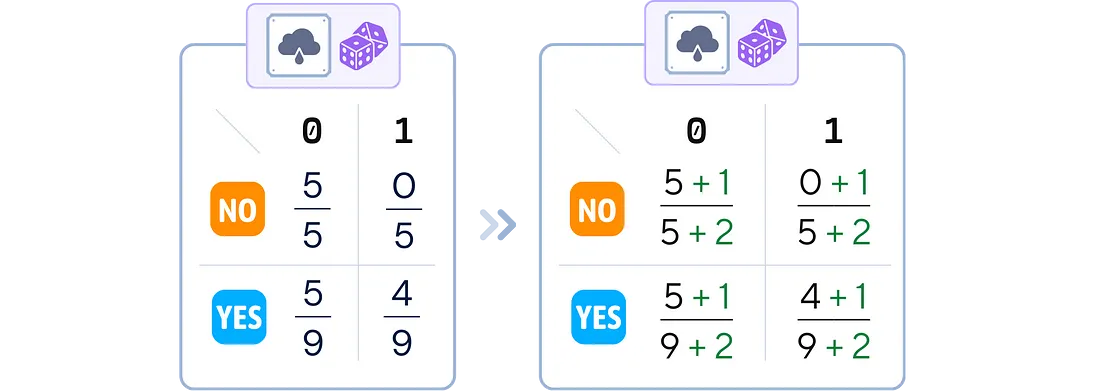
# 在 sklearn 中，上述所有过程都总结在这个 'fit' 方法中：总结如下‘fit’方法： from sklearn.naive_bayes import BernoulliNB nb_clf = BernoulliNB(alpha= 1 ) nb_clf.fit(X_train, y_train)

4.存储结果：保存所有计算出的概率以供分类时使用。

添加图片注释，不超过 140 字（可选）

分类步骤 给定一个特征为 0 或 1 的新实例：

1. 概率收集：对于每个可能的类别：

• 从该类发生的概率（类概率）开始。

• 对于新实例中的每个特征，收集该特征对于该类为 0/1 的概率。

添加图片注释，不超过 140 字（可选）

2.分数计算及预测：每个班级：

• 将所有收集到的概率相乘

• 结果为该课程的成绩

• 得分最高的类别是预测

添加图片注释，不超过 140 字（可选）

y_pred = nb_clf.预测（X_test） 打印（y_pred）

评估步骤

添加图片注释，不超过 140 字（可选）

# 评估分类器 print ( f"Accuracy: {accuracy_score(y_test, y_pred)} " )

关键参数 伯努利朴素贝叶斯有几个重要参数：

1. Alpha (α)：这是平滑参数。它为每个特征添加一个小计数以防止零概率。默认值通常为 1.0（拉普拉斯平滑），如前所示。

2. 二值化：如果您的特征尚未二值化，此阈值会对其进行转换。高于此阈值的任何值都变为 1，低于此阈值的任何值都变为 0。

对于 scikit-learn 中的 BernoulliNB，数值特征通常是标准化的，而不是手动二值化。然后模型内部将这些标准化值转换为二进制，通常使用 0（平均值）作为阈值。

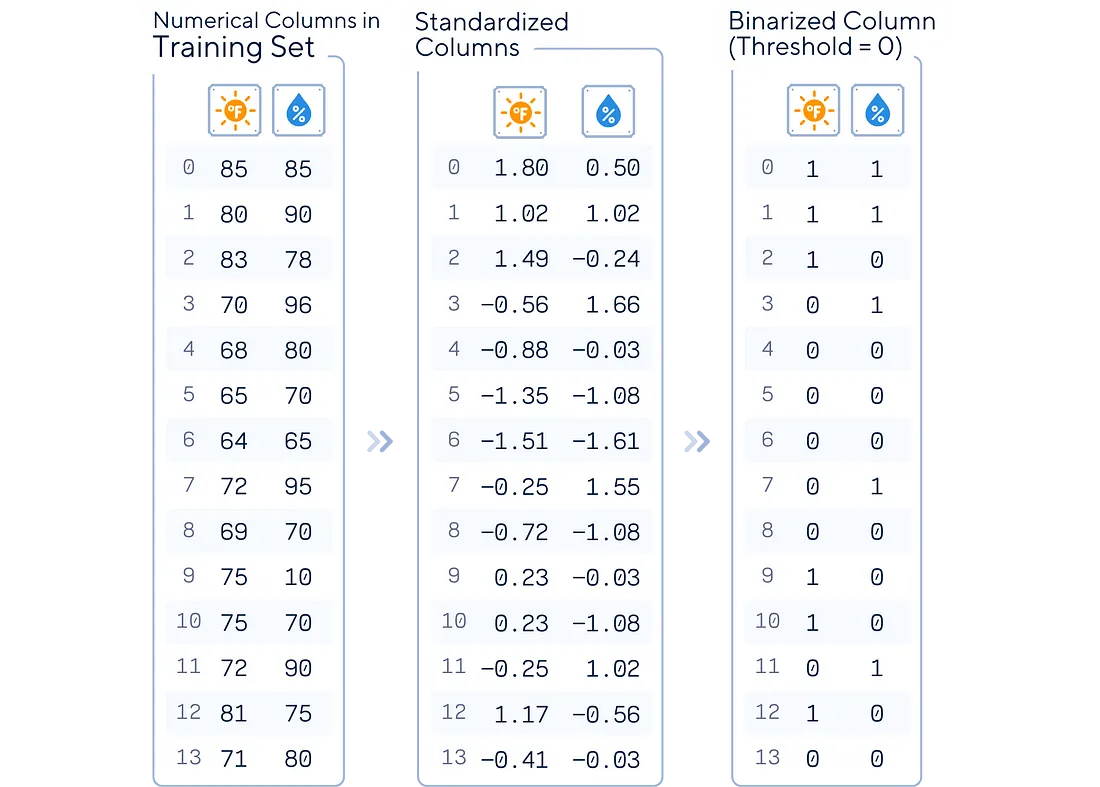
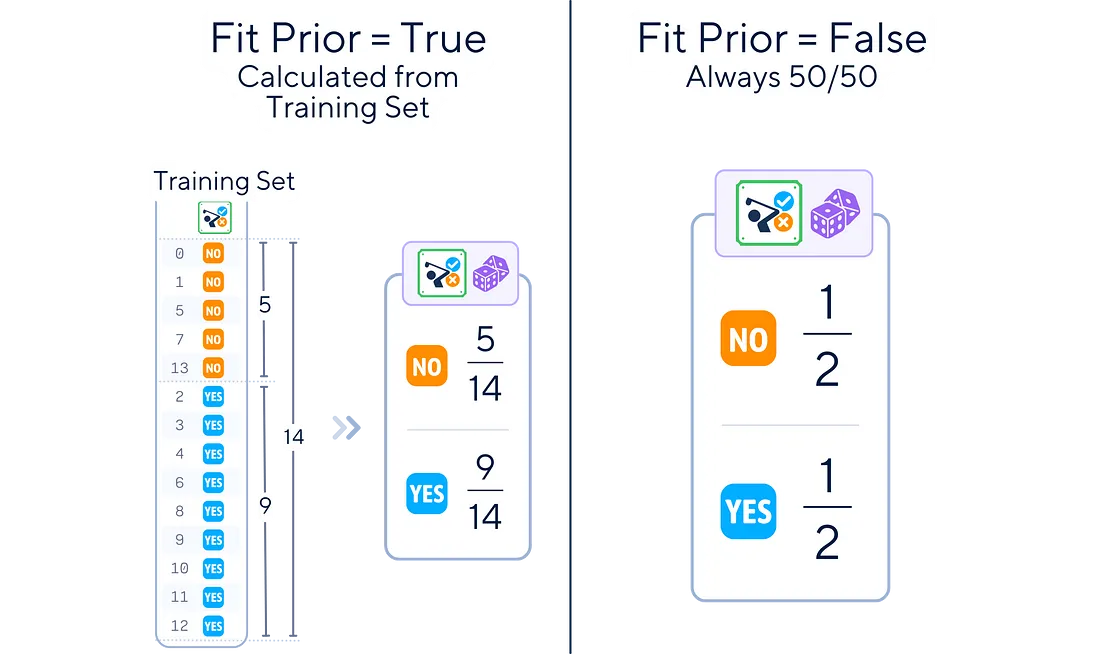
3.拟合先验：是否学习类先验概率或假设统一先验（50/50）。

对于我们的高尔夫数据集，我们可能从默认的 α=1.0 开始，不进行二值化（因为我们已经将我们的特征二值化），并且 fit_prior=True。

优点和缺点 与机器学习中的任何算法一样，伯努利朴素贝叶斯有其优点和局限性。 优点：

1. 简单：易于实现和理解。

2. 效率：训练和预测速度快，适用于大特征空间。

3. 小型数据集的性能：即使训练数据有限也能表现良好。

4. 处理高维数据：适用于许多功能，特别是在文本分类中。

缺点：

1. 独立性假设：假设所有特征都是独立的，但这在现实世界的数据中通常并不正确。

2. 仅限于二进制特征：纯形式仅适用于二进制数据。

3. 对输入数据的敏感性：对特征的二值化方式很敏感。

4. 零频率问题：如果没有平滑，零概率会严重影响预测。

结语 伯努利朴素贝叶斯分类器是一种简单但功能强大的二元分类机器学习算法。它在文本分析和垃圾邮件检测方面表现出色，这些分析中的特征通常是二元的。这种概率模型以速度快、效率高而闻名，在小数据集和高维空间中表现良好。 尽管它对特征独立性的假设很天真，但它的准确性往往可以与更复杂的模型相媲美。伯努利朴素贝叶斯是一种出色的基线和实时分类工具。 🌟 伯努利朴素贝叶斯简化版

# 导入所需库 import pandas as pd from sklearn.naive_bayes import BernoulliNB from sklearn.preprocessing import StandardScaler from sklearn.metrics import accuracy_score from sklearn.model_selection import train_test_split # 加载数据集 dataset_dict = { 'Outlook' : [ 'sunny' , 'sunny' , 'overcast' , 'rainy' , 'rainy' , 'rainy' , 'overcast' , 'sunny' , 'rainy' , 'sunny' , ' overcast' , 'rainy','sunny' , 'overcast' , 'rainy' , 'sunny' , 'overcast' , 'rainy' , 'sunny' , 'sunny' , 'rainy' , 'overcast' , 'rainy' , 'sunny' , '阴天' , '晴天' , '阴天' , '下雨' , '阴天' ], '温度' : [ 85.0 , 80.0 , 83.0 , 70.0 , 68.0 , 65.0 , 64.0 , 72.0 , 69.0 , 75.0 , 75.0 , 72.0 , 81.0 , 71.0 , 81.0 , 74.0 , 76.0 , 78.0 , 82.0 , 67.0 , 85.0 , 73.0 , 88.0 , 77.0 , 79.0 , 80.0 , 66.0 , 84.0 ], ‘湿度’：[ 85.0 , 90.0 , 78.0 , 96.0 , 80.0 , 70.0 , 65.0 , 95.0 , 70.0、80.0、70.0、90.0、75.0 、​​​​​​​ 80.0 , 88.0 , 92.0 , 85.0 , 75.0 , 92.0 , 90.0 , 85.0 , 88.0 , 65.0 , 70.0 , 60.0 , 95.0 , 70.0 , 78.0 ] , ' 风' : [假,真,假,假,假,假,真,假,假,假,真,假,假,真,假,假,假,假,假,假,假] , '播放' : [ '否' , '否' , '是' , '是' , '是' , '否' , '是' , '否' , '是','是' , '是' , '是' , '是' , '是' , '否' , '是', '否' , '是' , '是' , '否' , '否' , '是','是' , '否' , '否' , '是' , '是' , '是' , '是' , '是' , '是','是','是','是', '是' ] } df = pd.DataFrame(dataset_dict) # 为模型准备数据df = pd.get_dummies(df, columns=[ 'Outlook' ], prefix= '' , prefix_sep= '' , dtype= int ) df[ 'Wind' ] = df[ 'Wind' ].astype( int ) df[ '播放' ] = (df[ '播放' ] == '是' ).astype( int ) at_cols] = scaler.transform(X_test[float_cols]) # 训练模型 nb_clf = BernoulliNB() nb_clf.fit(X_train, y_train) # 进行预测 y_pred = nb_clf.predict(X_test) # 检查准确度 print ( f"Accuracy: {accuracy_score(y_test, y_pred)} " )

进一步阅读

感谢关注雲闪世界。（Aws解决方案架构师vs开发人员&GCP解决方案架构师vs开发人员）

订阅频道(https://t.me/awsgoogvps_Host) TG交流群(t.me/awsgoogvpsHost)