二阶专题
GNN-节点向量(Node Embedding)的表征学习-发展：随机游走/一阶二阶相似度(静态表征)【直接学习出各个节点的向量表示】 --＞图卷积(动态表征)【学习节点间聚合函数的参数】
静态表征 基于“随机游走”、“Word2vec”的：DeepWalk、Node2vec、Metapath2vec；基于“一阶相似度”、“二阶相似度”的：LINE、SDNE； 动态表征（GCN、GraphSAGE、GAT）【训练聚合函数的参数】
GNN-静态表征-随机游走-2014：DeepWalk【步骤：①随机游走策略生成每个节点的训练序列（DFS），得到训练数据集；②套用Word2vec算法得到节点表示】【捕获二阶相似度】【浅层、同质图】
一、概述 1、 2、DeepWalk、LINE、Node2vec对比 提出的顺序DeepWalk 2014, UNE 2015, Node2Vec 2016 Node2Vec设置 p = q = 1 p=q =1
双二阶滤波器之MATLAB设计及C语言实现
参考： 双二阶滤波器 本文中的例子和代码放在Github First，什么是双二阶滤波器？wiki上是这么说的：二阶、递归、线性，含有两个极点和两个零点，“双二阶”的名字来源于它的传递函数是两个二次多项式的比值。 In signal processing, a digital biquad filter is a second order recursive linear filter,
![[信号与系统]模拟域中的一阶低通滤波器和二阶滤波器](https://img-blog.csdnimg.cn/direct/8b2c16cd5f084d8a9a6eba3c68107ed8.png)
[信号与系统]模拟域中的一阶低通滤波器和二阶滤波器
前言 不是学电子出身的，这里很多东西是问了朋友… 模拟域中的一阶低通滤波器传递函数 模拟域中的一阶低通滤波器的传递函数可以表示为： H ( s ) = 1 s + ω c H(s) = \frac{1}{s + \omega_c} H(s)=s+ωc1 这是因为一阶低通滤波器的设计目标是允许低频信号通过，同时衰减高频信号。具体来说，它的频率响应特性决定了这个形式的传递函数。 1.
second order system analysis in adaptive control 自控 带零点的二阶系统matlab仿真分析
带零点的二阶系统matlab仿真分析 上图是使用Matlab的simulink对带零点的二阶系统模型和不带零点的二阶系统进行仿真分析的模拟图 仿真示波器输出结果： 上面的波形是带零点的二阶系统输出 下面的波形是不带零点的二阶系统的波形输出 我们可以看出，零点(位于实轴负半轴)对二阶系
second order system analysis 自动控制原理 二阶系统的matlab仿真分析
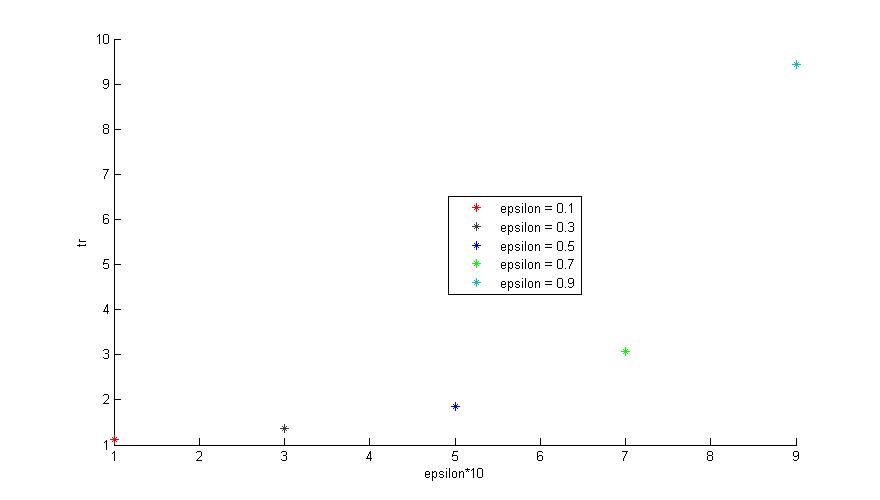
二阶系统的matlab仿真分析 二阶系统的matlab仿真分析如上图。 根据二阶函数对阶跃函数的响应函数，我们对参数epsilon进行分析讨论 由于临界阻尼和无阻尼的情况在现实生活中比较难出现，二阶方程的根几乎不可能恰好，实部为0，或者两个实部相同且虚部为0. 于是，并为对以上两种较特殊的情况进行讨
一般二阶线性非齐次微分方程的解与对应齐次方程的解的关系
一般二阶线性非齐次微分方程的解与对应齐次方程的解的关系 @(微积分) 设 p(x),q(x),f(x),f(x)≠0 p(x),q(x),f(x),f(x)\neq 0为连续函数，对于下面的二阶线性非齐次方程： y″+p(x)y′+q(x)y=f(x) y''+p(x)y'+q(x)y = f(x) (1) 对应的二阶线性齐次方程： y″+p(x)y′+q(x)y=0 y''+p(x
一阶矩+二阶矩估计求解一个参数
一阶矩+二阶矩估计求解一个参数 @(概率论) 一般来说，一个参数对应一个方程。所以在矩估计法中，用一阶矩就可以求解一元。但是有些情况下，只写一阶矩，原理上是可以求得解的，但是，初等代数中很难剥离出来，可以考虑再求一次二阶矩，即，再利用样本提供一组值，二者相互作用，可以求解出p. 值得注意的是，二者求得的实际解并不是完全一致，因为又一次用了矩估计，所以等于两次估计求解一元。这是可以接受的，因为
由二阶常系数线性方程的通解反推方程
由二阶常系数线性方程的通解反推方程 @(微积分) 引例是这样的： 设 cosx cosx与 xex xe^x为某n阶常系数线性齐次方程的两个解，则最小的n = ？，相应的首项系数为1的方程是？ 分析：由cosx是一个解，则必有另一解sinx, ±i \pm i是它的特征根； xex xe^x是一个解，则必有另一解 ex e^x,则1必是二重特征根。所以，n至少为4.特征方程可以列举如
Beamer中二阶导、一阶导数的显示问题
Beamer中二阶导、一阶导数的显示问题 解决方法: 最简单的解法方法就是把\documentclass[professionalfont]{beamer} 改为 \documentclass[professionalfont]{beamer} 如果不能解决、请继续阅读查看其他解法 在beamer中表示 f ′ f' f′和 f ′ ′ f'' f′′时发现导数符号距离 f f
华为开源自研AI框架昇思MindSpore应用案例：在ResNet-50网络上应用二阶优化实践
常见的优化算法可分为一阶优化算法和二阶优化算法。经典的一阶优化算法如SGD等，计算量小、计算速度快，但是收敛的速度慢，所需的迭代次数多。而二阶优化算法使用目标函数的二阶导数来加速收敛，能更快地收敛到模型最优值，所需要的迭代次数少，但由于二阶优化算法过高的计算成本，导致其总体执行时间仍然慢于一阶，故目前在深度神经网络训练中二阶优化算法的应用并不普遍。二阶优化算法的主要计算成本在于二阶信息矩阵（He
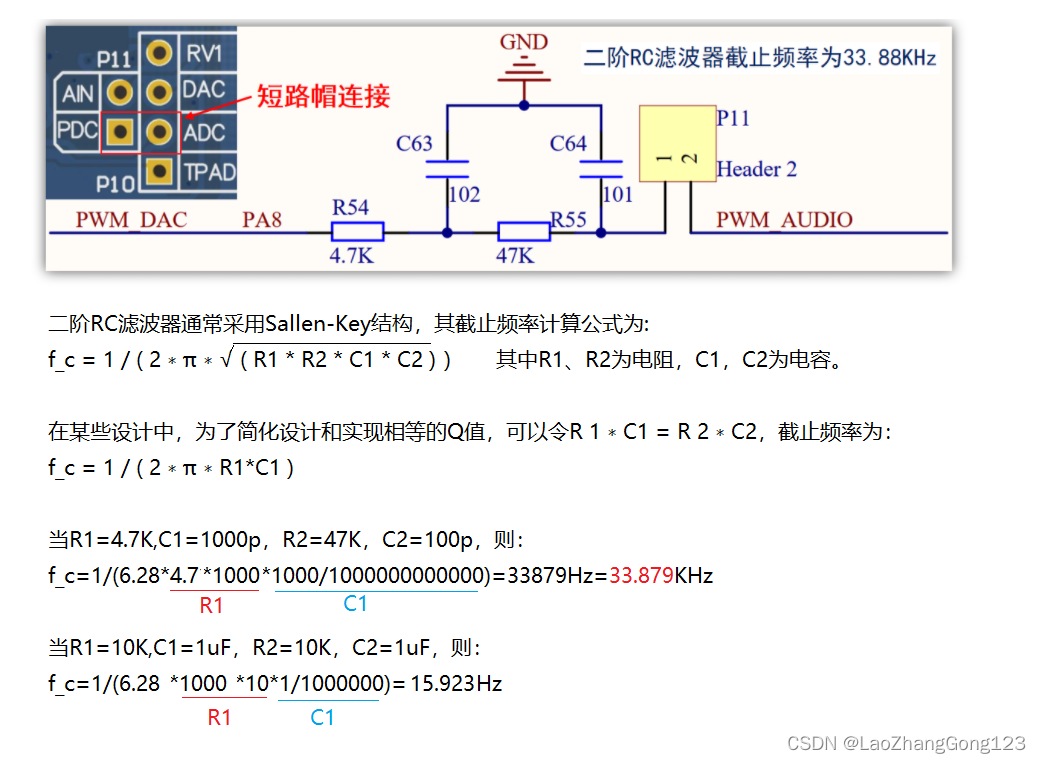
二阶RC滤波器截止频率计算
f_c = 1 / ( 2 ∗ π ∗ √ ( R 1 ∗ R 2 ∗ C1*C2 ) ),其中R1、R2为电阻，C1,C2为电容。在某些设计中，为了简化设计和实现相等的Q值，可以令R 1 ∗ C1 = R 2 ∗ C2，这时截止频率简化为 f_c = 1 / ( 2 ∗ π ∗ R1*C1 ) 当R1=4.7K,C1=1000p，R2=47K，C2=100p，则f_c=1/(6.28*470
Matlab|二阶锥松弛在配电网最优潮流计算中的应用
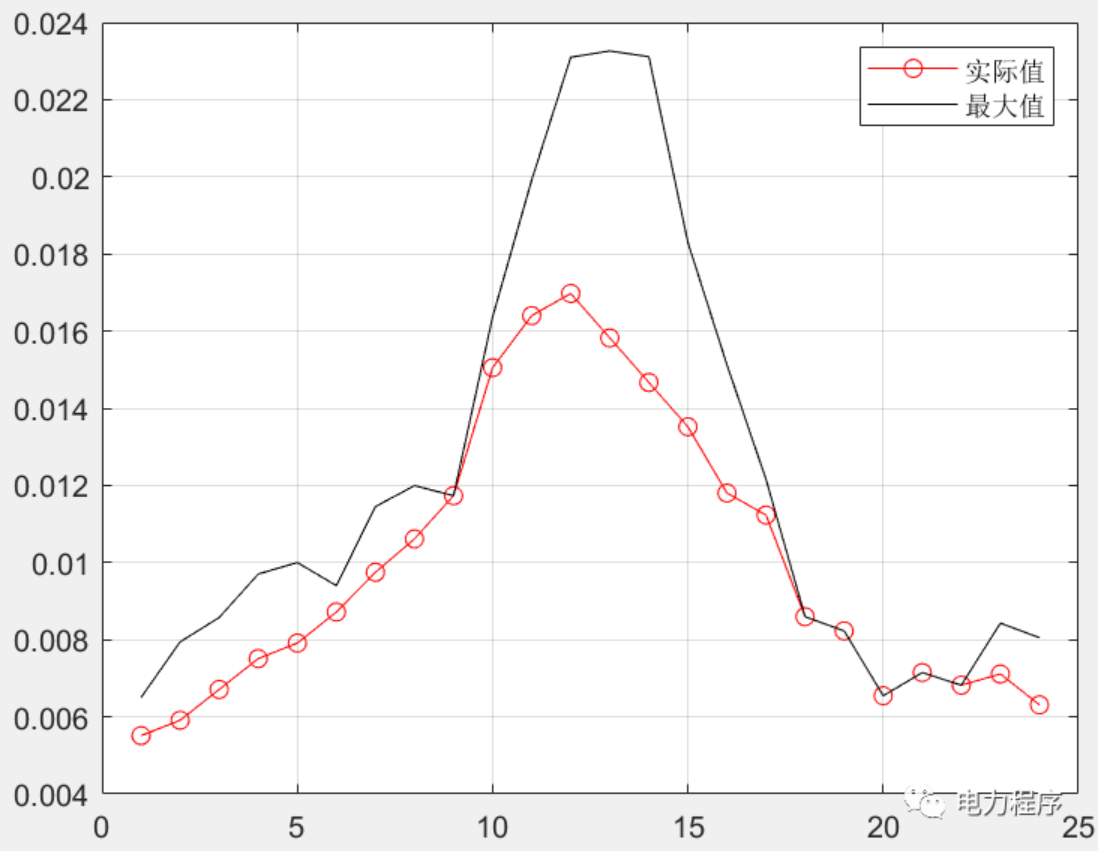
目录 一、主要内容 二、部分代码 三、程序代码 四、下载链接 一、主要内容 最优潮流计算是电网规划、优化运行的重要基础。首先建立了配电网全天有功损耗最小化的最优潮流计算模型；其次结合辐射型配电网潮流特点建立支路潮流约束，并考虑配电网中的可控单元，包括分布式电源和离散、连续无功补偿装置，建立其出力约束，该模型为非凸非线性模型；然后通过二阶锥松弛将该模型转化为包含整数变量的二阶
偏微分方程算法之二阶双曲型方程交替方向隐格式
目录 一、研究目标 二、理论推导 2.1 显差分格式 2.2 交替方向隐格式 三、算例实现 四、结论 一、研究目标 本节的研究对象为如下的双曲型偏微分方程初边值问题： 为了保证连续性，公式（1）中相关函数满足： 二、理论推导 2.1 显差分格式 第一步：网格剖分。在三维长方体空间（二维平面加一维时间轴）进行网格
C++心决之类和对象详解(中篇)(封装入门二阶)
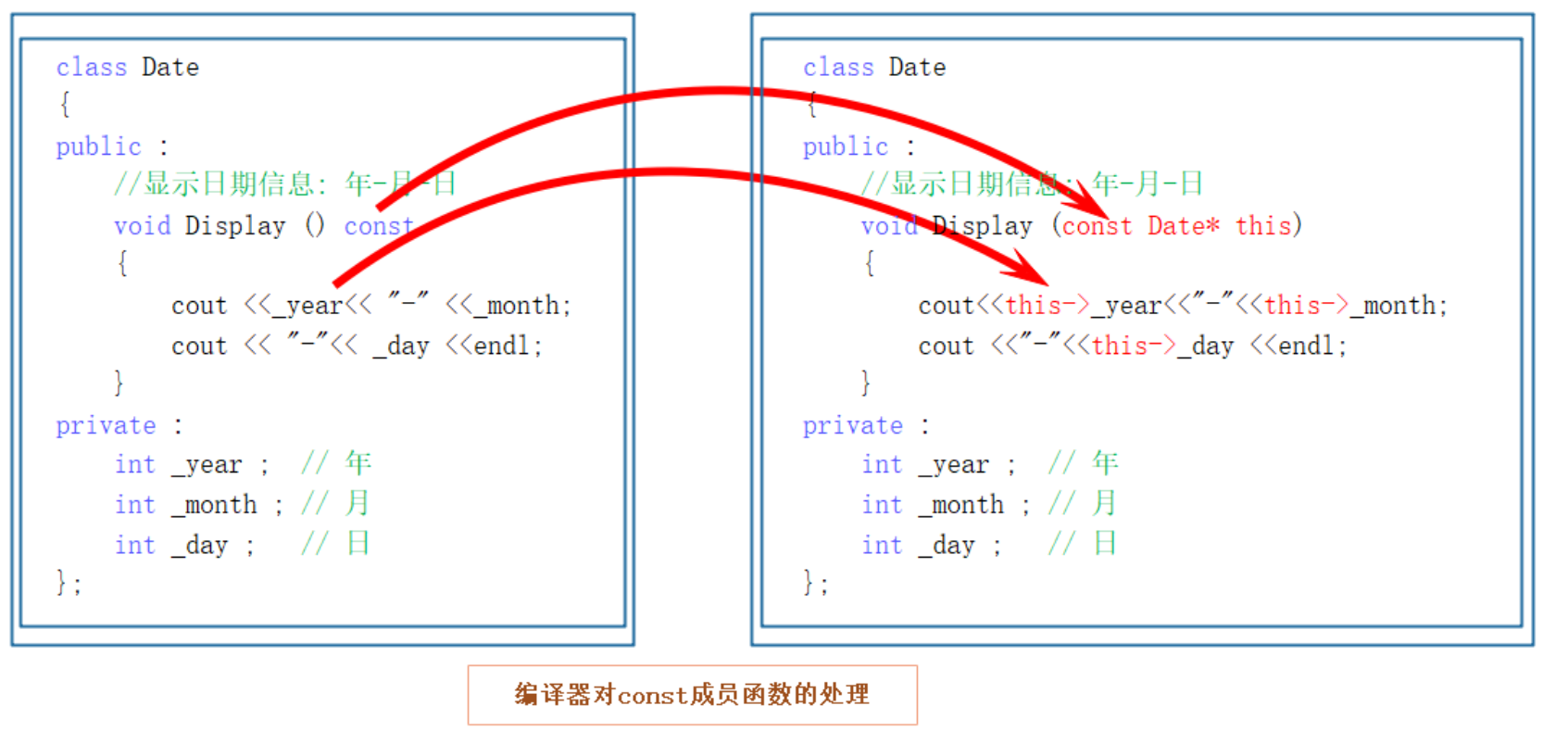
目录 1.类的6个默认成员函数 2. 构造函数 2.1 概念 2.2 特性 3.析构函数 3.1 概念 3.2 特性 4. 拷贝构造函数 4.1 概念 4.2 特征 5.赋值运算符重载 5.1 运算符重载 5.2 赋值运算符重载 5.3 前置++和后置++重载 7.const成员 8.取地址及const取地址操作符重载 1.类的6个默认成员函数
偏微分方程算法之二阶双曲型方程紧差分方法
目录 一、研究目标 二、理论推导 三、算例实现 一、研究目标 前面我们已经介绍了二阶双曲型方程显式、隐式差分格式，可否像抛物型方程一样，构建更高精度的差分格式。接下来我们介绍紧差分格式。这里继续以非齐次二阶双曲型偏微分方程的初边值问题为研究对象： 公式（1）中u表示一个与时间t和位置x有关的待求波函数，及方程右端项函数都是已知函数，是非零常数。 二、理论推导
hibernate进二阶之各式查询
hibernate.cfg.xml <!DOCTYPE hibernate-configuration PUBLIC"-//Hibernate/Hibernate Configuration DTD 3.0//EN""http://www.hibernate.org/dtd/hibernate-configuration-3.0.dtd"><hibernate-configuration><
hibernate进二阶之理解二级缓存
Hibernate提供了基于应用程序级别(进程)的缓存， 可以跨多个session，即不同的session都可以访问缓存数据。 这个换存也叫二级缓存。 Hibernate提供的二级缓存有默认的实现，且是一种可插配的缓存框架！如果用户想用二级缓存，只需要在hibernate.cfg.xml中配置即可； 不想用，直接移除，不影响代码。 hibernate.cfg.xml <!--**
hibernate进二阶之项目中session的管理方式
@Testpublic void testSession() throws Exception {//openSession: 创建Session, 每次都会创建一个新的sessionSession session1 = sf.openSession();Session session2 = sf.openSession();System.out.println(session1 == sess
c++类构造函数—二阶构造法
为什么要用二阶构造？ 当类的成员比较简单，如只有赋值等简单操作时，普通的构造函数就可以。 然而实际中，以面向对象的思维开发程序时，类往往十分复杂，设计到动态内存申请、文件打开等操作。然而在调用构造函数后，无法得知这些复杂的操作是否顺利完成。假若动态内存未成功申请，然而对象实例在主程序中依然成功创建，这样的对象称为半成品对象。在后续对该对象的操作，往往会引起程序的奔溃。 为了防止出现这样的情况，
基于JAX的二阶优化方法的实践
使用协作分支上的算法 git clone https://github.com/linjing-lab/jax.gitcd jaxgit checkout linjing-labcd examples 在命令行预览方法 牛顿方法： cat newton_method.py 拟牛顿法： cat bfgs_method.py 在命令行运行程序 python newton_m
高斯分布归一化、期望、二阶矩、方差推导证明
目录 写在前面的唠叨： 归一化推导证明： 期望（一阶矩）推导证明： 二阶矩推导证明： 方差推导证明： 写在前面的唠叨： 最近这段时间一直在研究深度学习之类的东西，虽然如今对几种常见的神经网络都有了很好的了解，用起来也比较顺手，但是越学也越觉得瓶颈越来越明显了，最大的问题觉得还是数学基础不行，学习那些常见的模型已经把线性代数的知识捡的差不多了，而到了想自己设计模型的时候，才忽
汽车控制器基于Simulink模型开发MBD常用滤波器设计系列课程连载之二（下）: 二阶高通、带通、带阻滤波器建模及测试验证
[睿创智能科技]汽车控制器基于Simulink模型开发MBD常用滤波器设计系列课程连载之二（下）: 二阶高通、带通、带阻滤波器建模及测试验证