Matlab|二阶锥松弛在配电网最优潮流计算中的应用

本文主要是介绍Matlab|二阶锥松弛在配电网最优潮流计算中的应用，希望对大家解决编程问题提供一定的参考价值，需要的开发者们随着小编来一起学习吧！

一、主要内容

二、部分代码

三、程序代码

四、下载链接

一、主要内容

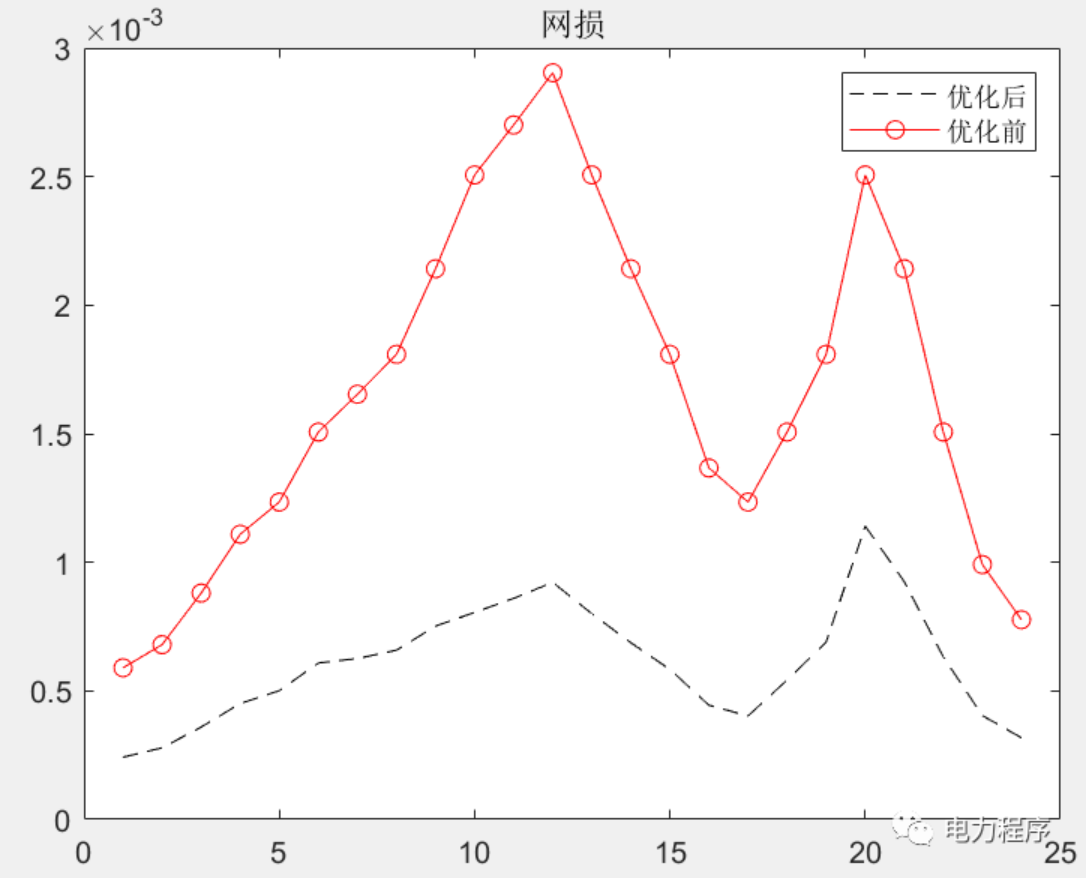
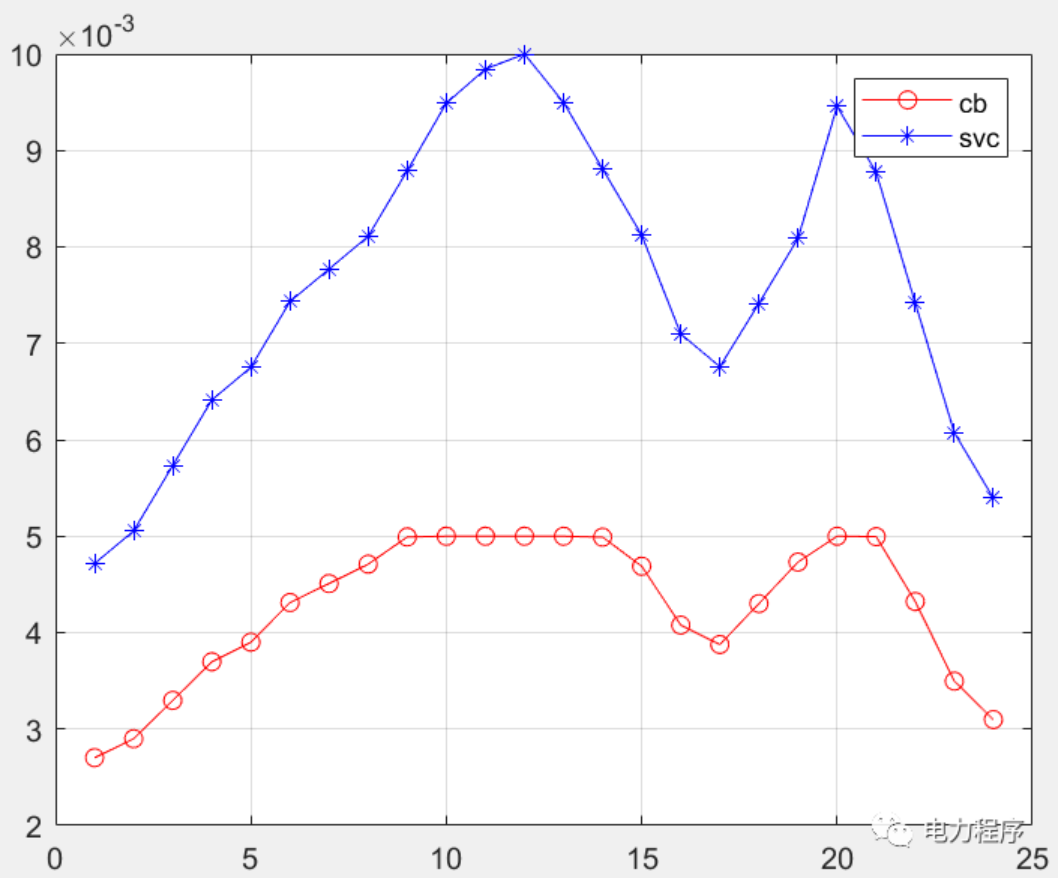
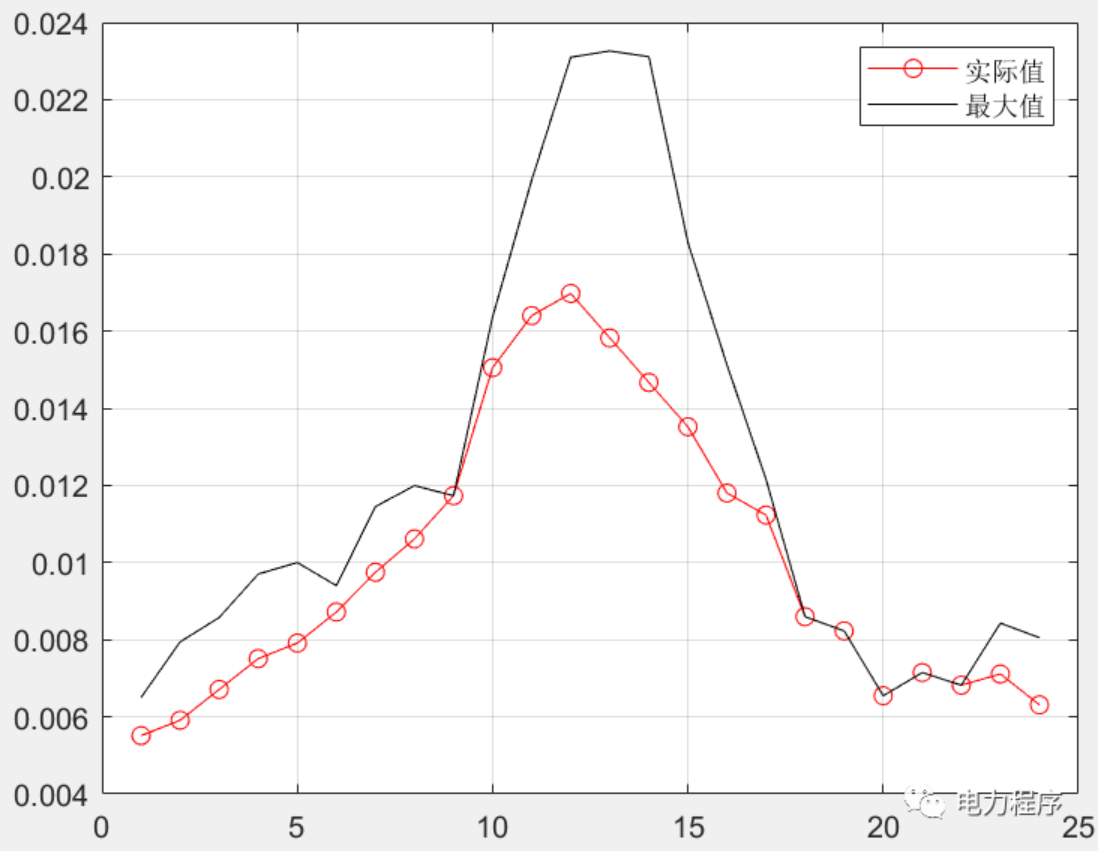
最优潮流计算是电网规划、优化运行的重要基础。首先建立了配电网全天有功损耗最小化的最优潮流计算模型；其次结合辐射型配电网潮流特点建立支路潮流约束，并考虑配电网中的可控单元，包括分布式电源和离散、连续无功补偿装置，建立其出力约束，该模型为非凸非线性模型；然后通过二阶锥松弛将该模型转化为包含整数变量的二阶锥规划模型。

二、部分代码

%% 1.设参
mpc = IEEE33BW;
pload = mpc.Pload;%节点有功负荷
qload = mpc.Qload;%节点无功负荷
branch = mpc.branch;
branch(:,3) = branch(:,3)*100/(12.66^2);%求阻抗标幺值
r = real(branch(:,3));
x = imag(branch(:,3));
T = 24;%时段数为24小时
nb = 33;%节点数
nl = 32;%支路数
pw=[45.56 55.67 60.09 67.99 70.08 65.88 69.75 65.88 55.08 50.34 56.32 60.44 57.90 60.88 45.40 40.71 21.44 27.59 29.08 45.88 50.09 47.80 59.07 56.42];
%光伏发电预测：
pv=[0 0 0 0 0 0 5.80 10.04 15.00 35.56 45.99 56.06 58.09 55.87 45.77 36.08 35.23 18.04 15.79 0 0 0 0 0 ];

upstream = zeros(nb,nl);
dnstream = zeros(nb,nl);
for i = 1:nlupstream(i,i) = 1;
end
for i=[1:16,18:20,22:23,25:31]dnstream(i,i+1) = 1;
end
dnstream(1,18) = 1;
dnstream(2,22) = 1;
dnstream(5,25) = 1;
dnstream(33,1) = 1;

Vmax = [1.05*1.05*ones(nb-1,T)1.05*1.05*ones(1,T)];
Vmin = [0.95*0.95*ones(nb-1,T)1.05*1.05*ones(1,T)];
Pgmax = [zeros(nb-1,T)ones(1,T)];
Qgmax = [zeros(nb-1,T)ones(1,T)];
%% 2.设变量
V = sdpvar(nb,T);%电压的平方
I = sdpvar(nl,T);%电流的平方
P = sdpvar(nl,T);%线路有功
Q = sdpvar(nl,T);%线路无功
Pg = sdpvar(nb,T);%发电机有功
Qg = sdpvar(nb,T);%发电机无功
gf8=sdpvar(1,T);%节点8光伏
fd12=sdpvar(1,T);%节点12风电
cb18=sdpvar(1,T);%节点18
svc31=sdpvar(1,T);%节点31