松弛专题
【机器学习】基于Softmax松弛技术的离散数据采样
1.引言 1.1.离散数据采样的意义 离散数据采样在深度学习中起着至关重要的作用,它直接影响到模型的性能、泛化能力、训练效率、鲁棒性和解释性。 首先,采样方法能够有效地平衡数据集中不同类别的样本数量,使得模型在训练时能够更均衡地学习各个类别的特征,从而避免因数据不平衡导致的偏差。 其次,合理的采样策略可以确保模型在训练过程中能够接触到足够多的样本,避免过拟合和欠拟合问题,提高模型的泛化能力
大历史下的 tcp:一个松弛的传输协议
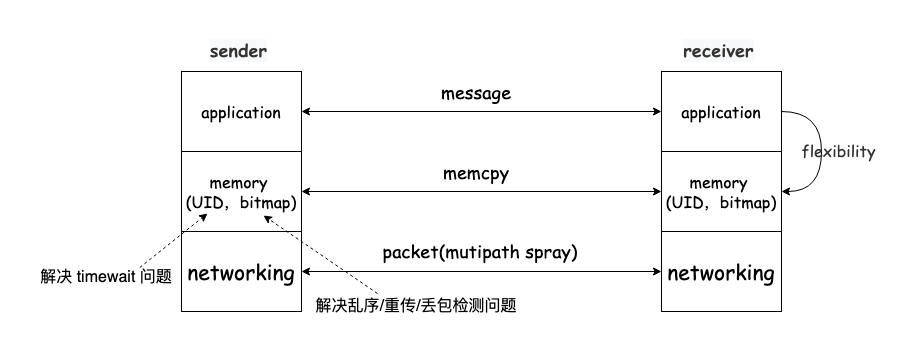
如果 tcp 是一个相对松弛的协议,会发生什么。 所谓松弛感,意思是它允许 “漏洞”,允许可靠传输的不封闭,大致就是:“不求 100% 可靠,只要 90%(或多或少) 可靠,另外 10% 的错误可检测到” or “不实现 100% 可靠逻辑,只负责 99%(或多或少) 大概率事件,忽略 1% 的小概率事件,由上层协议处理或不处理”。 前文谈到 tcp timewait,我说只需一个按连接递增的
Matlab|二阶锥松弛在配电网最优潮流计算中的应用
目录 一、主要内容 二、部分代码 三、程序代码 四、下载链接 一、主要内容 最优潮流计算是电网规划、优化运行的重要基础。首先建立了配电网全天有功损耗最小化的最优潮流计算模型;其次结合辐射型配电网潮流特点建立支路潮流约束,并考虑配电网中的可控单元,包括分布式电源和离散、连续无功补偿装置,建立其出力约束,该模型为非凸非线性模型;然后通过二阶锥松弛将该模型转化为包含整数变量的二阶
成都爱尔谭娇解读眼睑松弛“提拉”要趁早,避免遮挡损害视力!
眼皮耷拉无力没法抬起,仿佛永远没睡醒。 怎么使力都没用眼睛就是睁不开, 甚至两只眼睛一大一小不对称, 这种时候要警惕一种病症“上睑下垂”! 早期上睑下垂症状并不明显,很容易被忽视,但眼睑下垂时间久了可能会对视力产生影响。成都爱尔眼科医院眼整形科谭娇主任为大家带来讲解。 什么是上睑下垂? 上脸下垂是指由于上脸肌肉功能不全或丧失以致上眼皮呈现部分或全部下垂。但并
贪心算法-4.5单源最短路径之Dijkstra算法(松弛操作)
问题描述:对下图中的有向图,应用Dijkstra算法计算从源顶点1到其他顶点间最短路径的过程列在下页的表中。 问题分析: public class test4_5 {public static void Dijkstra(int v,float[][] a,float[] dist,int[] prev){int n = dist.length;if(v<0||v>n-1) retur
离散优化模型的松弛模型
在分支定界算法中(常用来求解离散优化问题),我们求节点问题的最优界时,往往需要求解节点问题的松弛问题的最优解,那么这个所谓的松弛问题是什么呢? 顾名思义,就是将原问题的部分约束条件进行丢弃或放宽,而对离散优化模型而言,口头上的松弛问题常常指的是线性松弛问题,即将整数规划问题中的约束条件中的整数要求放宽,整数变量改为实数变量,将原整数规划问题转化为一个线性规划问题。 min c x s .
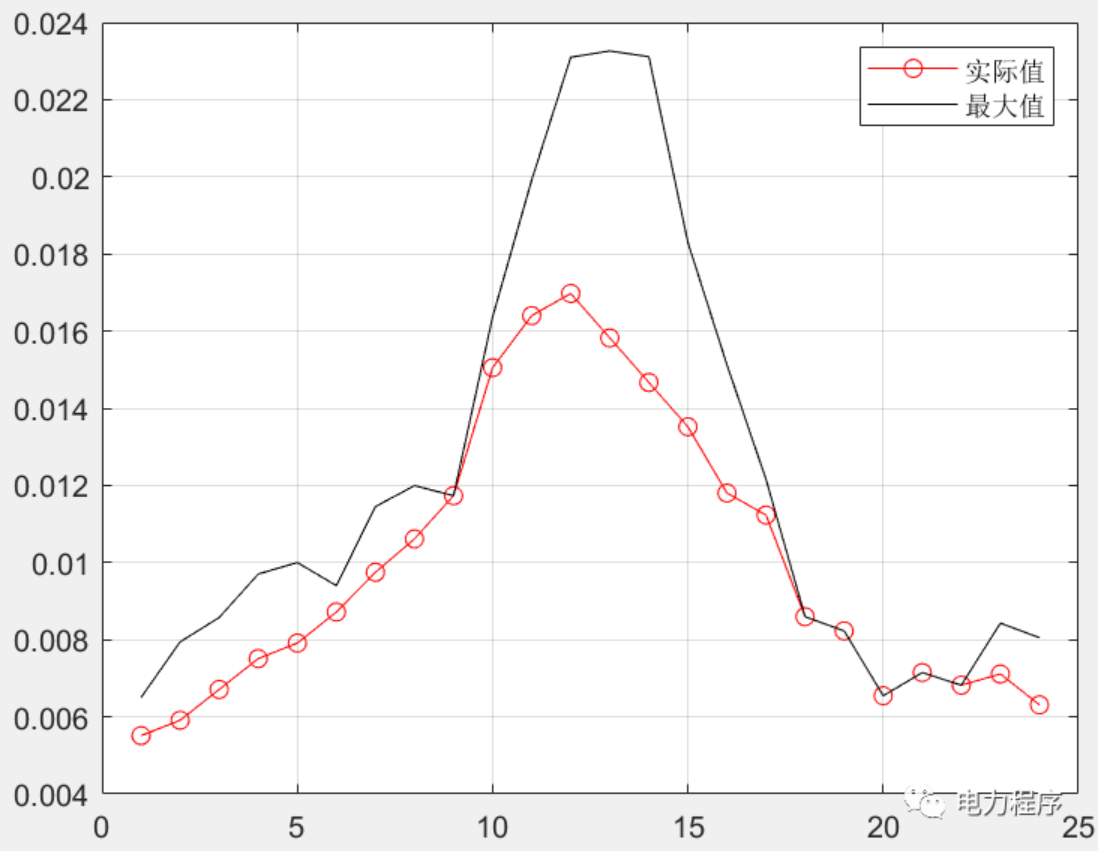
节点电力市场生产商的战略竞标:凸松弛方法(Matlab实现)
目录 1 电力市场 1.1 什么是电力市场 1.2 电力市场发展历程 1.3 对传统电力系统理论的挑战 2 节点电力市场生产商的战略竞标:凸松弛方法 2.1 简介 2 Matlab代码 所有专栏和电气论文代码目录都在这篇文章:电力系统与算法之美(Python&Matlab代码) 1 电力市场 1.1 什么是电力市场 市场:商品交换(交换商品的过程称交易)
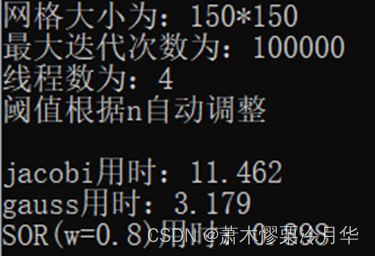
C++多线程下分别使用雅各比迭代法、高斯赛德尔迭代法、逐次超松弛迭代法解决稳态热传导问题,使用Python数据可视化
稳态导热,稳态导热是物体的温度不随时间而变化的导热过程。稳态热传导问题在这里被模拟为,对于一个n*n的网格,对其某个位置持续给定初始温度,求解最终的稳态导热状态,稳态热传导问题即求解最终的稳态温度。 温度网格示例如下: 正确解决温度热传导问题后得到的温度图像类似于下图所示: 问题拟定 对于n*n的网格,初始温度全部为0,给其上边与右边的中部位置持续给定大小为1的热度,
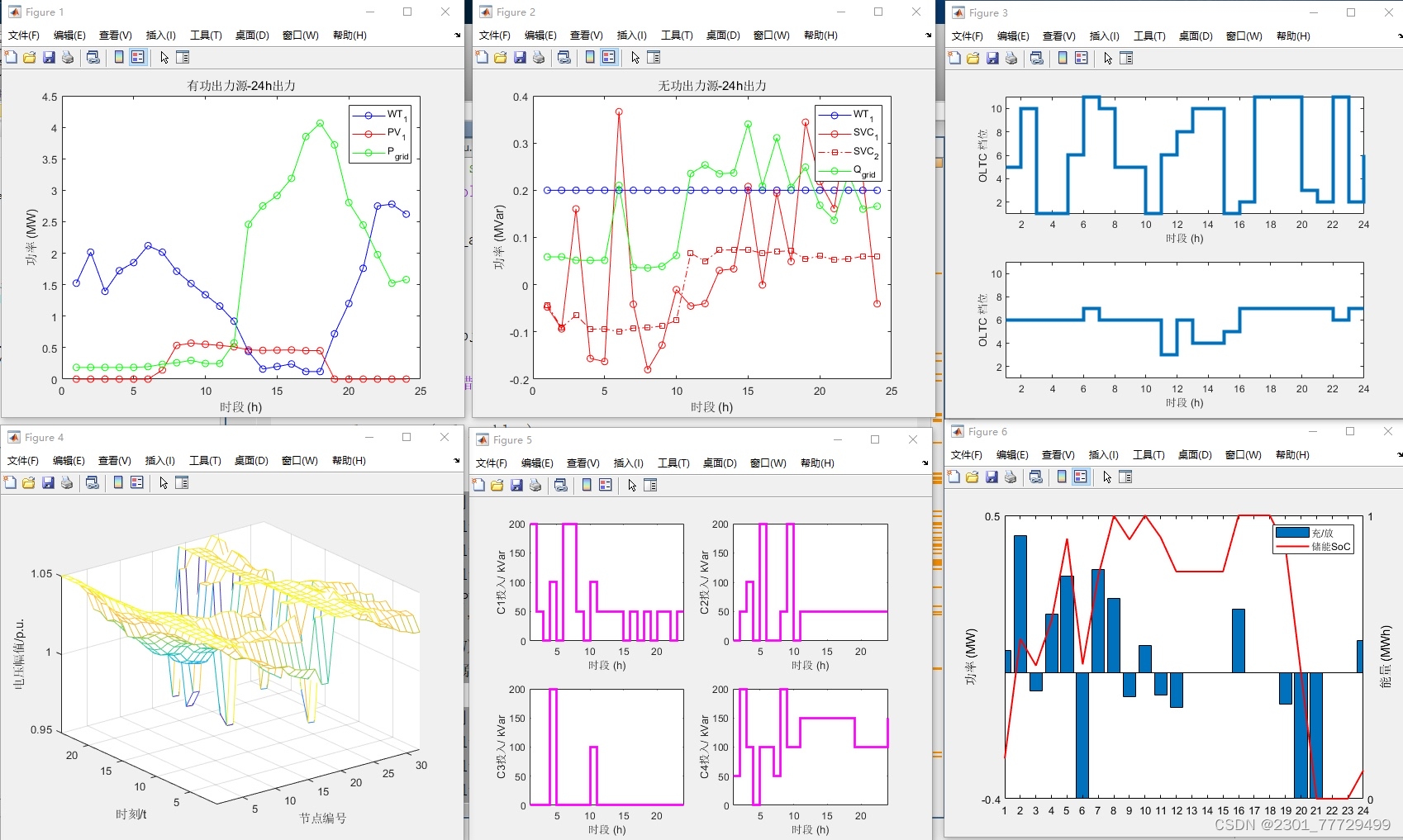
二阶锥松弛化的无功优化代码 考虑储能系统ESS,有载调压分接头OLTC,离散电容器CB和静止无功补偿SVC设备约束
二阶锥松弛化的无功优化代码 考虑储能系统ESS,有载调压分接头OLTC,离散电容器CB和静止无功补偿SVC设备约束 以购电和网损成本最小为目标 采用IEEE 33节点算例仿真 使用二阶锥松弛将模型线性化 使用yalmip-cplex gurobi求解器编写 ID:45100671440106005
二阶锥松弛化的无功优化代码考虑储能系统ESS,有载调压分接头OLTC,离散电容器CB和静止无功补偿SVC设备约束
二阶锥松弛化的无功优化代码 考虑储能系统ESS,有载调压分接头OLTC,离散电容器CB和静止无功补偿SVC设备约束 以购电和网损成本最小为目标 采用IEEE 33节点算例仿真 使用二阶锥松弛将模型线性化 使用yalmip-cplex gurobi求解器编写 储能系统ESS(Energy Storage System)是近年来备受关注的技术,它不仅能够提高电网的稳定性,还能够减少峰谷差,提高电
人工智能_机器学习061_KKT条件公式理解_原理深度解析_松弛变量_不等式约束---人工智能工作笔记0101
然后我们再来看,前面我们,拉格朗日乘子法,把带有条件的,问题,优化成了等式问题,从而, 构建拉格朗日乘子公式,进行实现了求解,但是在现实生活中,往往也有,很多不等式问题. 比如上面的这个,就是要求是h(x)<=0的情况下,函数f(x)的最小值. 可以看到,这个带有一个不等式的条件,那么这种的如何求呢 我们可以回去看看拉格朗日乘子法的公式,可以看到是一个等式条件,这个时候可以,引
ICCV 2021 | 松弛Transformer:实现直接出框的时序动作检测
本文介绍我们组在2021年初公开在arxiv上的时序动作候选框生成工作RTD (Relaxed Transformer Decoders for Direct Action Proposal Generation)。 论文链接:https://arxiv.org/abs/2102.01894 代码地址:https://link.zhihu.com/?target=https%3A//githu
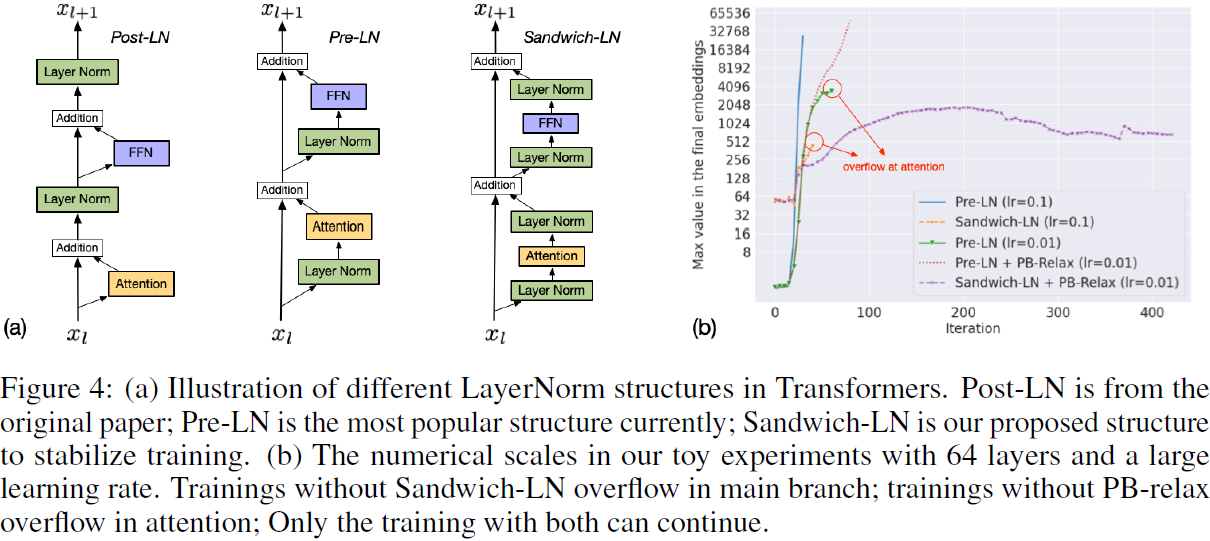
(2021|NIPS,VQ-VAE,精度瓶颈松弛,三明治层归一化,CapLoss)CogView:通过转换器掌握文本到图像的生成
CogView: Mastering Text-to-Image Generation via Transformers 公众号:EDPJ(添加 VX:CV_EDPJ 或直接进 Q 交流群:922230617 获取资料) 目录 0. 摘要 1. 简介 2. 方法 2.1 理论 2.2 标记化 2.3 自回归 Transformer 2.4 训练的稳定性 3. 微调 3.
【运筹优化】拉格朗日松弛 次梯度算法求解整数规划问题 + Java调用Cplex实战
文章目录 一、拉格朗日松弛二、次梯度算法三、案例实战 一、拉格朗日松弛 当遇到一些很难求解的模型,但又不需要去求解它的精确解,只需要给出一个次优解或者解的上下界,这时便可以考虑采用松弛模型的方法加以求解。 对于一个整数规划问题,拉格朗日松弛放松模型中的部分约束。这些被松弛的约束并不是被完全去掉,而是利用拉格朗日乘子在目标函数上增加相应的惩罚项,对不满足这些约束条件的解进行惩
Dijkstra算法——通过边实现松弛
引入: 指定一个点(源点)到其余各个顶点的最短路径,也叫做“单源最短路径”。例如求下图中的1号顶点到2、3、4、5、6号顶点的最短路径。 一如既往,二维数组存图: 但是,我们还需要一个一维数组dis来存储1号顶点到其余各个顶点的初试路程。如下: 我们将此时dis数组中的值称为最短路程的“估计值”。 既然是求1号顶点到其余各个顶点的最短路程,那就先找一个离1号顶点最近的
java调用cplex实现拉格朗日松弛算法求解整数规划问题
拉格朗日松弛算法 在难以求解的模型当中,可以使用分支定界算法,割平面算法等算法进行精确求解,以便于获得问题的精确解。若在求解过程中,这些难以求解的模型不需要获得他的精确解,而是只需要给出一个次优解或者解的上下界。在这种情况下可以考虑采用松弛模型的方法。当然,智能算法也是一种解决途径。 对于一个整数规划问题,与0-1整数规划问题中将离散变量的取值范围松弛为[0,1]之间的连续变量不同,拉格朗日松
(2021|NIPS,VQ-VAE,精度瓶颈松弛,三明治层归一化,CapLoss)CogView:通过转换器掌握文本到图像的生成
CogView: Mastering Text-to-Image Generation via Transformers 公众号:EDPJ(添加 VX:CV_EDPJ 或直接进 Q 交流群:922230617 获取资料) 0. 摘要 通用领域中的文本到图像生成长期以来一直是一个悬而未决的问题,这需要强大的生成模型和跨模态理解。 我们提出了 CogView,一个具有 VQ-VAE 标记器的