Dijkstra算法——通过边实现松弛

引入：

指定一个点（源点）到其余各个顶点的最短路径，也叫做“单源最短路径”。例如求下图中的1号顶点到2、3、4、5、6号顶点的最短路径。

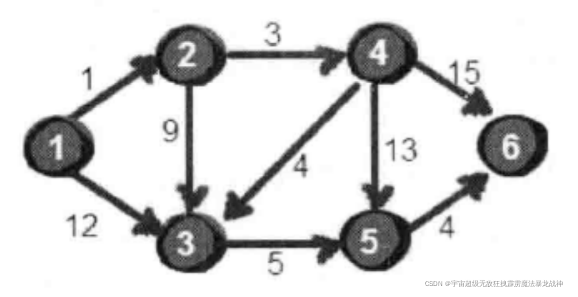
一如既往，二维数组存图：

但是，我们还需要一个一维数组dis来存储1号顶点到其余各个顶点的初试路程。如下：

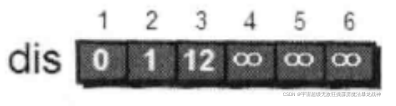
我们将此时dis数组中的值称为最短路程的“估计值”。

既然是求1号顶点到其余各个顶点的最短路程，那就先找一个离1号顶点最近的顶点。通过数组dis可知当前离1号顶点最近的是2号顶点。当选择了2号顶点后，dis[2]的值就已经从“估计值”变为了“确定值”，即1号顶点到2号顶点的最短路程就是当前dis[2]值；

松弛2号顶点：

既然选择了2号顶点，接下来再来看2号顶点有哪些出边呢。有2-->3和2-->4这两条边。先讨论通过2-->3这条边能否让1号顶点到3号顶点的路程变短，也就是说现在来比较dis[3]和dis[2]+e[2][3]的大小。其中dis[3]表示1号顶点到3号顶点的路程；我们发现dis[3] = 12，dis[2] + e[2][3] = 1 + 9 = 10,dis[2] + e[2][3] < dis[3],因此dis[3]要更新为10。这个过程有个专业术语叫做“松弛”，1号顶点到3号顶点的路程变为dis[3]，通过2-->3这条边松弛成功。

这便是Dijkstra算法的主要思想：通过“边”来松弛1号顶点到其余各个顶点的路程。

同理，通过2-->4（e[2][4]），可以将dis[4]的值从 oo 松弛为4(dis[4]初始为oo，dis[2] + e[2][4] = 1 + 3 = 4)，dis[2] + e[2][4] < dis[4]，因此dis[4]要更新为4）。

刚才我们对2号顶点所有的出边进行了松弛。松弛完毕之后dis数组为：

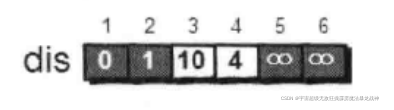
接下来，继续在剩下的3、4、5和6号顶点中，选出离1号顶点最近的顶点。通过上面更新过的dis数组，当前离1号顶点最近的是4号顶点。此时，dis[4]的值已经从“估计值”变为了“确定值”。

松弛4号顶点：

下面继续对4号顶点的所有出边（4-->3，4-->5和4-->6）用刚才的方法进行松弛。松弛完毕之后dis数组为：

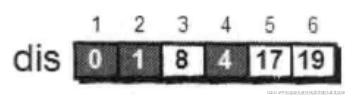
 继续在剩下的3、5和6号顶点中，选出离1号顶点最近的顶点，那就是3号顶点；

松弛3号顶点：

对3号顶点的所有出边（3-->5）进行松弛。松弛完毕之后dis数组为：

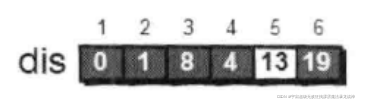
继续在剩下的5和6号顶点中，选出离1号顶点最近的顶点，这次选择5号顶点。此时，dis[5]的值已经从“估计值”变为了“确定值”。

松弛5号顶点：

对5号顶点的所有出边（5-->4）进行松弛。松弛完毕之后dis数组为：

最后对6号顶点的所有出边进行松弛。因为这个例子中6号顶点没有出边，因此不用处理。到此，dis数组中所有的值都已经从“估计值”变为了“确定值”。

最终dis数组：

（这便是1号顶点到其余各个顶点的最短路径）.

基本思想：

每次找到离源点（上面例子的源点就是1号顶点）最近的一个顶点，然后以该顶点为中心进行扩展，最终得到源点到其余所有点的最短路径。基本步骤如下：

（1）将所有的顶点分成两部分：已知最短路程的顶点集合P和未知最短路径的顶点集合Q。最开始，已知最短路径的顶点集合P中只有源点一个顶点。我们这里用一个book数组来记录哪些点在集合P中。例如对于某个顶点i，如果book[i]为1则表示这个顶点在集合P中，如果book[i]为0则表示这个顶点在集合Q中。

（2）设置源点s到自己的最短路径为0即dis[s] = 0。若存在有源点能直接到达的顶点i，则把dis[i]设为e[s][i]。同时把所有其他（源点不能直接到达的）顶点的最短路径设为oo 。

（3）在集合Q的所有顶点中选择一个离源点s最近的顶点u（即dis[u]最小）加入到集合P。并考察所有以点u为起点的边，对每一条边进行松弛操作。例如存在一条从u到v的边，那么可以通过将边u-->v添加到尾部来拓展一条s到v的路径，这条路径的长度是dis[u] + e[u][v]。如果这个值比目前已知的dis[v]的值要小，我们可以用新值来替代当前dis[v]中的值。

（4）重复第三步，如果集合Q为空，结束。最终dis数组中的值就是源点到所有顶点的最短路径。

算法核心代码：

//Dijkstra算法核心语句for(i = 1 ; i <= n ; i ++){//找到离1号顶点最近的顶点min = inf;for(j = 1 ; j <= n ; j ++){if(book[j] == 0 && dis[j] < min){min = dis[j];u = j;}} book[u] = 1;for(v = 1 ; v <= n ; v ++){if(e[u][v] < inf){if(dis[u] + e[u][v] < dis[v])  dis[v] = dis[u] + e[u][v];}}}

算法完整代码：

#include<bits/stdc++.h>using namespace std;int e[10][10],dis[10],book[10];int main()
{int i,j;int n,m;int t1,t2,t3;int u,v,min;int inf = 99999999; //无穷//读入n和m，n表示顶点个数，m表示边的条数cin >> n >> m;//初始化for(i = 1 ; i <= n ; i ++){for(j = 1 ; j <= m ; j ++){if(i == j)  e[i][j] = 0;else  e[i][j] = inf;}}//读入边for(i = 1 ; i <= m ; i ++){cin >> t1 >> t2 >> t3;e[t1][t2] = t3;} //初始化dis数组，这里是1号顶点到其余各个顶点的初始路程for(i = 1 ; i <= n ; i ++)  dis[i] = e[1][i];//book数组初始化for(i = 1 ; i <= n ; i ++)  book[i] = 0;book[1] = 1;//Dijkstra算法核心语句for(i = 1 ; i <= n ; i ++){//找到离1号顶点最近的顶点min = inf;for(j = 1 ; j <= n ; j ++){if(book[j] == 0 && dis[j] < min){min = dis[j];u = j;}} book[u] = 1;for(v = 1 ; v <= n ; v ++){if(e[u][v] < inf){if(dis[u] + e[u][v] < dis[v])  dis[v] = dis[u] + e[u][v];}}}//输出最终的结果for(i = 1 ; i <= n ; i ++)  cout << dis[i] << ' ';getchar();getchar();return 0; 
}

通过上面的代码我们可以看出，这个算法的时间复杂度是O（N^2）。其中每次找到离1号顶点最近的顶点的时间复杂度是O（N），这里我们可以用“堆”来优化，使得这一部分的时间复杂度降低到O（logN）。另外对于边数M少了N^2的稀疏图来说（我们把M远小于N^2的图称为稀疏图，而M相较大的图成为稠密图），我们可以用邻接表代替邻接矩阵，使得整个时间复杂度优化到O（M + N）logN。请注意！在最坏的情况下M就是N^2，这样的话（M + N）logN要比N^2还要大。

用邻接表来存储一个图：

先上数据：