本文主要是介绍C++多线程下分别使用雅各比迭代法、高斯赛德尔迭代法、逐次超松弛迭代法解决稳态热传导问题,使用Python数据可视化,希望对大家解决编程问题提供一定的参考价值,需要的开发者们随着小编来一起学习吧!
稳态导热,稳态导热是物体的温度不随时间而变化的导热过程。稳态热传导问题在这里被模拟为,对于一个n*n的网格,对其某个位置持续给定初始温度,求解最终的稳态导热状态,稳态热传导问题即求解最终的稳态温度。
温度网格示例如下:

正确解决温度热传导问题后得到的温度图像类似于下图所示:
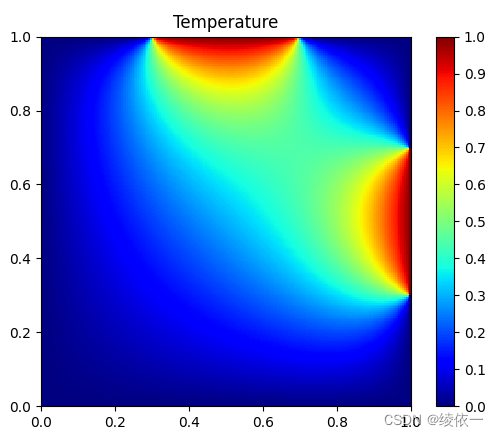
问题拟定
对于n*n的网格,初始温度全部为0,给其上边与右边的中部位置持续给定大小为1的热度,使用不同的方法求解最终的稳态导热状态,这里温度的变化模拟为上下左右四个点的平均值,并且考虑如何对稳态热传导求解过程进行并行化加速。
拟定方法
雅克比迭代法:雅克比迭代法是众多迭代法中比较早且较简单的一种,其命名也是为纪念普鲁士著名数学家雅可比。雅克比迭代法的计算公式简单,每迭代一次只需计算一次矩阵和向量的乘法,且计算过程中原始矩阵A始终不变,比较容易进行计算。然而这种迭代方式收敛速度较慢,而且占据的存储空间较大,所以工程中一般不直接用雅克比迭代法,而用其改进方法。
高斯消元法:是线性代数中学过的线性方程组求解的一个经典算法,通过把系数矩阵转化为行阶梯形矩阵去求解。该方法以数学家卡尔·高斯命名,但最早出现于《九章算术》。
逐次超松弛迭代法:D. M. Young于20世纪70年代提出逐次超松弛(Successive Over Relaxation)迭代法,简称SOR方法,是一种经典的迭代算法。它是为了解决大规模系统的线性等式提出来的,在GS法基础上为提高收敛速度,采用加权平均而得到的新算法。由于超松弛迭代法公式简单,编制程序容易,很多工程学、计算数学中都会应用超松弛迭代方法。使用超松弛迭代法的关键在于选取合适的松弛因子,如果松弛因子选取合适,则会大大缩短计算时间。
由于每个点的温度都为其周围四个点的平均值,因此对于每一个点来说都能写成uij =
1/4(ui-1,j + ui+1,j + ui,j-1 + ui,j+1),所以可以使用Au = b来求解,其中A为N^2*N^2的矩阵。使用并行的雅克比迭代法、高斯赛德尔迭代法和逐次超松弛迭代法解决稳态热传导问题,并对实验结果进行分析。
【系统设计】
设计思想
雅克比迭代法
方法设计:
1、将所有变元注意用其余变元表示
2、为所有变元指定初始值,开始迭代,每次迭代的计算次数相同,为变元总数
3、每次迭代结束后,检查本次迭代前后所有变元变化量的最大值,若小于设定的容差,那么迭代结束,输出结果。
加速设计:
雅克比迭代法每次迭代都会对温度网格进行遍历,在这里可以使用多线程执行这个过程。
高斯赛德尔迭代法
在前面的实验已经进行过高斯消元法的代码编写,对于这一题而言,对比雅克比法和高斯赛德尔法,雅克比迭代法没有用到当前迭代已解的数据,而高斯赛德尔迭代法用到了当前已经解的数据,因此相比较于雅克比迭代法,理论上高斯赛德尔迭代法会更快收敛。
逐次超松弛迭代法
逐次超松弛迭代法的主要思想就是在高斯赛德尔迭代法的基础之上增加一个松弛因子w,以此来达到更快速的收敛的目的,不过松弛因子一般并不好确定,所以需要进行试算。
详细设计
网格的初始化
首先是对于网格的初始化,初始化n*n的网格,然后设定初始温度。因为设计的是,将网格上边和右边中间三分之一的位置设定为1,因此判定n为3的倍数,同时网格数也不能太少,否则看起来就是几个像素块,这样能够对其,最后绘制的比较美观。然后就是对于tol阈值的选择,这里使用的是0.1/(n+1)^2。对于网格的创建,需要分配两个二维数组来存储,一个存储旧的温度,一个存储新的温度,新的温度网格由旧的温度网格来更新,更新完毕后将新的网格复制到旧的网格里。需要注意的是,对于网格的创建,不能只创建n*n大小,否则在迭代的时候会出现越界的情况,需要进行边界延拓。另外由于是指针创建的动态二维数组,在复制的时候不能仅仅使用等于号,而是需要遍历对指针的内容进行修改,否则等于号会直接修改同时两个网格。
部分相关代码:
double tol = 0.1 / (((double)n + 1) * ((double)n + 1)); // 阈值
double** old_temp = new double* [n + 2]; // 创建新旧温度网格
double** new_temp = new double* [n + 2];
// 创建时需要边界延拓
for (int i = 0; i < n + 2; i++) {old_temp[i] = new double[n + 2];new_temp[i] = new double[n + 2];for (int j = 0; j < n + 2; j++) {old_temp[i][j] = 0;new_temp[i][j] = 0;}
}
// 上边与右边中部温度初始化为1
void InitTemp(double** temp, int n) {for (int i = n / 3 + 1; i <= 2 * n / 3; i++) {temp[1][i] = 1;temp[i][n] = 1;}
}
雅克比迭代
主要是不断迭代检测变化的最大值和阈值的关系,同时为了避免一直迭代的情况需要设置一个迭代次数的最大值,所以结束迭代的方法有两种,一种是每轮迭代中变化的最大值比设定的阈值要小,还有就是达到了最大的迭代次数。因此迭代的框架如下:
while (maxiter > 0) {double max_dis = -1; // 每轮迭代变化的最大值if (max_dis > 0 && max_dis <= tol) { break; }todo: 更新新温度网格,max_dis=最大的变化值copy_grid(old_temp, new_temp, n); // 将旧的温度值更新maxiter--;
}
然后是对于新的温度网格的更新,这里模拟为上下左右四个点的温度的平均值,在每次更新的时候都比较一下变化量获得最大的变化量,需要注意的是对于温度源,设定是持续不断的温度为1的热源,因此更新的时候需要跳过热源。
// (i == 1) && (j >= n / 3 + 1) && (j <= 2 * n / 3) 这是上边界的温度源
// (i >= n / 3 + 1) && (i <= 2 * n / 3) && (j == n) 这是右边界的温度源
// 对于温度源需要跳过
if (!(((i == 1) && (j >= n / 3 + 1) && (j <= 2 * n / 3)) || ((i >= n / 3 + 1) && (i <= 2 * n / 3) && (j == n)))) {new_temp[i][j] = (old_temp[i - 1][j] + old_temp[i][j - 1] + old_temp[i + 1][j] + old_temp[i][j + 1]) / 4 + r;max_dis = _max(abs(new_temp[i][j] - old_temp[i][j]), max_dis);
}
但这样的代码得到的结果和预期并不相同,在打印结果数组的时候我发现网格最边缘的部分温度要比靠近内部的数值要小,分析后发现是因为在开始做边界延拓的时候,延拓的边界默认为0,在更新的时候也没有去修改,因此在整个迭代过程中一直为0,这就相当于给周围持续施加了一个冷却区域,因此在迭代的时候不仅仅需要修改内部网格的温度,对于周围的边界温度也需要修改,修改上下左右四边就是周围三点的平均值,四个顶点就是周围两个点的平均值,修改过程类似上一步。
经过上一步的代码修改,单从打印控制台查看数组已经是解决问题,输出符合期望。
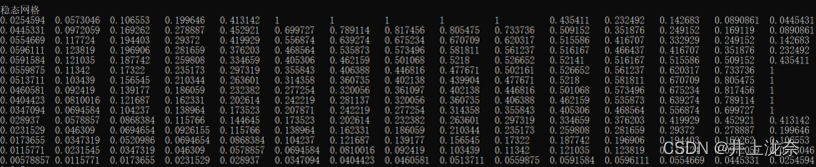
之后是使用openMP加速,首先在右键项目,在属性-配置属性-C/C++-语言中将支持openMP选择为是。
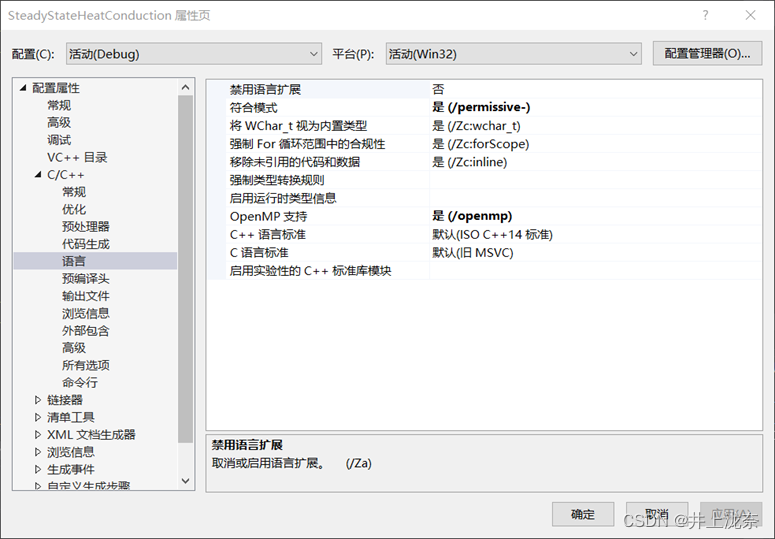
然后在要使用多线程的地方添加上openMP的注解,并指定线程数,如果不指定线程数那么openMP默认线程数为4。
#pragma omp parallel for num_threads(nthreads)
为确保结果正确,再次调用同样的函数确保多线程调用函数的输出没变,经观察确定打印输出结果和上一步单线程的输出是一样的,随后在主函数中调用并查看不同线程使用的时间。这里使用网格数为90,最大迭代次数为十万次示例。
int n = 90;
int maxiter = 100000;
double use_time;
clock_t startTime, endTime;
startTime = clock();
jacobi(n, maxiter,1); // 单线程
endTime = clock();
use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;
cout << "单线程用时:" << use_time << endl;
绘制热力图
对于热力图的绘制,c++并不是很好操作,这里在python中调用matplotlib库和seaborn库来进行绘制,这样需要将c++中网格的输出结果链接到python中,比较简单的方式就是通过txt来链接,c++负责处理网格数据并写入文本文件,python读取文本文件后调用seaborn库中的heatmap函数来绘制热力图。
c++需要写入的数据有网格的大小和网格的数据,为了二后续更方便的操作,这里写入两个文件,一个存储网格数据,每一个数据存储一行,另一个文件为网格的大小(也可以直接对网格数据的len进行开方),三种迭代方式的通用网格大小可以在指定函数之前解写入,需要注意的是写入之前需要设置覆盖文件内容而不是在源文件后追加内容,否则一是一维数组转二维数组的时候会大小不匹配,二是就算碰巧转置了绘制的热力图也是错误的。
string path = "D:\\Project\\PycharmProjects\\DrawMatrixThermodynamicDiagram\\";
path += file_name + ".txt";
fstream fout(path, ios::out | ios::binary);
for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {fout << temp[i][j] << endl;}
}
在python中首先读取数据,使用numpy的loadtxt库,读取的网格数据为一维数组,然后根据读取的维度大小,使用reshape函数将一维数组转化为n*n的二维数组,然后使用heatmap函数绘制热力图,需要注点将annot设置为false,否则网格上会有每个网格块的数值,Linewidth也要设置为0,否则每个网格块会有白色的边缘线。
def loadtxt(filename):read_data = np.loadtxt(filename, dtype=np.float32) # 读取网格数据dimension = np.loadtxt("dimension.txt", dtype=np.int64) # 读取网格大小result = read_data.reshape((dimension, dimension)) # 将一维数据转为二维return resultdata = loadtxt('jacobi.txt')
plt.subplots(figsize=(5, 5))
plt.title("jacobi")
sns.heatmap(data,square=True,annot=False,yticklabels=False,xticklabels=False,linewidth=0.0,cmap=cm.get_cmap("jet"))
plt.rc('font', family='Times New Roman')
plt.tight_layout()
plt.show()
高斯赛德尔迭代
高斯消元法实际并不复杂,主要步骤就是消元和回代两个过程。消元:通过行变换将下三角矩阵变为0;回代:根据消元所得到的的上三角矩阵通过回代法求解方程组的解。
消元过程有特定的公式,对于要消除的元素aij,对应的操作为:
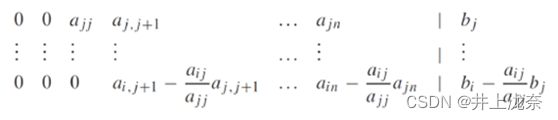
最后通过公式计算每一项的值:

对于高斯赛德尔和雅克比的比较:
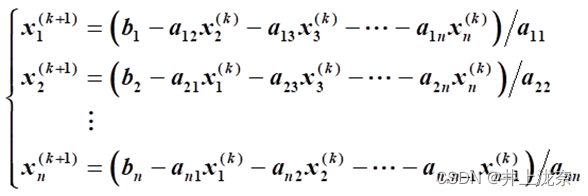
雅克比迭代公式
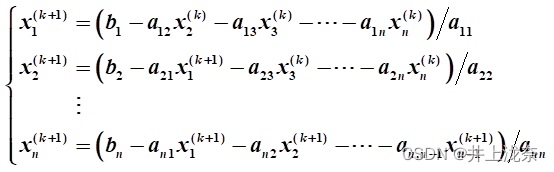
高斯赛德尔迭代公式
通过上面的公式可以看出,高斯赛德尔迭代即在雅克比迭代的基础上,在计算xi^(k+1)用已经算出来的x1^(k+1),…,xi-1^(k+1)替换x1^(k),…,xi-1^(k)。
对于本次实验,相比于雅克比迭代法,高斯赛德尔能够运用到刚得到的解,因此不需要像雅克比方法一样使用两个数组new和old来存储新旧数据,可以直接使用一个数组存储得到的数据,能够更快地达到结果收敛的目的,需要注意使用临时变量存储更新前的变量以便做差值计算,总体来说就是在雅克比迭代法的基础之上做一些修改即可。
if (i >= 1 && i <= n && j >= 1 && j <= n) {if (!(((i == 1) && (j >= n / 3 + 1) && (j <= 2 * n / 3)) || ((i >= n / 3 + 1) && (i <= 2 * n / 3) && (j == n)))) {double temp = temperature[i][j];temperature[i][j] = (temperature[i - 1][j] + temperature[i][j - 1] + temperature[i + 1][j] + temperature[i][j + 1]) / 4 + r;max_dis = _max(abs(temp - temperature[i][j]), max_dis);}
}
从控制台打印大小较小的网格运行效果,可以看到结果是符合预期的:

多线程加速类似雅克比迭代法,通过同样的网格大小调用不同的线程数统计时间,和雅克比迭代法法比较可以发现高斯赛德尔法加速效果十分明显。
逐次超松弛迭代
对于高斯赛德尔迭代法:

令
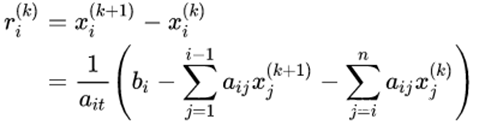
有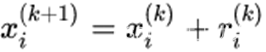
在改变量r前加一个因子w得到
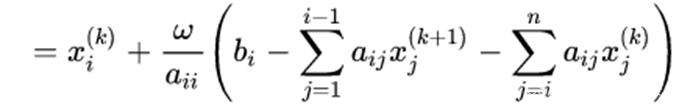
逐次超松弛迭代法是在高斯赛德尔迭代法的基础上增加一个松弛因子w(0 < w < 2),如果松弛因子选择合理,则逐次超松弛迭代法能够更快收敛,不过一般松弛因子选择比较困难,因此需要进行试算。
if (!(((i == 1) && (j >= n / 3 + 1) && (j <= 2 * n / 3)) || ((i >= n / 3 + 1) && (i <= 2 * n / 3) && (j == n)))) {double temp = temperature[i][j];temperature[i][j] = (temperature[i - 1][j] + temperature[i][j - 1] + temperature[i + 1][j] + temperature[i][j + 1]) / 4;max_dis = _max(abs(temp - temperature[i][j]), max_dis);temperature[i][j] += w * abs(temp - temperature[i][j]);
}由于w需要试算,在w的取值范围内,以0.1为步长,不断循环来寻找最佳的w值。
for (double i = 0; i < 2; i += 0.1) {double use_time;clock_t startTime, endTime;startTime = clock();sor(n, maxiter, 4, i);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "w = " << i << "用时:" << use_time << endl;
}
可以看到在w小于1的时候加速效果十分明显,w = 0.8的时候最快(0的时候因为松弛因子范围非法所以后面的函数没有执行而是直接返回),而当松弛因子为1的时候即为高斯赛德尔迭代法(网格大小为90*90,最大迭代次数为10万,线程数为4),松弛因子大于1的时候加速效果不是特别明显。
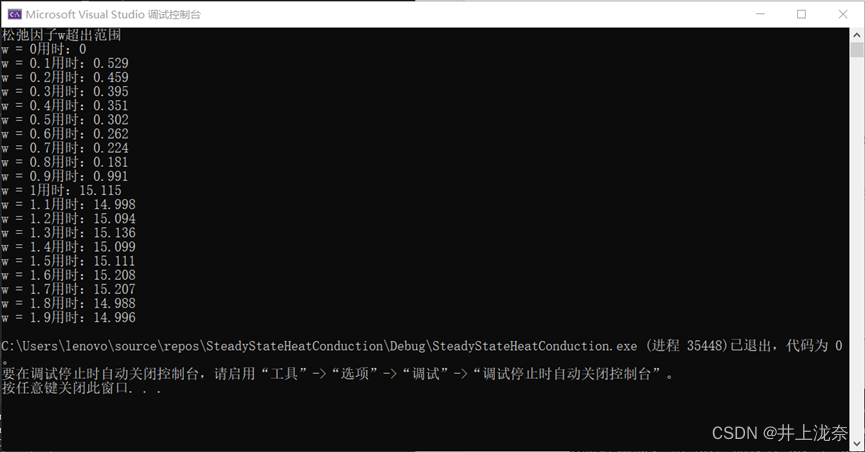
因此后面多线程效率测试以及绘制热力图的w选择均为0.8。
运行效率比较
雅克比迭代
在90*90的网格,最大迭代十万次下,不同线程花费时间(单位:s)

在150*150的网格,最大迭代十万次下,不同线程花费时间(单位:s)

绘制热力图(网格大小300*300,最大迭代10万次,数据处理四线程下花费2442.41s)
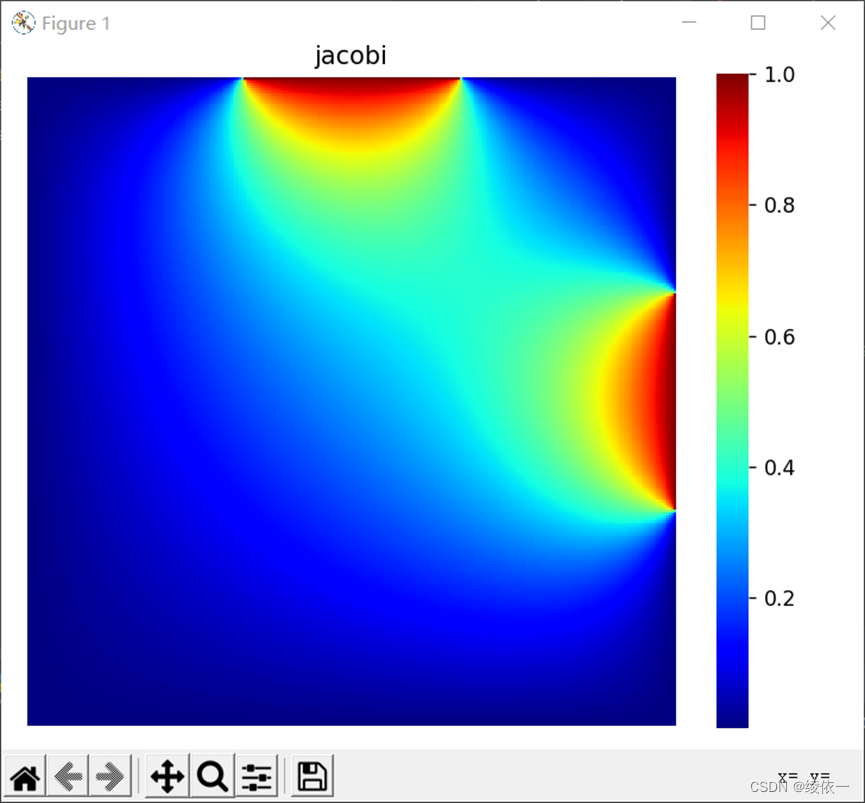
高斯赛德尔迭代
在90*90的网格,最大迭代十万次下,不同线程花费时间(单位:s)

在150*150的网格,最大迭代十万次下,不同线程花费时间(单位:s)

绘制热力图(网格大小300*300,最大迭代10万次,数据处理四线程下花费357.805s)

逐次超松弛迭代
在90*90的网格,最大迭代十万次下,不同线程花费时间(单位:s)

在150*150的网格,最大迭代十万次下,不同线程花费时间(单位:s)

在300*300的网格,最大迭代十万次下,不同线程花费时间(单位:s)

绘制热力图(网格大小300*300,最大迭代10万次,数据处理四线程下花费10.209s)
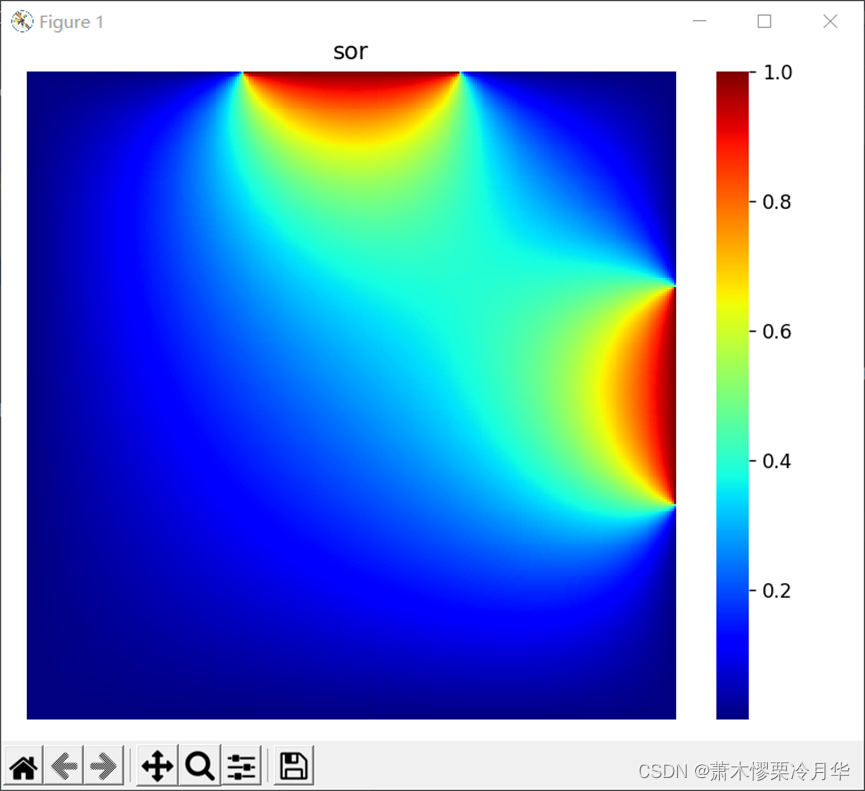
绘制热力图(网格大小600*600,最大迭代10万次,数据处理四线程下花费168.687s)
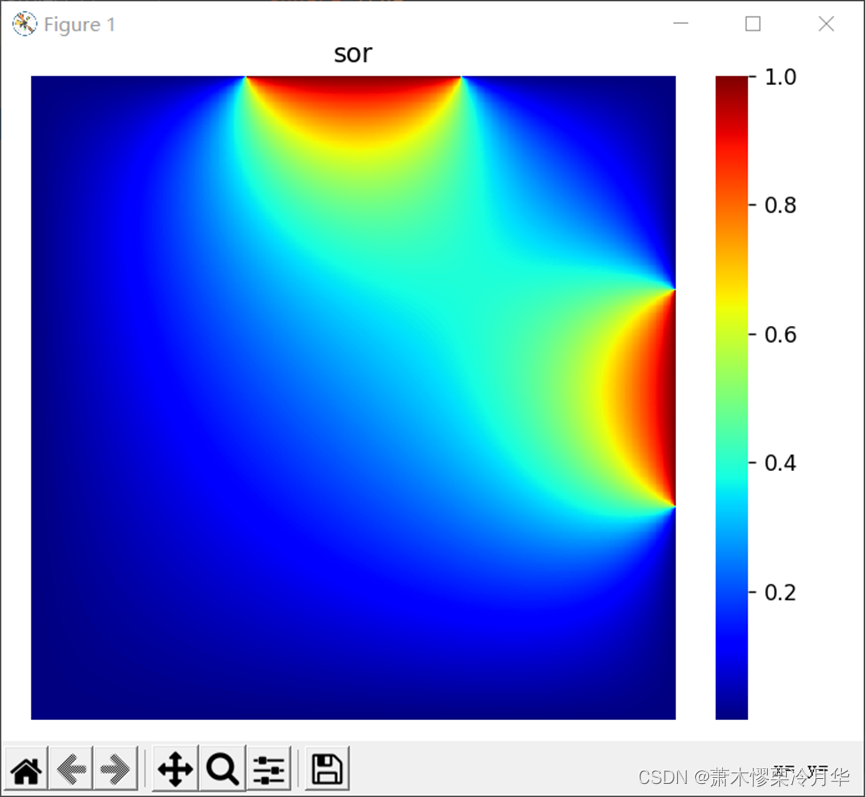
综合比较
c++代码部分,计算矩阵结果
SOR.h
#pragma once
#include"functions.h"
#include"omp.h"void sor(int n, int maxiter, int nthreads, double w) {if (n < 6) {cout << "网格数太少" << endl;return;}if (n % 3 != 0) {cout << "网格数应为3的倍数" << endl;return;}if (w <= 0 || w >= 2) {cout << "松弛因子w超出范围" << endl;return;}double tol = 0.1 / (((double)n + 1) * ((double)n + 1)); // 阈值double** temperature = new double* [n + 2];for (int i = 0; i < n + 2; i++) {temperature[i] = new double[n + 2];for (int j = 0; j < n + 2; j++) {temperature[i][j] = 0;}}InitTemp(temperature, n);if (n <= 15) {cout << "初始化网格" << endl;print_temp(temperature, n);}while (maxiter > 0) {double max_dis = -1;#pragma omp parallel for num_threads(nthreads)for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (!(((i == 1) && (j >= n / 3 + 1) && (j <= 2 * n / 3)) || ((i >= n / 3 + 1) && (i <= 2 * n / 3) && (j == n)))) {double temp = temperature[i][j];temperature[i][j] = (temperature[i - 1][j] + temperature[i][j - 1] + temperature[i + 1][j] + temperature[i][j + 1]) / 4;max_dis = _max(abs(temp - temperature[i][j]), max_dis);temperature[i][j] += w * abs(temp - temperature[i][j]);}}}if (max_dis > 0 && max_dis <= tol) {break;}maxiter--;}if (n <= 15) {cout << endl << "稳态网格" << endl;print_temp(temperature, n);}writeToTxt(temperature, n, "sor"); // 写入txt// 释放内存for (int i = 0; i < n + 2; i++) {delete[] temperature[i];}delete[] temperature;
}
Gauss.h
#pragma once
#include"functions.h"
#include"omp.h"void gauss(int n, int maxiter, int nthreads) {if (n < 6) {cout << "网格数太少" << endl;return;}if (n % 3 != 0) {cout << "网格数应为3的倍数" << endl;return;}double tol = 0.1 / (((double)n + 1) * ((double)n + 1)); // 阈值double** temperature = new double* [n + 2];for (int i = 0; i < n + 2; i++) {temperature[i] = new double[n + 2];for (int j = 0; j < n + 2; j++) {temperature[i][j] = 0;}}InitTemp(temperature, n);if (n <= 15) {cout << "初始化网格" << endl;print_temp(temperature, n);}while (maxiter > 0) {double max_dis = -1;#pragma omp parallel for num_threads(nthreads)for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {if (!(((i == 1) && (j >= n / 3 + 1) && (j <= 2 * n / 3)) || ((i >= n / 3 + 1) && (i <= 2 * n / 3) && (j == n)))) {double temp = temperature[i][j];temperature[i][j] = (temperature[i - 1][j] + temperature[i][j - 1] + temperature[i + 1][j] + temperature[i][j + 1]) / 4;max_dis = _max(abs(temp - temperature[i][j]), max_dis);}}}if (max_dis > 0 && max_dis <= tol) {break;}maxiter--;}if (n <= 15) {cout << endl << "稳态网格" << endl;print_temp(temperature, n);}writeToTxt(temperature, n, "gauss"); // 写入txt// 释放内存for (int i = 0; i < n + 2; i++) {delete[] temperature[i];}delete[] temperature;
}jacobi.h
#pragma once
#include"functions.h"
#include"omp.h"void jacobi(int n,int maxiter,int nthreads){if (n < 6) {cout << "网格数太少" << endl;return;}if (n % 3 != 0) {cout << "网格数应为3的倍数" << endl;return;}double tol = 0.1 / (((double)n + 1) * ((double)n + 1)); // 阈值double** old_temp = new double* [n + 2]; // 创建新旧温度网格double** new_temp = new double* [n + 2];// 创建时需要边界延拓for (int i = 0; i < n + 2; i++) {old_temp[i] = new double[n + 2];new_temp[i] = new double[n + 2];for (int j = 0; j < n + 2; j++) {old_temp[i][j] = 0;new_temp[i][j] = 0;}}InitTemp(old_temp,n); // 初始化网格InitTemp(new_temp, n);if (n <= 15) {// 网格太大就不输出了cout << "初始化网格" << endl;print_temp(old_temp, n);}while (maxiter > 0) {double max_dis = -1; // 每轮迭代变化的最大值#pragma omp parallel for num_threads(nthreads)for (int i = 0; i <= n + 1; i++) {for (int j = 0; j <= n + 1; j++) {// 处理上边界if (i == 0) {for (int j = 1; j <= n; j++) {new_temp[i][j] = (old_temp[i][j - 1] + old_temp[i + 1][j] + old_temp[i][j + 1]) / 3;}}// 处理下边界else if (i == n + 1) {for (int j = 1; j <= n; j++) {new_temp[i][j] = (old_temp[i][j - 1] + old_temp[i - 1][j] + old_temp[i][j + 1]) / 3;}}// 处理左边界else if (j == 0) {for (int i = 1; i <= n; i++) {new_temp[i][j] = (old_temp[i - 1][j] + old_temp[i + 1][j] + old_temp[i][j + 1]) / 3;}}// 处理右边界else if (j == n + 1) {for (int i = 1; i <= n; i++) {new_temp[i][j] = (old_temp[i - 1][j] + old_temp[i + 1][j] + old_temp[i][j - 1]) / 3;}}else {// (i == 1) && (j >= n / 3 + 1) && (j <= 2 * n / 3) 这是上边界的温度源// (i >= n / 3 + 1) && (i <= 2 * n / 3) && (j == n) 这是右边界的温度源// 对于温度源需要跳过if (!(((i == 1) && (j >= n / 3 + 1) && (j <= 2 * n / 3)) || ((i >= n / 3 + 1) && (i <= 2 * n / 3) && (j == n)))) {new_temp[i][j] = (old_temp[i - 1][j] + old_temp[i][j - 1] + old_temp[i + 1][j] + old_temp[i][j + 1]) / 4;max_dis = _max(abs(new_temp[i][j] - old_temp[i][j]), max_dis);}}// 处理四个顶点new_temp[0][0] = (old_temp[1][0] + old_temp[0][1]) / 2;new_temp[0][n + 1] = (old_temp[1][n + 1] + old_temp[0][n]) / 2;new_temp[n + 1][0] = (old_temp[n + 1][1] + old_temp[n][0]) / 2;new_temp[n + 1][n + 1] = (old_temp[n + 1][n] + old_temp[n][n + 1]) / 2;}}if (max_dis > 0 && max_dis <= tol) {break;}copy_grid(old_temp, new_temp, n); // 将旧的温度值更新maxiter--;}if (n <= 15) {cout << endl << "稳态网格" << endl;print_temp(new_temp, n);}writeToTxt(new_temp, n, "jacobi"); // 写入txt// 释放内存for (int i = 0; i < n + 2; i++) {delete[] old_temp[i];delete[] new_temp[i];}delete[] old_temp;delete[] new_temp;
}functions.h
#pragma once
#include<iostream>
#include <iomanip>
#include <fstream>
using namespace std;double _max(double a, double b) {return a > b ? a : b;
}void InitTemp(double** temp, int n) {for (int i = n / 3 + 1; i <= 2 * n / 3; i++) {temp[1][i] = 1;temp[i][n] = 1;}
}void copy_grid(double** grid1, double** grid2, int n) {for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {grid1[i][j] = grid2[i][j];}}
}void print_temp(double** temp, int n) {for (int i = 0; i <= n+1; i++) {for (int j = 0; j <= n+1; j++) {cout << left << setw(10) << temp[i][j] << " ";}cout << endl;}
}void writeToTxt(double** temp, int n, string file_name) {string path = "D:\\Project\\PycharmProjects\\DrawMatrixThermodynamicDiagram\\";path += file_name + ".txt";fstream fout(path, ios::out | ios::binary);for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {fout << temp[i][j] << endl;}}
}void writeDimension(int n) {string path = "D:\\Project\\PycharmProjects\\DrawMatrixThermodynamicDiagram\\dimension.txt";fstream fout(path, ios::out | ios::binary);fout << n << endl;
}
EfficiencyCompare.h
#pragma once
#include"Jacobi.h"
#include"Gauss.h"
#include"SOR.h"void jacobi_efficiency(int n, int maxiter) {double use_time;clock_t startTime, endTime;double one_time = 0;// 单线程startTime = clock();jacobi(n, maxiter, 1);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;one_time = use_time;cout << "单线程用时:" << use_time << endl;// 双线程startTime = clock();jacobi(n, maxiter, 2);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "双线程用时:" << use_time << ",加速比为:" << one_time / use_time << endl;// 4线程startTime = clock();jacobi(n, maxiter, 4);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "4线程用时:" << use_time << ",加速比为:" << one_time / use_time << endl;// 6线程startTime = clock();jacobi(n, maxiter, 6);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "6线程用时:" << use_time << ",加速比为:" << one_time / use_time << endl;// 12线程startTime = clock();jacobi(n, maxiter, 12);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "12线程用时:" << use_time << ",加速比为:" << one_time / use_time << endl;
}void gauss_efficiency(int n, int maxiter) {double use_time;clock_t startTime, endTime;double one_time = 0;// 单线程startTime = clock();gauss(n, maxiter, 1);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;one_time = use_time;cout << "单线程用时:" << use_time << endl;// 双线程startTime = clock();gauss(n, maxiter, 2);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "双线程用时:" << use_time << ",加速比为:" << one_time / use_time << endl;// 4线程startTime = clock();gauss(n, maxiter, 4);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "4线程用时:" << use_time << ",加速比为:" << one_time / use_time << endl;// 6线程startTime = clock();gauss(n, maxiter, 6);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "6线程用时:" << use_time << ",加速比为:" << one_time / use_time << endl;// 12线程startTime = clock();gauss(n, maxiter, 12);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "12线程用时:" << use_time << ",加速比为:" << one_time / use_time << endl;
}void sor_efficiency(int n, int maxiter, double w) {double use_time;clock_t startTime, endTime;double one_time = 0;// 单线程startTime = clock();sor(n, maxiter, 1, w);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;one_time = use_time;cout << "单线程用时:" << use_time << endl;// 双线程startTime = clock();sor(n, maxiter, 2, w);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "双线程用时:" << use_time << ",加速比为:" << one_time / use_time << endl;// 4线程startTime = clock();sor(n, maxiter, 4, w);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "4线程用时:" << use_time << ",加速比为:" << one_time / use_time << endl;// 6线程startTime = clock();sor(n, maxiter, 6, w);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "6线程用时:" << use_time << ",加速比为:" << one_time / use_time << endl;// 12线程startTime = clock();sor(n, maxiter, 12, w);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "12线程用时:" << use_time << ",加速比为:" << one_time / use_time << endl;
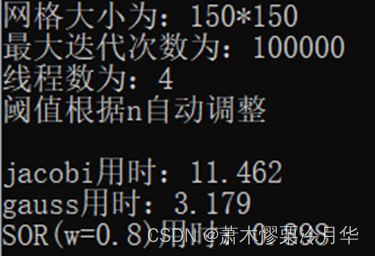
}void compare(int n, int maxiter, int nthreads) {cout << "网格大小为:" << n << "*" << n << endl;cout << "最大迭代次数为:" << maxiter << endl;cout << "线程数为:" << nthreads << endl;cout << "阈值根据n自动调整" << endl << endl;double w = 0.8;double use_time;clock_t startTime, endTime;double one_time = 0;startTime = clock();jacobi(n, maxiter, 4);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "jacobi用时:" << use_time << endl;startTime = clock();gauss(n, maxiter, 4);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "gauss用时:" << use_time << endl;startTime = clock();sor(n, maxiter, nthreads, w);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "SOR(w=0.8)用时:" << use_time << endl;
}source.cpp
#include"EfficiencyCompare.h"int main() {int n = 150;int maxiter = 100000;int nthreads = 4;writeDimension(n);各自线程比较//jacobi_efficiency(n, maxiter);//cout << endl;//gauss_efficiency(n, maxiter);//cout << endl;//sor_efficiency(n, maxiter, 0.8);compare(n, maxiter, nthreads);/*double use_time;clock_t startTime, endTime;startTime = clock();sor(n, maxiter, 4, 0.8);endTime = clock();use_time = ((double)endTime - (double)startTime) / CLOCKS_PER_SEC;cout << "用时:" << use_time << endl;*/
}python部分代码,数据可视化
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
from matplotlib import cmdef loadtxt(filename):read_data = np.loadtxt(filename, dtype=np.float32) # 读取网格数据dimension = np.loadtxt("dimension.txt", dtype=np.int64) # 读取网格大小result = read_data.reshape((dimension, dimension)) # 将一维数据转为二维return resultdef draw_map(filename):file = filename + '.txt'data = loadtxt(file)plt.subplots(figsize=(5, 5))plt.title(filename)sns.heatmap(data,square=True,annot=False,yticklabels=False,xticklabels=False,linewidth=0.0,cmap=cm.get_cmap("jet"))plt.rc('font', family='Times New Roman')plt.tight_layout()plt.show()if __name__ == "__main__":# draw_map("jacobi")# draw_map("gauss")draw_map("sor")
这篇关于C++多线程下分别使用雅各比迭代法、高斯赛德尔迭代法、逐次超松弛迭代法解决稳态热传导问题,使用Python数据可视化的文章就介绍到这儿,希望我们推荐的文章对编程师们有所帮助!



